Strukturované programování

Dušan Polanský

Strukturované programování bylo koncem 70. a v 80. letech programátorskou hitovkou. Hodně bylo propagováno pod praporem programovacího jazyka Pascal, protože ten byl navržen a implementován tak, aby tento styl programování přirozeně podporoval. V té době většině ostatních jazyků tahle vlastnost dost chyběla. Dnes většina jazyků tenhle způsob programování podporuje, ovšem Pascal má jednu výhodu dodnes, kvůli své jednoduchosti, jasnosti, koncepčnosti, čitelnosti zdrojového kódu se výborně hodí, mimo jiné, na výuku algoritmizace, programovacích technik, překladačů a pochopitelně i strukturovaného programování. I proto je dodnes (text píšu v roce 2012) využíván ve výuce na středních a vysokých školách.

Základní myšlenka strukturovaného programování je zdánlivě velmi přirozená a jednoduchá: při tvorbě algoritmu a programu postupuj shora dolů, maximálně se drž abstraktního přístupu, používej jenom tři základní řídicí struktury: sekvenci, selekci (větvení) a opakování; a detailni definici datových struktur odkládej až do té doby, dokud ji nepoužiješ při zápisu programového kódu. Teoreticky bychom neměli používat příkaz skoku (goto). V některých povídáních o strukturovaném programování -- jakási praktická bible k tomuto stylu programování nebyla zatím napsána, i když knih a různých pseudočlánků habaděj :-) -- se proto autoři tomuto příkazu halasně vyhýbají, málem jako alkoholik limonádě. V reálných větších projektech se tomuto příkazu vyhnout nemusí být až tak jednoduché a už vůbec neznamená, že použití tohoto příkazu je automatickou negací strukturovaného programování. Pochopitelně ale i zde platí, že všeho s mírou.

Postup shora dolů a datovou abstrakci běžně v životě používáme všichni. Pokud sníte o hezkém domě, asi si prvně nepředstavujete jaké budete mít kliky na oknách (i když u žen platí, že prioritně řeší vzor a barvu kachliček v koupelně a na toaletě, ale každá výjimka potvrzuje pravidlo), ale nejdřív vidíte celý dům postaven jaksi abstraktně, virtuálně, ve svých představách. Teprve pak začnete své představy zpřesňovat, řešíte detailně uspořádní místností atd. No a kdesi na konci se dostanete i k těm klikám na oknech. Na kliku jsem si vzpomněl proto, že moje malá vnučka, když ji držím u okna a spolu se smutně díváme na nehezký panelák naproti našemu stejně nehezkému, jenž nám brání výhledu na les, zuřivě začně lomcovat klikou, která se ji ale dost nešikovně drží, neboť je krátká. V programátorské praxi tohle tlachání znamená: příslušný detail řešíme, až když není vyhnutí. Jinak o postupu shora dolů se někdy říká, že program tvoříme po vrstvách; shora dolů se mi ale líbí více. Proč tomu tak je, jsme již poznali na stavbě rodinné vily. Teď si jenom zapamatujeme, že barvu a velikost kachliček v koupelně řešíme, až když koupelna stojí, nebo těsně před jejím dohotovením. Ale vilu stavět nebudeme, raději si dáme nějaký teoretický příklad.

Ten jsem nevymyslel, protože na to jednoduše nemám. Převzal jsem jej z knihy, kterou jsem již dávno dávno prodal, vydalo ji v roce 1979 SNTL, Praha, autor je Per Brich Hansen a jmenuje se Principy operačních systémů. Čtenářům bych ještě doporučil knihu od českého autora: Tomáš Hruška, Pascal pro začátečníky, je z roku 1989 a rovněž ji vydalo SNTL. Autor ve výkladu ani v příkladech nepoužívá příkaz goto. Knihu jsem již kdysi měl, pak nenávratně komusi půjčil, ale štěstí mi nedávno přálo, při vyhazování odpadků jsem knihu zmerčil v kontajneru, zalovil jsem rukou, doma ji zdezinfikoval, jelikož byla chuděra jakási poničená a něčím polita. Je napsaná opravdu svěže a na vysoké metodické úrovni. Autor sice nepracuje s databázemi, ale pro pochopení základů strukturovaného programování to není až tak stěžejní.

Program jsem odladil v Turbo Pascalu, Version 7.0, tahle verze je z roku 1992. Určitě se mladí guráci teď chechtají, ale jelikož mně bude za pár měsíců šedesát, tak to beru s nadhledem. Pro ně mohu doporučit k stažení free vývojové prostředí Lazarus, které obsahuje Free Pascal. V každém případě na praktickou ukázku strukturovaného programování oba překladače jsou až až. Zdroják k stažení nedávám, koneckonců není problém si zdrojový kód zkopírovat, ale pokud si stáhnete zdroják a sami si program lopotně postupně nevytvoříte, tak jak si to za chvíli ukážeme, tak je vám tohle povídání k ničemu, maximálně můžete o tom učeně žvanit u kofoly. V mé oblíbené vinotéce ale těžko, tam se věkový průměr štamgastů pohybuje kolem šedesáti let, a ti se rohlíkem, natož kofolou, opít nedají.

Po úvodu dlouhém jako fronta okradených klientů u právě vytunelované banky se dáme do práce. Napíšeme si zadání a pak bude postupovat strukturovaně krůček po krůčku k vytouženému cíli: k ne zcela triviálnímu strukturovanému programu.

Na jednoduchých situacích si ukážeme, co vlastně budeme od našeho programu chtít. Pro snadnější pochopení problému budeme uvažovat pouze jednu měnu a tři zákazníky, program ale napíšeme tak, aby pracoval s konečným počtem měn a zákazníků, ale to na samotné logice algoritmu již nic podstatného nezmění. Takže příklad na dvě situace, jedna bude jistá, druhá nejistá.

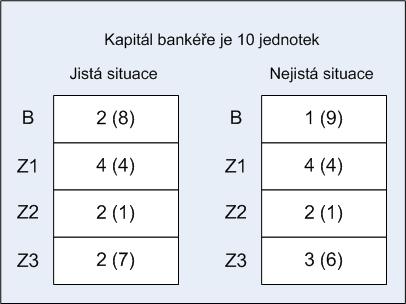
K první situaci. Bankéř má dispoziční hotovot 2 peněžní jednotky, 8 jednotek již zapůjčil. U zákazníka první číslo uvádí již vypůjčenou částku, druhé počet jednotek potřebných k dokončení transakce, tj. požadavek zákazníka na bankéře. Ten postupně analyzuje požadavky všech zákazníků v pořadí Z1, Z2, Z3. Z1 nemůže zapůjčit, neboť jeho požadavek převyšuje jeho dispoziční hotovost. Z2 půjčí jednu jednotku, ten transakci dokončí a vrátí bankéři 3 jednotky. Teď má bankéř dispoziční hotovost 4 jednotky. Z3 nemůže stále zapůjčit, tak se vrátí k Z1, tomu zapůjčí 4 jednotky. Z1 dokončí transakci a vrátí mu 8 jednotek, což bankéři umožní zapůjčit i Z3. Ten po dokončení transakce mu vrátí 9 jednotek a bankéř na konci všech transakcí si přijde opět na své, tj. má 10 jednotek. První případ je jistou situaci. Situace na druhém obrázku je jasně nejistá. Bankéř Z2 půjčí 1 jednotku, ten mu sice vrátí 3, ale další zákazníci požadují 4 nebo 6 jednotek, ale ty k dispozici nemá.

První krok, současně i nejvyšší úroveň abstrakce datových struktur:

type S=?
function jisty(beznystav:S): boolean;

Od funkce jisty požadujeme, aby nám zjistila, zda je situace z pohledu bankéře jistá nebo nejistá. Na téhle úrovni abstrakce ještě není nutné definovat datový typ popisující výchozí situaci, neboť s žádnou proměnnou datového typu S zatím algoritmus nepracuje.

V druhém kroku sestoupíme o kousek níž.

function jisty(beznystav:S): boolean;
var stav: S;
begin {jisty}
 stav:= beznystav;
 doktrans(stav);
 jisty:=vsetrdok(stav);
end;  {jisty}

Zde již musíme deklarovat proměnnou stav typu S. Proč? Protože jsme ji použili coby vstupní parametr v proceduře doktrans a logické funkci vsetrdok. Procedura doktrans (testování dokončení všech transakcí jednoho zákazníka) postupně zjistí situaci každého zákazníka a otestuje zda je možné dokončit všechny jeho transakce. V případě že ano, tak zákazník vrátí zapůjčené částky peněz v příslušných měnách bankéři. Funkce vsetrdok (testování dokončení všech transakcí všech zákazníků) jenom otestuje, zda pro všechny měny je výchozí kapitál bankéře roven hotovosti, kterou bude mít na konci k dispozici. Pokud ne, je situace nejistá a bankéř přišel o kapitál. Pokud ano, transakce všichni zákazníci dokončí, vrátí mu zapůjčené peníze a z pohledu bankéře je situace jistá.

V třetím kroku vyřešíme proceduru doktrans(stav):

Procedura doktrans bude procházet v opakovaných cyklech (teoreticky za určité situace může stačit jeden jediný průchod všemi zákazníky) postupně všechny zákazníky, zjistí zda je možné uspokojit požadavek některého zákazníka na všechny měny, pokud ano, tak mu požadovanou částku zapůjčí, pokud ne, tak si jenom poznačí, že zatím uspokojení požadavku není možné. Procedura bude zákazníky procházet opakovaně do té doby, než bankéři alespoň jeden zákazník vrátí zapůjčené částky v příslušných měnách nebo bankéř zkonstatuje, že ještě některá nebo některé transakce jsou nedokončeny, ale on přitom nemá dostatečnou hotovost, aby aspoň jednu transakci dokončil. Pro napsání této procedury již budeme muset definovat typ S, případně i jiné typy vyvolané potřebou definovat typ S. Takže se o to pokusíme.

type
 B = 1..poczakaz;
 D = 1..pocmen;
 H = array [D] of integer;
 S = record
       transakce: array [B] of
          record
              pozadavek,pujcka: H;
              dokonceno: boolean;
          end;
       kapital,hotovost: H;
     end;

Datový typ S není žádný jednoduchý typ, i když z pohledu našeho problému je definovaný velmi přirozeně. Zkuste si jej názorně nakreslit. Horní mez počtu měn pocmen jsme zatím ještě nemuseli definovat, ale zase proč ne již teď, když se doslova nabízí jako na podnosu. Než začneme tuhle nejtěžší proceduru psát, nakreslíme si její finální vývojový diagram. Použili jsme v něm, mimo jiné, i proměnnou datového typu boolean pokracuj. K čemu? Zajišťuje nám, že budeme všechny zákazníky opět a opět procházet do té doby, než bankéř bude mít jistotu, že je možné dokončení další transakce některého zákazníka. Ten mu vrátí zapůjčené peníze v příslušných měnách a on se bude moci pokusit zapůjčit peníze dalšímu zákazníkovi. Pokud již takový případ nenastane, tak se neprovede příkaz pokracuj := true a z koloběhu opakovaných cyklů přes všechny zákazníky unikneme pomocí podmínky until (not pokracuj).

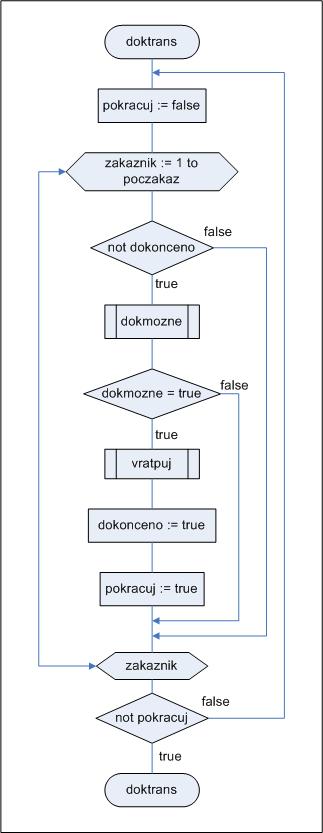
A nynčko, jak by napsal K. J. Erben ve svých pohádkách, můžeme přistoupit k napsání zdrojového textu procedury doktrans(stav).

procedure doktrans(var stav: S);
 var zakaznik: B; pokracuj: boolean;
 begin {doktrans}
 with stav do
  repeat
   pokracuj := false;
   for zakaznik := 1 to poczakaz do
    with transakce[zakaznik] do
    if (not dokonceno)  then
    if (dokmozne(pozadavek,hotovost)) then
         begin
          vratpuj(pujcka,hotovost);
          dokonceno := true;
          pokracuj := true;
         end
  until (not pokracuj);
 end; {doktrans}

Zatím jsme nerozpracovali, v souladu se zásadami strukturovaného programování, funkci dokmozne(pozadavek, hotovost) a proceduru vratpuj(pujcka,hotovost). To učiníme v dalších dvou krocích.

Čtvrtý krok, funkce dokmozne(pozadavek,hotovost):

Funkce dokmozne(pozadavek,hotovost) je relativně jednoduchá. Zjistí pro konkrétního zákazníka pro každou měnu, zda bankéřova hotovost pokrývá požadavek zákazníka na určitou měnu. Pokud ano funkce vrátí true, pokud ne false. Zde již musíme deklarovat proměnnou typu D, která nám říká, s kolika měnami se pracuje, neboť budeme používat cyklus for mena := 1 to pocmen do. My jsme si typ D definovali trochu předčasně již výše.

function dokmozne(pozadavek,hotovost:H):boolean;
   label 11;
   var
    mena: D;
   begin {dokmozne}
    for mena := 1 to pocmen do
      if (pozadavek[mena] > hotovost[mena]) then
       begin
        dokmozne:=false;
        goto 11;
      end;
        dokmozne:=true;
    11:
   end; {dokmozne}

Zde jsme použili příkaz goto, který je v strukturovaném programování tak přísně teoretiky nedoporučován. Jeho použití je zde typické. Pokud u konkrétního zákazníka u některé měny zjistíme, že dokončení transakce není možné, předčasně ukončíme cyklus for právě pomocí příkazu goto, neboť je zbytečné testovat další měny. Jinak pro předčasné ukončení cyklu Pascal nabízí příkaz break. A ještě přidáme trochu teorie strukturovaného programování, podle ní každý podprogram (v Pascalu procedura nebo funkce) by měl mít pouze jeden vstup a výstup. S jedním výstupem jsou ale často v praxi problémy, neb je žádoucí někdy podprogram předčasně ukončit, např. proto, že se nepovede načíst vstupní data z databáze. Pro taková ukončení se hodně používají tzv. výjimky. Ve funkci dokmozne i přes použití příkazu goto máme stále jeden výstup z funkce, takže vše je OK.

Pátý krok, funkce vratpuj(pujcka,hotovost):

Jedná se o jednoduchou proceduru. Jakmile zákazník dokončí svoji transakci, tak vrátí bankéři všechny zapůjčené peníze ve všech měnách.

 procedure vratpuj(var pujcka,hotovost:H);
   var 
    mena: D;
   begin {vratpuj}
    for mena := 1 to pocmen do
      hotovost[mena] := hotovost[mena] + pujcka[mena]
   end;  {vratpuj}

Šestý krok, funkce vsetrdok(stav:S):boolean:

Funkce zjistí, zda na konci všech transakcí bankéřův kapital se rovná jeho hotovosti. Pokud ano, vše dobře dopadlo, pokud ne, bohužel přišel o část svého kapitálu. Zkuste se zamyslet nad tím, zda může přijít i o veškerý kapitál. Použití proměnné pomoc typu pole a proměnné c typu integer je myslím jasné.

 function vsetrdok(stav:S):boolean;
  var
   mena : D;
   pomoc: array[D] of boolean;
   c:integer;
 begin
  with stav do
   for mena := 1 to pocmen do
     pomoc[mena] := (kapital[mena]=hotovost[mena]);
   for mena := 1 to pocmen do
     if (pomoc[mena]=false) then c:=1;
   if (c<>1) then vsetrdok:=true else vsetrdok:=false;
 end; 

Sedmý, poslední, krok:

Konečně si napíšeme výslední program. Pro jednoduchost ladění a zadávání vstupů jsem počet měn v programu omezil na jednu jedinou. Pochopitelně vstupy můžete naprogramovat univerzálně, tj. na vstupu se nejdřív zadá počet měn, počet zákazníků a teprve až pak vlastní hodnoty popisující danou situaci.

program banker;

uses crt;
const
 poczakaz = 3;
 pocmen = 1;
type
 B = 1..poczakaz;
 D = 1..pocmen;
 H = array [D] of integer;
 S = record
       transakce: array [B] of
          record
              pozadavek,pujcka: H;
              dokonceno: boolean;
          end;
       kapital,hotovost:H;
     end;

function jisty(beznystav:S): boolean;
var stav: S;

 procedure doktrans(var stav: S);
 var zakaznik: B; pokracuj: boolean;

  function dokmozne(pozadavek,hotovost:H):boolean;
   label 11;
   var
    mena: D;
   begin {dokmozne}
    for mena := 1 to pocmen do
      if (pozadavek[mena] > hotovost[mena]) then
       begin
        dokmozne:=false;
        goto 11;
       end;
        dokmozne:=true;
    11:
   end; {dokmozne}

  procedure vratpuj(var pujcka,hotovost:H);
   var 
    mena: D;
   begin {vratpuj}
    for mena := 1 to pocmen do
      hotovost[mena] := hotovost[mena] + pujcka[mena]
   end;  {vratpuj}

 begin {doktrans}
 with stav do
  repeat
   pokracuj := false;
   for zakaznik := 1 to poczakaz do
    with transakce[zakaznik] do
    if (not dokonceno)  then
    if (dokmozne(pozadavek,hotovost)) then
         begin
          vratpuj(pujcka,hotovost);
          dokonceno := true;
          pokracuj := true;
         end
  until (not pokracuj);
 end; {doktrans}

 function vsetrdok(stav:S):boolean;
  var
   mena : D;
   pomoc: array[D] of boolean;
   c:integer;
 begin
  with stav do
   for mena := 1 to pocmen do
     pomoc[mena] := (kapital[mena]=hotovost[mena]);
   for mena := 1 to pocmen do
     if (pomoc[mena]=false) then c:=1;
   if (c<>1) then vsetrdok:=true else vsetrdok:=false;
 end;

begin {jisty}
 stav:= beznystav;
 doktrans(stav);
 Jisty:=vsetrdok(stav);
end;  {jisty}

var vychstav:S;
    w:char; {vyznam jen pro testovani ukonceni programu}
    cislo:integer; {jen pomoc k nacteni logicke promenne}

begin
clrscr;
{zde je dlouhy nudny blok vstupu programu}

write('Zadej kolik ma pujceno 1 zakaznik: ');
readln(vychstav.transakce[1].pujcka[1]);
write('Zadej jaky je pozadavek 1 zakaznika: ');
readln(vychstav.transakce[1].pozadavek[1]);
write('Zadej 0 nebo 1 ukonceni transakce u 1 zakaznika: ');
readln(cislo);
if cislo=1 then vychstav.transakce[1].dokonceno:=true
           else vychstav.transakce[1].dokonceno:=false;
writeln;

write('Zadej kolik ma pujceno 2 zakaznik: ');
readln(vychstav.transakce[2].pujcka[1]);
write('Zadej jaky je pozadavek 2 zakaznika: ');
readln(vychstav.transakce[2].pozadavek[1]);
write('Zadej 0 nebo 1 ukonceni transakce u 2 zakaznika: ');
readln(cislo);
if cislo=1 then vychstav.transakce[2].dokonceno:=true
           else vychstav.transakce[2].dokonceno:=false;

writeln;

write('Zadej kolik ma pujceno 3 zakaznik: ');
readln(vychstav.transakce[3].pujcka[1]);
write('Zadej jaky je pozadavek 3 zakaznika: ');
readln(vychstav.transakce[3].pozadavek[1]);
write('Zadej 0 nebo 1 ukonceni transakce u 3 zakaznika: ');
readln(cislo);
if cislo=1 then vychstav.transakce[3].dokonceno:=true
           else vychstav.transakce[3].dokonceno:=false;
writeln;

write('Zadej celkovy kapital bankere: ');
readln(vychstav.kapital[1]);

write('Zadej kolik ma banker k dispozici: ');
readln(vychstav.hotovost[1]);
writeln;

{ted zavolame jadro programu, tj. funkci Jisty}

if (Jisty(vychstav)) then writeln('Jedna se o jisty stav')
                     else Writeln ('Jedna se o nejisty stav');

textcolor(red);
writeln('napis k a potvrd  entrem pro ukonceni programu');
repeat
       if keypressed then readln(w);
until w='k';
end.

Ještě jeden důležitý postřeh na závěr našeho povídání o strukturovaném programování. Když se pozorně podíváme na výsledný program, přičemž tolerujeme barbarsky nestrukturovaně napsané vstupy programu, shledáme jej zdánlivě hezky čitelným, koneckonců je krátký, ale vychutnat jeho krásu a eleganci bez pochopení logiky jeho postupného vznikání velikou šanci nemáme, a již nemluvě o pramalé šanci zapracovat do programu např. další funkcionalitu či najít sémantickou chybu. Právě v systematičnosti tvorby vidím kouzlo strukturovaného programování. Holt je to někdy jako např. u jídla, většinou nás zajímá jenom výsledek, ale někdy chceme znát i tajemství přípravy. V neposlední řadě strukturované programování je i o kráse, eleganci a potěšení z tvorby.

A co napsat těsně před závěrem a co na úplný závěr? Před závěrem ještě zdánlivá maličkost, strukturovaný program by měl mít jeden jediný konec programu. Abych základní text příliš nerozšiřoval, k tomuto problému jsem napsal doplněk. Na závěr našeho povídání vám přeji hromadu píle, bez té to totiž nejde, a vůbec hodně zdaru při objevování krásy strukturovaného programování.

Doplněk

Jak již bylo v závěru článku uvedeno, strukturovaný program by měl mít jeden jediný konec programu. Dodržet tohle pravidlo nemusí být vždy jednoduché. Vše si ukážeme na jednoduchém příkladu, který jsem převzal z výborného článku Jiřího Makovičku: Teorie a praxe strukturovaného programování, vyšel v MAA č.8 v roce 1987.

Asi každá z nás by okamžitě nakreslil vývojový diagram podobný tomu na obrázku níže. Bohužel ale je nestrukturovaný, protože diagram má dva konce.

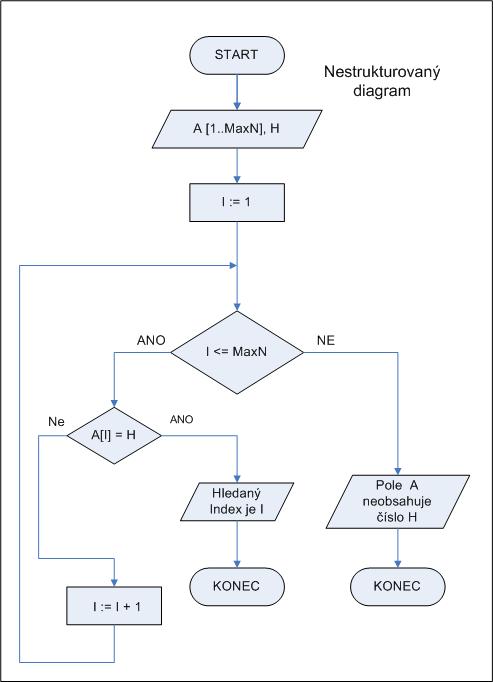
Co s tím? Použijeme klasickou fintu. Zavedeme si pomocmou logickou proměnnou L a pomocí ní problém vyřešíme. Jak na to, nám ukazuje další obrázek. Na počátku cyklu přiřadíme proměnné L hodnotu false. Jakmile narazíme na první hodnotu indexu I, kde platí podmínka A[I]=H, proměnné L přířadíme hodnotu true. Tím si zajistíme, že v hlavním rozhodovacím bloku i v rozhodovacím bloku s podmínkou L=false se vydáme větví NE. Nejtěžší je napsat podmínku (I <= maxN) and (not L). Jinak tahle finta se běžně v programování používá, takže si ji dobře zapamatujte.

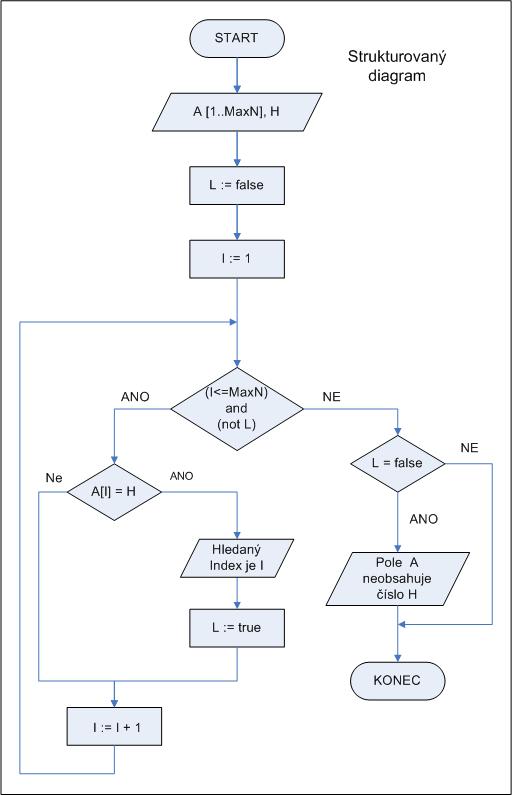
Doporučuji vám diagramy si naprogramovat v libovolném jazyce a sledovat hodnoty proměnných a větve, po nichž program běží, když H bude takové, že se splní resp. nesplní podmínka A[I]=H.

V Brně 11. března 2012.

Dovětek z 26. března 2012. Mladý čtenář mi zaslal dotaz, zda je lepší čistě objektové nebo čistě strukturované programování? Obecně: tyhle dva styly programování nestojí proti sobě jako protipóly. Je možné napsat objektově orientovaný (mix použití objektového přístupu s procedurálním přístupem) či čistě objektový program při použití strukturovaného programování. Jinak platí teorém, že co lze napsat pomocí objektového programování, lze napsat i klasickým neobjektovým přístupem, tj. procedurálním přístupem, a opačně. Ovšem sudím je vždy praxe. Dnes dochází v praxi k tak výraznému propojení technologií, programování a využívání již předpřipravených entit (tříd, objektů, webpart, knihoven apod.), že většina programátorů z praxe si strukturovaným programováním hlavu moc netrápí, dokonce si dovolím tvrdit, že kapánek rozsáhlejší program ani čistě strukturovaně napsat neumí. Nemluvě o tom, že v programech napsaných objektově se snaze odhalují a odstraňují chyby. Jsou ale zase oblasti, kde nenapsat program strukturovaně je spíš veliké riziko, než dobrý nápad, např. u překladačů, u složitých algoritmických úloh, koneckonců náš příklad je toho malým důkazem. Donedávna se věřilo, že platí Böhmova - Jacopiniova věta, která tvrdí, že ke každému vývojovému diagramu existuje strukturovaný diagram, který simuluje původní diagram, což znamená, že převod nestrukturovaného vývojové diagramu na strukturovaný by mělo jít udělat čistě formálním postupem, tedy např. programem. Leč dodejme, že tahle věta byla podrobena silné kritice a bylo dokázáno, že obecně neplatí. Tak či onak u kapánek delšího nestrukturovaného vývojového diagramu, který by ještě šlo převést na strukturovaný, by byl automatem vytvořený strukturovaný diagram na 99 % pěkně nepřehledná divočina.

Domů | Prolog 2001: Vesmírná odysea | Nejen básně v próze | Články