Jak sestavit diferenciální rovnici?
Dušan Polanský
Sestavit diferenciální rovnici není obvykle jednoduché. Když jednoduché to je, tak to dokáže kde kdo. Pokud je to těžké a pokud podobnou rovnici ještě nikdo nesestavil, dokonce máte slušnou šanci, že ji po vás pojmenuji, tak jako po svých objevitelích jsou pojmenované mnohé rovnice, např.: Diracova rovnice, Schrödingerova rovnice, Navier–Stokesovy rovnice, Maxwellovy rovnice, Ilkovičova rovnice.
Pokud chceme sestavit nějakou diferenciální rovnici, musíme vycházet z nějakých známých skutečností, ty mohu být vyjádřeny buď nějakým vzorcem či experimentálně získanými daty nebo vysledovanými závislostmi. Diferenciální rovnice vždy vyjadřuje nějakou dynamiku, obvykle v závislosti od času a výchozích podmínek. Ovšem jsou i diferenciální rovnice, v nichž dynamika je, a ještě jaká!, ale přesto čas v nich explicitně nefiguruje, kupříkladu v rovnicích popisujících moderní teorii kvantové gravitace.
Pokud jde o vlastní řešení diferenciálních rovnic u mnohých jejich řešení jsou známá všeobecně, u některých jenom za určitých speciálních výchozích podmínek, např. Einsteinovy rovnice gravitačního pole (jedná o soubor 10 rovnic) no a některé rovnice řešení stále fest odolávají, to jsou např. již zmíněné Navier–Stokesovy rovnice; dokonce tyto matematici zařadili mezi sedm největších nevyřešených otázek matematiky pro toto staletí s nárokem na milionovou odměnu v dolarech.
V našem jednoduchém textu, si sestavíme tři jednoduché rovnice. První bude úplně jednoduchá, snad ani nebude stát za řeč. Druhá bude o něco málo složitější. Třetí nebude také moc složitá, ale na ní si také ukážeme, že tzv. libovolná konstanta, kterou známe z diferenciálního a integrálního počtu může mít docela zásadní výsledek pro celkový výsledek výpočtu a že za určitých výchozích podmínek vůbec není libovolná. Začneme sestavením první, zcela jednoduché, rovnice.
Počet obyvatel Země v roce 2023 je odhadován na 8 miliard. Roční růst populace předpokládejme dlouhodobě do budoucna 1 %. Kolik nás bude za 50 let? Za kolik let nás bude 20 miliard?

Za pozornost určitě stojí skutečnost, že konstantní výraz eC má zcela konkrétní hodnotu, že není libovolný, je to výchozí početní stav populace. Teď přistoupíme k sestavení druhé rovnice, v té budou vystupovat dokonce dvě závislosti na čase.
Sestavme diferenciální rovnici, která vyjadřuje růst objemu meteorologického balónu na čase při jeho napouštění, když víme, že při určitém poloměru balonu je známá rychlost růstu poloměru balónu. Balón má tvar koule. Pro větší názornost vše doložte praktickým výpočtem při vhodně zvolených výchozích hodnotách.

Dodejme, že podobné příklady se již řeší na základní škole, kupříkladu zadání může znít: Jak se zvětší v procentech plocha čtverce, když délku jeho strany zvětšíme o 20 %?
Třetí příklad bude o něco složitější, přičemž zvýšenou pozornost budeme věnovat stanovení hodnoty integrační konstanty. Než se do příslušných výpočtů dáme malé připomenutí látky z fyziky na základní škole.
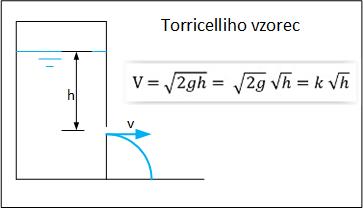
Jedná se o vzorec z hydrodynamiky, který dává do souvislosti rychlost výtoku kapaliny otvorem v nádobě s tekutinou s výškou kapaliny nad tímto otvorem. Tenhle vzorec se lehce odvodí z Bernoulliho rovnice. V reálu je vše o dost složitější, jelikož rychlost ještě závisí i na součiniteli výtoku (zúžení), tvaru otvoru a viskozitě kapaliny. A teď již můžeme přistoupit k zadání.
Z plné nádrže ve tvaru válce o ploše podstavy S vytéká kapalina otvorem kruhového tvaru na dně nádrže o ploše s. Nádrž se zcela vyprázdní za 20 minut, za kolik se vyprázdní nádrž naplněná do poloviny. Zanedbejte součinitel výtoku (zúžení) a viskozitu kapaliny.
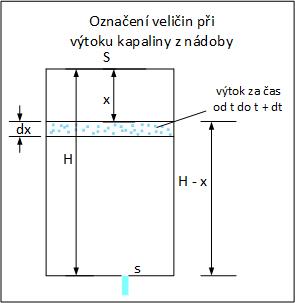
Abychom se dopracovali k řešení, situaci si znázorníme na obrázku. Nejde o nic jiného než si uvědomit, že z nádoby za čas dt vyteče v.dt objemu kapaliny, což je rovno S.dx. Závislost rychlosti v na výšce kapaliny nad otvorem je přitom daná Torricelliho vzorcem.
Po tomto krátkém vysvětlení můžeme přikročit k řešení úlohy. Hodnotu zdánlivě libovolné integrační konstanty stanovíme za základě počátečních podmínek pro x a t.

Co dodat závěrem? Svět diferenciálních rovnic tvoří nejen nejbohatší odvětví matematiky, ale i nejzajimavější. Je to dáno tím, že většina zákonitostí v přírodných vědách, ale občas i v ekonomice, je formulovaná právě ve tvaru diferenciálních rovnic. Takže dost těžko být odborníkem v zmíněných vědách, potažmo v zmíněné ekonomice (tu moc za vědu nepovažuji, když čtu o obrovské zadluženosti téměř všech států světa), pokud nemáme alespoň intuitivní znalosti o tom, jak se diferenciální rovnice sestavují. Snad vám moje povídání k tomu poznání alespoň kousek napomohlo.
Použitá literatura k třetímu příkladu:
[1] Ивашев-Мусатов О. С. Начала математического анализа, Москва, Наука, 1988.
V Brně 3. září 2023.