"Dolování" neznáme ze vzorce
Dušan Polanský
Pokud si ještě vzpomenete na trápení s příklady z fyziky, bylo to vždy stejné. Na počátku bylo zadání, něco je známe a má se spočíst něco, tedy nějaká veličina, obvykle její konkrétní hodnota včetně příslušné měrné jednotky. Postup řešení příkladů byl a je i dnes stejný. Pochopím zadání, ujasním si, který vzorec se k výpočtu hodí, pokud vzorec má takový tvar, že můžu hned dosadit do vzorce zadané hodnoty, tak je dosadím, a spočtu výsledek. Ovšem často se stává, že vzorec je sice správný, ovšem hledanou veličinu musím ze vzorečku odvodit.
Uvedu příklad. Zadání směřuje ke vzorci pro kinetickou energii tělesa o hmotnosti m: K = 1/2 mv2, ale požaduje se spočíst hmotnost m, takže nejprve m musím ze vzorce odvodit, někdy říkám „vydolovat“. A teprve když m vydoluji, mohu dosadit do vzorce známé hodnoty, v našem případě K a v, a spočtu výsledek.
Nevzpomínám si, že by moji učitelé na základní nebo střední škole tomuto „dolování“ věnovali vůbec nějakou pozornost. Na vysoké škole se již předpokládalo, že to znáte.
Nedávno jsem vnučce, chodí na základku, kolem toho něco málo vysvětloval – šlo o vydolování zrychlení a hmotnosti ze vzorce F = m.a –, a tak už když jsem u toho byl, tak jsem se rozhodl dolování neznámé ze vzorce ukázat na několika příkladech. Půjde nám ale jenom o matematický aspekt odvození, tedy nebude nás zajímat, co fyzikálně za vzorcem vězí. Ať je to klidně cokoliv.
Na prvním obrázku jsou vyřešené 4 jednoduché příklady. V zadání je vždy uveden fyzikální vzorec a jsou zadané veličiny, které se mají ze vzorce odvodit. Úkony prováděné při tomto odvození uvádím vpravo za svislicí.
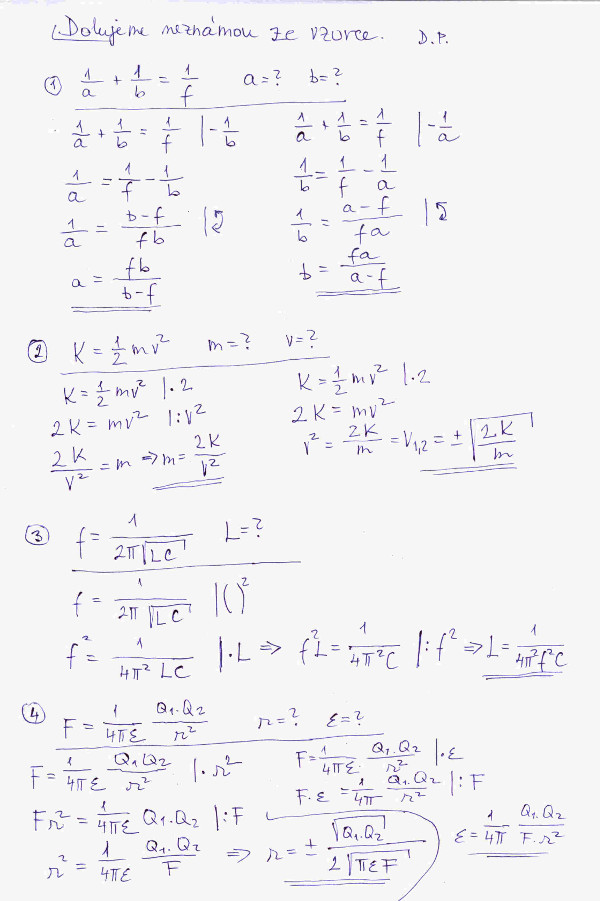
Kdysi jsem náhodou narazil v [1], který je určen pro gymnázia, na zajímavý příklad pro odvození neznáme veličiny z trochu složitějšího vzorce. Neznámá veličina je přímo označena x; viz třetí obrázek. Ovšem při výpočtu kvadratické rovnice se vychází z tzv. „pq“ tvaru, kdy koeficient u mocniny x2 je 1, tedy kvadratická rovnice má tvar x2 + px + q = 0. Na tento tvar lehce můžeme převést každou kvadratickou rovnici tím, že rovnici vydělíme koeficientem u x2. Kupříkladu 5x2 + 10x + 25 = 0, po vydělení celé rovnice 5 dostaneme tvar: x2 + 2x + 5 = 0. Jak se postupuje při odvození řešení z „pq" tvaru kvadratické rovnice je uvedeno na druhém obrázku.

Po této lehce teoretické vsuvce slíbený, o něco složitější, příklad na odvození neznáme x.
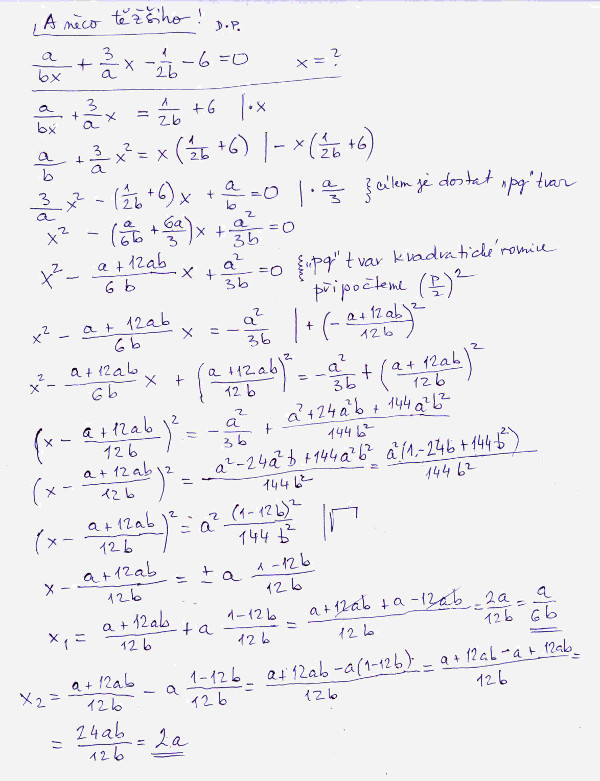
Pokud jste tento příklad zvládli, máte docela vyhráno, ale ne úplně, jelikož neznámá veličina může být „utajena“ i v daleko složitějších vzorcích, kupříkladu může vystupovat jako exponent, tedy mocnitel, nebo jako argument logaritmu apod. Ale to již nechám na vaše učitele.
Použitá literatura:
[1] Burkowitz, Peter: Grundlagen der Arithmetik und der Algebra, CHRIS-LOWDON-STIFTUNG, Hannover, 2003.
V Brně 22. února 2024.