O periodických číslech
Dušan Polanský
Učitelé jsou tu od toho, aby rozdávali radost z poznání a podporovali tvořivost žáků, učňů a studentů (školáci). Neměli by se vytahovat, že toho více než školáci, nebo je strašit tím, že když nebudou znát to nebo ono, že skončí nedobře. Jak všichni víme, mnozí, kteří tomu ve škole moc nedali, to někdy dotáhnou docela daleko. Není to sice častý jev, ale stává se to.
Ale zpět k tomu rozdávání radosti z poznání. Vzpomínám si, jak ještě na základní škole někdo z učitelů napsal na tabuli tuhle rovnost 0,99999... = 1 (tedy 9 je perioda). Myslím si, že tehdy nikdo z nás tomu moc nevěřil, a chtěli jsme, aby nám to vysvětlil. Nevysvětlil, jenom se na nás spokojeně díval, jak jsme z toho pěkně vykuleni.
O hodně později, je tomu asi dvacet let pozpátku, mě požádal jeden soused, který vtloukal do hlavy svému potomkovi matematiku, o rozumné vysvětlení toho, že když se zaokrouhlí 0,083, kde 83 je perioda, je z toho přibližně 0,084. A ukázal mi to v knize, jejímž autorem je Karel Kindl, a která se jmenuje: Matematika, přehled učiva základní devítileté školy. Jelikož knihu v knihovně mám, jedná se o vydání z roku 1975, a ono tvrzení (bez důkazu) je na straně 95 nahoře. Chtěl jsem mu zaokrouhlení vysvětlit řádně, což by ale zabralo nějaký čas, ale na to neměl náladu, tak jsem mu periodické číslo rozepsal: 0,0838383 … a řekl mu, že 0,0838 zaokrouhlíme na 0,084. Byl spokojen.
No a protože chci vám rozdat trochu radosti z poznání z matematiky, tedy pokud o takovou radost stojíte, pokusím se tyhle dvě matematické pravdy, tedy že 0,99999... = 1 a že periodické číslo 0,083, kde 83 je perioda, se opravdu přibližně rovná 0,084.
Tři důkazy toho, že opravdu 0,99999... = 1 můžete vidět na obrázku č. 1. Třetí důkaz chce malé vysvětlení, protože se opírá o větu, která spadá to teorie nekonečných řad, což je látka, která se učí obvykle až na vysokých školách. Ovšem tahle nekonečná řada bude většině středoškoláků asi povědomá, je to totiž geometrická řada. Ta se pozná podle toho, že každý další člen této řady vznikne násobením předchozího členu stejným koeficientem. Zajímavé je, že součet takovéto nekonečné geometrické řady se spočte velice jednoduše za předpokladu, že koeficient je v rozmezí od –1 do +1. Výpočet součtu je ukázán na řadě, jejíž koeficient je 0,5. Přiznám se, že třetí důkaz se mi líbí nejvíce, dává vyniknout kráse matematických výpočtů.
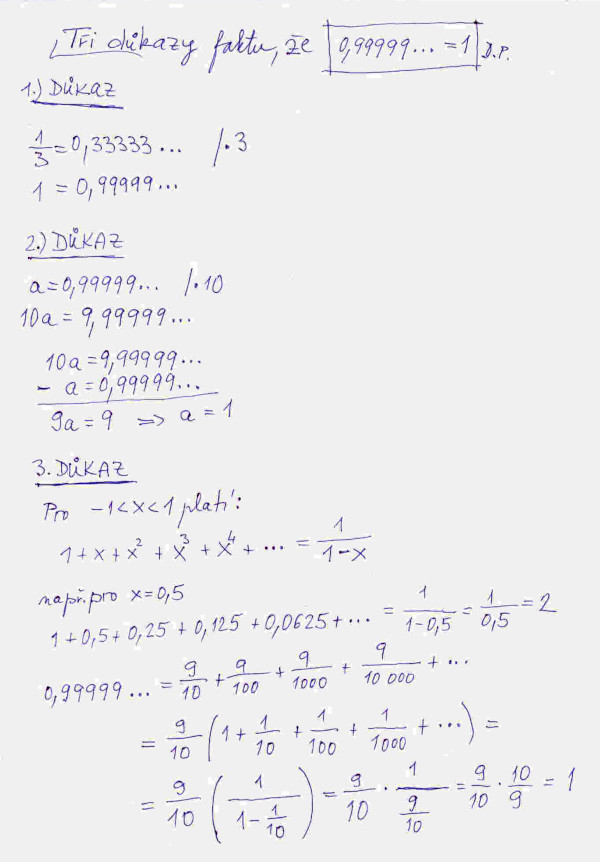
Pokud je o důkaz toho, že když se zaokrouhlí 0,083, kde 83 je perioda, je z toho přibližně 0,084, bude výklad trochu rozvláčnější. Určitě víte, že čísel je více druhů. Jsou to přirozená čísla (1, 2, 3, …); celá čísla (0, ±1, ±2, …); racionální čísla (např. 7/9, 15/17 atd.); iracionální algebraická čísla, jež jsou řešením algebraických rovnic s racionálními koeficienty (např. √4); iracionální transcendentní čísla, jež nejsou řešením žádné algebraické rovnice s racionálními koeficienty (např. e, ln2); reálná čísla, coby součet racionálních a iracionálních čísel (např. √2 , –10, e); algebraické čísla jsou taková, která jsou řešením (tedy kořenem) nějakého mnohočlenu (polynomu) s racionálními koeficienty (např. iracionální číslo √2 je algebraické číslo, protože je řešením rovnice x2 – 2 = 0); transcendentní čísla, viz již výše (např. e, π); komplexní čísla (např. 2 + 6i, kde i je imaginární jednotka). Sice ještě by se něco našlo, např. kvaterniony, které jsou rozšířením komplexních čísel, ale to je už svět abstraktnější algebry, který je mimo záběr zájmu většiny z nás.
Když už jsem zmínil reálná čísla, nedá mi to, abych nezmínil krásnou a málem nepochopitelnou vlastnost reálných čísel: Mezi každými dvěma reálnými čísly leží nekonečně mnoho racionálních i nekonečně mnoho iracionálních čísel. Jenom dodám, že zmíněná reálná čísla mohou být vedle sebe jakkoliv blízko. Uznejte, že je to na palicu.
Proč jsem si dal práci s vyjmenováním tolika druhů čísel? To proto, abychom si uvědomili, že periodická čísla patří do světa racionálních čísel, tedy platí, že každé periodické číslo je racionální číslo. Vše ostatní, co potřebuje člověk k pochopení toho, že když se zaokrouhlí 0,083, kde 83 je perioda, je z toho přibližně 0,084 je uvedeno na obrázku č. 2. Jenom si dovolím upozornit, že stejnou techniku, jakou jsme použili při druhém důkazu rovnosti 0,99999... = 1, jsme využili při převodu desetinných racionálních čísel na zlomky v případě, že perioda začíná hned za desetinnou čárkou. Snad ještě za zmínku stojí fakt, že ne každé desetinné číslo je racionální, kupříkladu Ludolfovo číslo π (přibližně 3,141592653589) nebo Eulerovo číslo e (přibližně 2,7182818284) jsou sice desetinná čísla, ale nejsou racionální, jsou iracionální a dokonce transcendentní. Iracionální číslo má za desetinnou čárkou nekonečně mnoho čísel a není to číslo periodické. Pro zájemce jsem do přílohy dal důkaz toho, že číslo e je iracionální. Ovšem důkazy transcendentnosti Ludolfova nebo Eulerova čísla, tedy, že taková čísla nejsou kořenem žádné algebraické rovnice s racionálními koeficienty, jsou složité.

A jak to vlastně je z naším periodickým číslem 0,9, když na něj aplikujeme postup z obrázku č. 2 pro případ, že perioda začíná hned za desetinnou čárkou. Dobře! Periodické číslo 0,9 můžeme napsat jako zlomek 9/9, což je div se mi světe 1. A máme zde čtvrtý důkaz toho, že 0,99999... = 1. A pak, že matematika nude je!
Je pravda, že dnes se největší pozornosti (i laiků) těší prvočísla, jsou doslova hitem. Vychází o nich hromada publikací. Je to především dáno jejich využitím při šifrování. Snad ale uznáte, že i s periodickými čísly je docela zábava. Pokud se mnou alespoň trochu souhlasíte, tak jsem tenhle text nenapsal zbytečně.
V Brně 21. února 2025.
Příloha: Na obrázku č. 3 je uveden důkaz toho, že Eulerovo číslo e je iracionální.
