Rekurze pro úplné začátečníky
Dušan Polanský
Rekurze mě docela fascinuje, sice ne jako krása žen, ale fascinuje. Asi nejsem jediný, neboť na internetu je hromada článků kolem rekurze. Možná je to proto, že se při programování rekurze poměrně hodně využívá, ale možná i z toho důvodu, že nás přitahuje něčím tajemným. Mé povídání je určeno pro úplné začátečníky. Většina článků o rekurzi je zatížena zápisy procedur v programovacích jazycích, což může laika či začátečníka odradit od čtení. Tomuto se sice zcela nevyhýbám, zde probírané tři školské příklady jsem nakonec zapsal v programovacím jazyce JavaScript, ale jsou to spíš ilustrační doplňky. Koneckonců JavaScript téměř neznám. Mám dva neskromné cíle: začátečníkovi vysvětlit, co to rekurze je, a nastínit mu jak se k definování rekurzívnímu výpočtu samostatně dopracovat. Co k tomu potřebujete znát? Bohatě postačí znalost látky ze základní školy a hlavně mít chuť a elán poznat něco nového.
Výklad začneme notoricky známým rekurzivním výpočtem faktoriálu, ale celou krásu rekurze si ukážeme na těžším příkladu, na Hanojské věži. Začneme trochu obecně, takže se nevyděste textu následujícího odstavce.
Když se rekurzívně provádí určitá množina příkazů, znamená to, že v průběhu tohoto provádění se opět vyvolá naprosto stejná množina příkazů jaká se právě provádí a ty se opět začnou provádět. Je to volání sama sebe. Volání sama sebe může proběhnout několikrát.
Na obrázku vidíme, že naprosto stejné skupiny příkazů se začaly provádět třikrát. Spustil se nějaký výpočet, např. si představte nějaký počítačový program obsahující příkazy, z jakéhosi důvodu se nemohl běh výpočtu dokončit, tak se opět vyvolal stejný výpočet a opět se nepovedlo výpočet dokončit, až konečně na třetí krát se z jakési, zatím záhadné, příčiny výpočet podařilo u posledního výpočtu dokončit. Tím se vytvořily podmínky, aby se dokončil i předchozí výpočet a nakonec i ten první, který řetězec volání sama sebe vyvolal. Červeně jsme označili příkazy, které se mohly dokončit až při zpětném návratu.
Naše obecné povídání si demonstrujeme na konkrétním příkladě, na výpočtu faktoriálu. Faktoriál celého kladného čísla se spočítá tak, že vynásobíme mezi sebou postupně všechny celé čísla od 1 až po číslo, jehož faktoriál hledáme, např. FAKT(3) = 1.2.3 = 6, přitom definičně platí, že FAKT(0) = 1. Případně lze postupovat i takto FAKT(3) = 3.2.1 = 6. Výpočet probíhá v cyklech, v každém cyklu snížíme hodnotu čísla, jehož faktoriál hledáme, o 1, dokud nenarazíme na 1. Vývojový program pro výpočet počítačem by mohl vypadat nějak takhle:
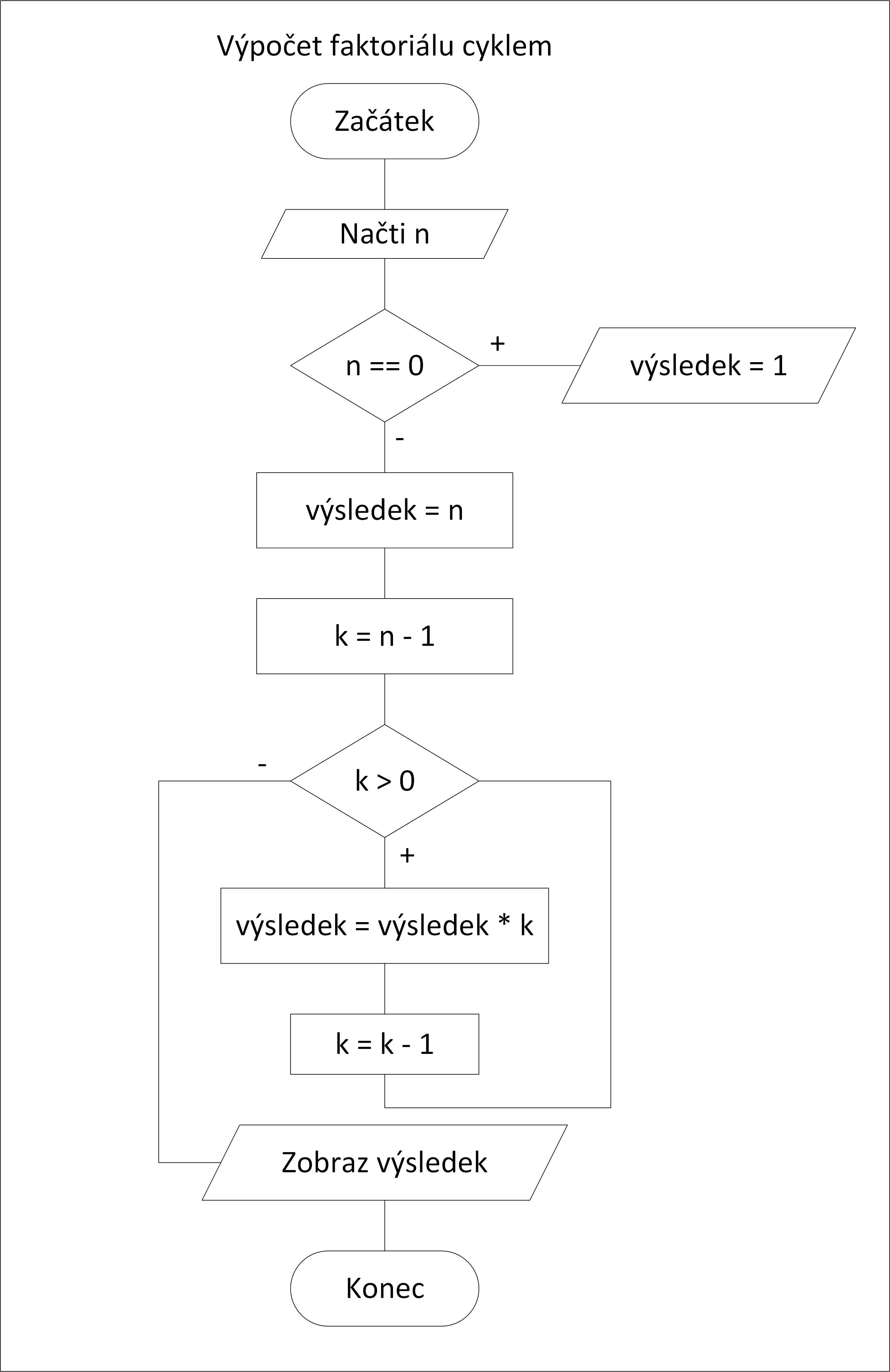
Pro větší názornost jsem napsal krátký program v jazyce JavaScrit (téměř jej neznám) pro výpočet faktoriálu výše uvedenou metodou. Vyzkoušení je jednoduché. Po kliku na odkaz na stránku, je uveden na konci tohoto odstavce, se dostanete na stránku, která neobsahuje nic jiného než program pro výpočet faktoriálu. Zadáte celé číslo, jehož faktoriál chcete spočíst. Po zobrazení výpočtu a kliku na tlačítko OK se můžete podívat na kód prográmku. Stačí kdekoliv na ploše kliknout pravým tlačítkem myši, poté co se rozbalí místní nabídka, zvolíte možnost Zobrazit zdrojový kód stránky. Komentáře by vám měli pomoci se orientovat v kódu. V programu jsou ošetřeny i nesprávně zadané vstupní hodnoty. A tady je slíbený odkaz na stránku s programem.
Leč tohle není rekurzivní výpočet, protože jsme podle definice rekurze při výpočtu ani jednou nevolali výpočet FAKT, např. FAKT(2). Jenom jsme čísla násobili. Pravidlo pro rekurzivní výpočet vypadá zcela jinak: FAKT(N) = N.FAKT(N-1). Na straně pravé voláme stejný výpočet jaký je na straně levé. Dojít na tento vzoreček není vůbec těžké. Ukážeme si to na FAKT(3). Výpočet si napíšeme od konce, tj. FAK(3) = 3.2.1. Vidíme, že vlastní výpočet je vlastně 3.FAK(2), jelikož FAK(2) = 2.1. Když výraz 3.FAK(2) zobecníme na výpočet faktoriálu celého kladného čísla, dostaneme hledaný výraz N.FAKT(N-1). Jak rekurzivní výpočet FAKT(3) probíhá nám osvětlí obrázek.
Výpočet FAKT se nám po volání FAKT(3) vyvolal ještě třikrát. Volání trvalo až do bodu, kde jsme byli schopni výpočet dokončit, a to bylo na posledním řádku obrázku, neboť víme, že definičně FAKT(0) je 1, takže jsem pak mohli vypočíst i FAKT(1) = 1. FAKT(0) = 1.1 = 1. Když už známe FAKT(1), můžeme vypočíst FAKT(2), no a na základě FAKT(2) konečně spočteme FAKT(3). Obrazně řečeno: postupovali jsme směrem dolu, abychom se dostali až ke dnu propasti, tam jsme našli to, co náš sestup zastavilo a umožnilo nám po vystoupání nahoru se dopracovat k tomu, kvůli čemu jsme se do propasti vydali. A tady je odkaz na stránku s programem. Jeho obsluha je naprosto stejná jako v předchozím programu.
Zrekapitulujme si, co jsme k výpočtu faktoriálu celého čísla N potřebovali znát: rekurzivní vzorec FAKT(N) = N.FAKT(N-1) a že definičně FAKT(0) = 1. Tohle schéma se u rekurze objevuje pokaždé. Vše si ukážeme na těžším příkladě. Opět budeme znát jakési pravidlo výpočtu, v němž bude figurovat volání sama sebe a opět budeme znát nějaký elementární fakt. V našem prvním příkladu, tímto faktem bylo, že FAKT(0) = 1. A navíc si u našeho druhého příkladu budeme i hrát, doslova, neboť Hanojskou věž si můžete zakoupit jako hlavolam v hračkářství nebo si hru zahrát na svém PC, viz např. tento odkaz na hanojskou věž. Snad nějakou dobu vydrží.
To, co vidíte na obrázku je trojice Hanojských věží. Označili jsme si je A, B, C. Náš úkol je zdánlivě prostý, máme přemístit kotouče, jsou zakreslené červenou barvou, z věže A na věž C, přitom věž B můžeme využívat jako pomocnou, odkládací. Pochopitelně celé to má nějaký háček, přesněji dva: nikdy nesmí nastat situace, že položíte větší kotouč na menší a vždy se přenáší jenom jeden kotouč. Kotoučů může být teoretický libovolný počet, na našem obrázku jsou 3. Jinak pokud byste měli na věži A 64 kotoučů, tak byste museli provést 18 446 744 073 709 551 615 dílčích kroků, tahů. Pokud by člověk udělal jeden tah každou sekundu a postupoval by nejkratším možným způsobem, tedy optimálně, trvalo by mu to přibližně 600 miliard let. Zvládne to počítač? Je pravda, že superpočítač dokáže provést za sekundu tisíce tahů, ale musím vás přesto zklamat, i tak těch 64 kotoučů nezvládne v rozumném čase. Nemluvě o tom, že velice pravděpodobně zkolabuje, nebuď se mu nebude dostávat paměti na ukládání mezivýsledků. Ale to by již bylo jiné povídání. Raději se vrátíme k hledání řešení pomocí rekurze. Pokud to zvládneme, automaticky najdeme i optimální řešení, to jest neuděláme ani jeden tah navíc.
Takže začneme. Počet kotoučů si označíme N. Nejprve dáme na věž A jeden jediný kotouč, tj. N=1. Řešení je prosté: přeneseme kotouč z věže A na věž C a je vymalováno. Závěr? Důležitý! Naše řešení musí fungovat i pro tento jednoduchý případ, takže určitě se v našem řešení objeví příkaz: Přenes kotouč z věže A na věž C. Současně lze v tomto tahu vytušit i hlubší logiku. Je jasné, že podle zadání největší kotouč musí skončit na dně cílové věže, tj. C, takže určitě nastane situace, že kromě největšího kotouče bude N-1 kotoučů uspořádaných od největšho po nejmenší na jiné věži a my budeme muset přenést největší kotouč ze zbývající věže na cílový kotouč. Této situaci se nelze vyhnout. Nepřipomíná vám přesun z věže A na věž C prostý fakt z prvního příkladu, že FAKT(0)=1? A zkusme v analogii s FAKT pokračovat dál. Jestliže největší kotouč bude na cílové věži, na některé věži nám zůstalo N-1 kotoučů, a pro ty musíme řešit stejný problém jako pro N kotoučů. Nepřipomíná vám to zase vzoreček FAKT(N) = N.FAKT(N-1)?
Teď ale musíme náš problém nějak více uchopit za pačesy. Snad nám pomůže případ s dvěma kotouči, tedy N = 2. Bez dlouhého experimentování zjistíme, že optimální počet tahů jsou 3 tahy. Dáme malý kotouč z A na B, pak veliký z A na C (viz předchozí případ), no a pak přesuneme malý kotouč z B na C. Zkusme náš postup pro dva kotouče zobecnit. Náš problém jsme rozložili na tři dílčí příkazy.
První příkaz. Přenes N-1 kotoučů, což v našem příkladě je jeden kotouč, neboť 2-1 = 1, z věže A na B, přičemž věž C je pomocná. U dvou kotoučů to znamenalo, že jsme malý kotouč dali z věže A na věž B a bylo hotovo. To, že jsme teď pomocnou věž C vůbec nevyužili, je dáno malým počtem kotoučů. U většího počtu věž C jistě využijeme.
Druhý příkaz. Ten již známe z případu s jedním kotoučem! Přenes kotouč z věže A na věž C.
Třetí příkaz. Přenes N-1 kotoučů z věže B na věž C, přičemž A je věž pomocná. Opět jsme to udělali, přenesli jsme malý kotouč z B na C. To že jsme pomocnou věž A opět nevyužili, je dáno malým počtem kotoučů. U většího počtu ji jistě využijeme.
Zkusme si to vše zapsat formálně. Formální zápis ať vypadá takto: Přenes (N, A, C, B). Slovně: Přenes N kotoučů z věže A na věž C, přičemž věž B je pomocná. V našem zápise vždy bude na první pozici počet kotoučů, na druhé věž výchozí, pak cílová a na poslední pozici věž pomocná. A slíbené tři příkazy v našem formalismu:
Zadání: Přenes (N, A, C, B)
Řešení: Přenes (N-1, A, B, C);
Přenes kotouč z A na C;
Přenes (N-1, B, C, A).
A ejhle, naše řešení již rekurzivní je, protože voláme výpočet úplně stejného výpočtu Přenes (počet kotoučů, výchozí věž, cílová věž, pomocná věž) ve vlastním výpočtu dokonce dvakrát. U FAKT to bylo jenom jednou: FAKT(N) = N.FAKT(N-1). Zkusme si naše řešení otestovat na třech kotoučích. Jak bude vypadat strom výpočtu? Docela složitě, proto jsem jej načmáral. Pro větší názornost jsem počet kotoučů dal vždy do kroužku. A fyzicky přenos kotouče jsem vyznačil šípkou ve směru přenosu. Spočtěte kolikrát jsme pro náš případ N=3 rekurzivně volali výpočet Přenes! A zkuste si nakreslit strom volání pro N=4, bude to ale chtít papír formátu A3. Když si strom nakreslíte, správnost vašeho výpočtu si ověřte na opravdové Hanojské věži. Pro N=5 byste již potřebovali veliký arch balícího papíru.
Ještě se nabízí dvě zcela přirozené otázky. První: Kolik dílčích kroků je potřeba vykonat k přemístění kotoučů v závislosti na jejich počtu N? U dvou kotoučů jsem si ukázali, že jsou to 3 dílčí kroky. Když se podíváme na náš poslední obrázek, k přemístění 3 kotoučů jsme potřebovali 7 dílčích kroků, pro N=4 bychom potřebovali 15 dílčích kroků, což poměrně jasně ukazuje na vztah 2N - 1. Lze ukázat, že tento vztah platí zcela obecně. Druhá otázka: Kam dát při prvním tahu z věže A nejmenší kotouč? Na pomocnou, nebo na cílovou věž? Řešení je jednoduché. Začneme jedním kotoučem, což je liché číslo. Kotouč dáme rovnou na cílovou věž. Mějme dva kotouče, což je číslo sudé. Menší dáme na pomocnou věž, větší na cílovou, nakonec malý kotouč dáme na cílovou věž. Odpověď zní: při lichém počtu na cílovou věž, při sudém na pomocnou věž.
Je ještě jeden vzorec ekvivaletní předchozímu pro počet kroků potřebných k přesunu N kotoučů. Je to: 2N-1 + 2N-2 + ... + 21 + 20. Takže pro 64 kotoučů by to bylo: 263 + 262 + ... + 21 + 20. A můžete začít počítat!
Pokud umíte programovat, můžete si uvedený postup přepsat do jakéhokoliv programovacího jazyka. Neměl by to být větší problém. Zkuste zjistit kolik kotoučů vaše PC zvládne přenést. Budete nepříjemně překvapeni. Ne moc! Proč? To by již bylo povídání o tom, jak překladače volání rekurze implementují.
Na ukázku jsem program přepsal opět do JavaScriptu, kód v ostatních jazycích bude velice podobný. Vyzkoušení je opět jednoduché. Po kliku na odkaz na stránku, je uveden na konci tohoto odstavce, se dostanete na stránku, která neobsahuje nic jiného než program pro řešení problému Hanojské věže. Zadáte celé číslo znamenající počet přenášených kotoučů a potvdíte zadání tlačítkem OK. Po vypsání jednotlivých přenosů kotoučů v řádcích pod sebou se můžete podívat na kód programu. Stačí kdekoliv na ploše kliknout pravým tlačítkem myši, poté co se rozbalí místní nabídka, zvolíte možnost Zobrazit zdrojový kód stránky. Komentáře by vám měli pomoci se orientovat v kódu. V programu jsou ošetřeny i nesprávně zadané vstupní hodnoty. A tady je slíbený odkaz na stránku s programem.
A když vám bude i to málo, zkuste si něco přečíst o rekurzivně spočetných množinách nebo formálních jazycích, které jsou rekurzivně spočetné. Dočtete se tam, že formální jazyk je rekurzivně spočetný, když pro něj existuje Turingův stroj. Co to je? No, to je hrozně jednoduchý počítač, který sice umí toho milionkrát méně než vaše PC, ovšem má nekonečnou paměť, což zase váš počítač nemá. Pokud jsem vás alespoň jednoho čtenáře navnadil, tak článek nebyl zbytečně napsán. Pokud nenavnadil, sice škoda mého času, ale přesto se nic neděje, určitě mí čtenáři budou dobří v něčem jiném. A to je důležité! Být dobrý alespoň v něčem, tedy kromě lumpáren.
Základ napsán 8. až 12. srpna 2012. Naposled aktualizováno v Brně 27. 4. 2016.
Doplněk z 29. července 2024. V matematice je hodně vzorců využívajících rekurzi. Nejednou je to tak, že určitý výpočet lze provést rekurzivně i nerekurzivně. Je tomu už nějaká doba, co mi jeden student poslal dotaz, zda znám vzorec na rekurzivní výpočet kombinačních čísel, někdy se jim říká i binomické koeficienty. Náhodou znám. Ale aby z něj něco měli i čtenáři, uvedu jeho důkaz (běžně se neuvádí) a jednoduchý příklad, jak rekurze v tomto případě funguje. Obecně nám půjde o nalezení vztahu, kde kombinační číslo (n nad k) závisí nějakým funkčním vztahem na (n-1 nad k-1). Pokud takový vztah nalezneme, máme vyhráno.
Důkaz bude vycházet z hledání navzájem různých dvojic (a, A), kde a je elementem množiny N mohutnosti n, A je podmnožinou mohutnosti k množiny N. V krajním případě A = N. Tyto dvojice můžeme hledat dvěma způsoby. Při prvním způsobu fixujeme postupně jednotlivé prvky množiny N a určíme všechny prvky množiny A, které obsahují vybraný prvek. Druhý způsob je opačný. Budeme postupně fixovat jednotlivé prvky množiny A, a uvedeme prvky, které obsahují. Protože jsme u kombinací pochopitelně nebude záviset u prvků množiny A na jejich uspořádání. Či budeme postupovat prvním nebo druhým způsobem počet dvojic (a, A) by měl být stejný. Půjde už jeno o to, vyjádřit tyto počty šikovně pomocí kombinačních čísel. Další detaily viz obrázek.
