O substituci t = tg(x/2)
Dušan Polanský
Něco úvodem
V tomto matematickém povídání se chci věnovat trochu těžší látce, které se obvykle na technických vysokých školách v matematice moc pozornosti nevěnuje, a přitom v určitých teoretických výpočtech např. ve fyzice na tuhle látku narazíte. Pokusím se vše podrobně a názorně vysvětlit. Pokud zpočátku se budete ve výkladu ztrácet, zachovejte klid, z příkladů vše pochopíte.
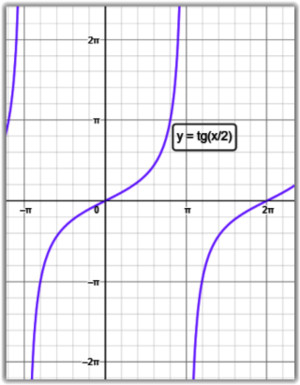
Jde o výpočet integrálů, kde integrovaná funkce má tvar R(sin x, cos x). Písmeno R znamená, že sin x a cos x jsou spolu spojeny jenom racionálními operacemi, tedy nesmí se tam vyskytnout např. výraz kde sin x bude pod odmocninou nebo např. výraz xsin x. Teorie nás učí, že integrály tohoto typu lze vždy převést substitucí t = tg (x/2) na integrály z racionální funkce proměnné t. Bohužel často vychází získaná lomená racionální funkce proměnné t složitá, a pak se člověk docela natrápí z rozkladem racionální lomené funkce na parciální zlomky. Je pravda, že dnes nám v tom může pomoci AI či jiné programy, ovšem i přesto je to jenom polovina problému, druhá spočívá v tom, a bohužel té se často nevěnuje ve vysokoškolských učebnicích při výpočtu určitých integrálů pozornost, že funkce tg(x/2) má bod nespojitosti v bodě π, potažmo jeho násobcích, viz obrázek č. 1; číslo obrázku zjistíte po najetí kurzoru myši na příslušný obrázek. Když se k bodu π blížíte zprava hodnota funkce tg (x/2) se blíží k plusovému nekonečnu, když zleva tak k mínusovému nekonečnu. A teď si představte, že máte spočíst určitý integrál kde integrovaná funkce má tvar R(sin x, cos x) v mezích od 0 do 2π. Tyhle integrační meze jsou docela typické např. pro výpočty v nebeské mechanice, ale i v dalších oblastech teoretické fyziky. Ovšem v intervalu od 0 do 2π zlobí bod π v důsledku transformace t = tg (x/2). Co s tím? Nebudeme nad touto komplikací lamentovat a vše si vysvětlíme na dvou jednoduchých, velice podobných, ale docela poučných příkladech.
Vlastní výpočty
Než se do zmíněných příkladů pustíme, na obrázku č. 2 si uvedeme vše to, co k výpočtu budeme potřebovat z pohledu techniky výpočtů. V bode č. 1 jsou odvozeny vzorečky potřebné pro aplikaci transformace t = tg (x/2) na výpočet integrálů, kde integrovaná funkce má tvar R(sin x, cos x). V bodě č. 2 je odvozen vzorec, který se při integrování často používá. V bodě č. 3 je uveden výpočet neurčitého integrálu pomocí substituce t = tg (x/2); integrovaná funkce má tvar 1/(3 – cos x) a je spojitá na celém intervalu R.
Ještě si připomeňme z náuky o goniometrických funkcích poznatek, že limita funkce arctg(x), když x se blíží k plus nekonečnu je π/2, když x se blíží k mínus nekonečnu je - π/2. Tenhle poznatek budeme hodně v dalším využívat.

Pokud jde o výpočet neurčitého integrálu, k výsledku jsme se dopracovali vcelku snadno, ale je tu problém, který budeme muset později dořešit. V čem vězí? Integrovaná funkce je spojitá na celém oboru R, ovšem primitivní funkce F(x) (tedy výsledek integrování) zlobí v bodě π a jeho násobcích, zde je všude nespojitá, což je názorně vidět na obrázku č. 3.
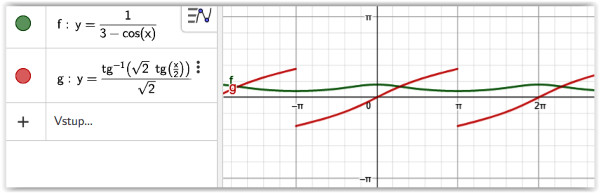
Co s tím? Když se na obrázek podíváme, je jasné, že to chce šikovně dodefinovat F(x) v bodě π a šikovně posunout funkci F(x) tak, aby se stala spojitou. Proč si můžeme tyhle triky dovolit? Důvod je prostý, víme, že každá primitivní funkce obsahuje i konstantu C a derivace jakékoliv konstanty je nula. Takže máme při dodefinování F(x) relativně bohatý manévrovací prostor, ale zase ne absolutní! A také nám to dovoluje definice integrálu podle pánů Isaaca Newtona a Gottfrieda Wilhelma Leibnize. Pokud jde o výpočet určitého integrálu, víme, že to znamená výpočet plochy pod integrovanou funkcí.
Než se k tomuto příkladu vrátíme spočteme si určitý integrál z obrázku č. 4. Integrovaná funkce opět není složitá, je hezky spojitá na celém intervalu R, takže výpočet neurčitého integrálu nám nebude dělat problém. Ovšem ten vyvstane opět v té chvíli, jak budeme mít spočíst určitý integrál v mezích od 0 do 2π. Jak jsme si již výše uvedli, jedná se o docela časté meze integrace např. v teoretické fyzice. Vidíme, že problém je v bodě π. To je důvod, proč si v tomto bodě č. 2 spočteme hodnotu nespojitosti F(x). Teď nám již nic nebrání definovat šikovně zobecněnou primitivní funkci Fo(x) a spočíst požadovaný určitý integrál.

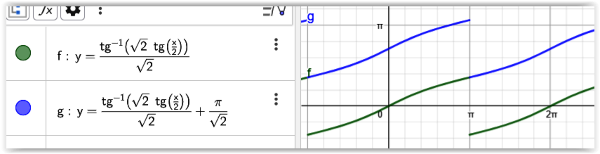
Na obrázku č. 5. vidíme názorně, že touhle šikovnou definicí zobecněné primitivní funkce se nám podařilo dosáhnout toho, že Fo(x) je spojitá na celém intervalu 0 až 2π.
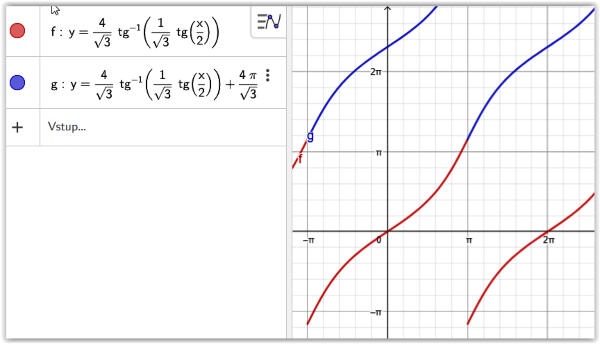
No a teď, když už máme nějakou zkušenost, vrátíme se k dokončení příkladu z obrázku č. 2. Tohle dokončení příkladu již nebudu komentovat. Jistě to hravě zvládněte sami. Jenom si dovolím upozornit, že hodnotu určitého integrálu jsme spočetli dvěma postupy. V postupu A jsme výpočet požadovaného integrálu rozložili na výpočet dvou nevlastních integrálů. Postup B je založen na definování zobecněné primitivní funkce. V příloze je, na osvěžení postupů používaných při derivaci, uveden důkaz toho, že F(x)’ = f(x), viz obrázek č. 8.

A jak jsme se zbavili nespojitosti v bodě π názorně vidíme na obrázku č. 7. Uznejte, že je to málem estetický pohled.
Závěrečné poznámky
Dvě poznámky závěrem. První. Víme, že substituce tg(x/2) při výpočtu integrálu typu R(sin x, cos x) vždy vede k cíli. O tom žádná! Ovšem tahle cesta není vždy jednoduchá, nedejte se zmást tím, že my jsme tuhle substituci použili na dva jednoduché školské příklady. V praxi se snažíme používat i substituce jednodušší. Popis a vysvětlení k některým takovým substitucím lze nalézt ve výborné učebnici [1]. V učebnici je rovněž vysvětlena záludnost použití substituce tg(x/2) při výpočtu neurčitého integrálu, ovšem pokud jsem dobře listoval, chybí tam příklad na výpočet určitého integrálu při použití zmíněné substituce. Přiznám se, že to mě vedlo k tomu, že jsem této látce věnoval zvýšenou pozornost. Pochopitelně v rámci mých možností a znalostí.
Druhá poznámka. V teoretické fyzice se vyskytují daleko složitější příklady integrálů typu R(sin x, cos x). Obvykle se dnes s nimi nikdo moc nemorduje, zjistí si výsledek pomocí např. programu MATLAB. Ovšem vždy je důležité vědět, co za výsledkem vězí, případně si nechat vykreslit vhodným grafickým programem integrovanou funkci a primitivní funkci, tedy výsledek. A pochopitelně pak musí následovat to nejtěžší: interpretace výsledku v kontextu jeho použití. Kde matematikovi práce končí, inženýrovi nebo přírodovědci teprve práci začíná.
Příloha
Důkaz, že F(x)’ = f(x) u prvního příkladu.

Doporučená literatura:
[1] Knichal, Vl., Bašta, A., Pišl, M., Rektorys, K.: Matematika II, SNTL/SVTL, 1966, Praha.
Použitý grafický program:
https://www.geogebra.org.
V Brně ve dnech 15. až 18. července 2025