O absolutní hodnotě
Dušan Polanský
Většina nás se vcelku ráda baví o škole, tedy pokud ji už má z krku. Bavíme se o učitelích, spolužácích, o tom co nás z předmětů bavilo a co ne. Ještě na jaře minulého roku jsem nechtěně vyslechl fragment rozhovoru třech dam v zralém věku, v němž proklínaly vektory a nerovnosti s absolutními čísly. Bylo zřejmé, že dámy dohání maturitu.
Nevím, zda vás na střední škole bavily příklady, v nichž se vyskytují výrazy s absolutní hodnotou, pokud jde o mě, tak by mě určitě nebavily. Použil jsem podmíňovací způsob proto, že já měl to štěstí, že na střední, chodil jsem na stavební průmyslovku, jsme s absolutní hodnotou téměř neválčili. Učil nás starší profesor, jenž hlavně řešil přílišnou malost minisukní holek a u nás přespolních, co jsme dojížděli vlakem, zbytečné obrušování kolejnic, protože prý se pilně neučíme. Budiž mu zem spíš nelehká. Na vysoké škole jsme s absolutní hodnotou pracovali pouze v integrálním počtu, kde se při výpočtech některých integrálů absolutní hodnotě nevyhnete.
Inspirován nadáváním dam na matematiku, jsem si slíbil, že napíšu něco lehkého o absolutní hodnotě. Jenomže chyběla chuť. Až na Štědrý den poté, co jsem splnil úkoly spojené s tímto křesťanským svátkem, nastrojil stromek a vyluxoval, a jelikož dcera neprojevila zájem o hlídání vnoučat a do štědrovečerní večeře zbývaly ještě asi tři hodiny, vzal jsem čistý papír, propisku a začal jsem se bavit s absolutní hodnotou. No a do večeře nečistopis prvních šesti obrázků byl hotov. Sedmý a osmý obrázek jsem napsal o něco později. To by snad na úvod stačilo, dejme se do namáhání hlavy.
Na obrázku č. 1 (číslo obrázku zjistíte po najetí myší na obrázek nebo je uvedeno nahoře červenou barvou v červeném kroužku) je úplně nahoře uvedena nejčastější definice absolutní hodnoty, pod bodem 2 jsou uvedeny vlastnosti nerovností, které budeme při výpočtech používat. Pod bodem 3 je uveden důkaz nerovnosti |x| = |–x|. Při důkazu se vychází pouze z definice absolutní hodnoty, nic víc k němu nepotřebujeme. Jako elementární ukázka praktického využití absolutní hodnoty je v bodě č. 4 uveden výpočet vzdálenosti dvou bodů na ose x.

Na obrázku č. 2 je nakreslený graf velice jednoduché funkce, v jejíž definici se vyskytuje absolutní hodnota výrazu. Pointa nakreslení grafu je v tom, že výraz x – 1 může být podle definice absolutní hodnoty kladný i záporný. Cílem je zjistit, pro kterou oblast na ose x má funkce tvar y = x – 1, a pro kterou y = –(x–1) = 1–x. Bod, kde se funkce láme, nazýváme obvykle kritický bod, někdy i dělící. Je to bod, kde výraz x – 1 má nulovou hodnotu. Ještě jinak, představme si, že x je nepatrně větší než 1, např. 1,1, pak výraz x – 1 je kladný, kdežto pokud bude nepatrně x menší než 1, např. bude 0,9, tak výraz x – 1 je záporný. Vidíme, že vše se točí kolem bodu, kde výraz x – 1 má nulovou hodnotu, tedy kolem bodu 1. Tento poznatek za chvíli využijeme při nakreslení grafu složitější funkce.

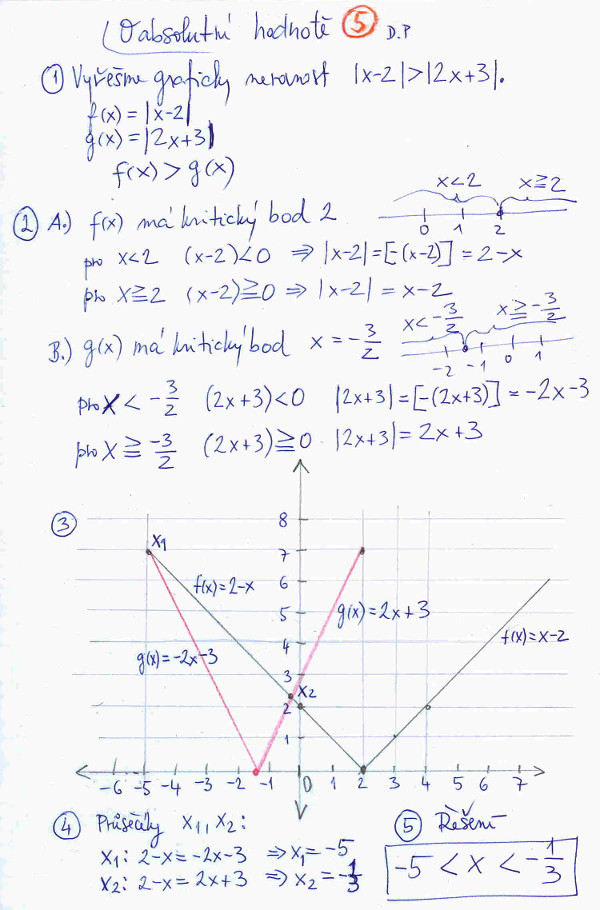
Celá složitost nakreslení grafu na obrázku č. 3 spočívá v tom, že máme dva kritické body, které nám rozdělí osu x na tři obory. V těch musíme chování funkce vyšetřit. Pro každý obor nám vyšla definice vyšetřované funkce jiná. Vlastní nakreslení grafu je již jednoduché.

Na obrázku č. 4 jsou pod body č. 2 a č. 3 uvedeny důkazy některých často používaných nerovností v trochu vyšší matematice.

Na obrázku č. 5 se konečně dostáváme k dámami tolik proklínaným nerovnostem s absolutní hodnotou. Stejnou nerovnost vyřešíme dvěma způsoby. Nejdříve graficky a pak na obrázku č. 6 množinovou metodou. Grafické řešení je přirozenější. Funkci na levé straně označíme f(x), na pravé g(x). Podle zadání příkazu máme zjistit na xové ose obor, kde je funkce f (x) větší než g(x). Grafy těchto funkcí si nakreslíme již výše použitou metodou, a pak zjistíme, kde na xové ose platí: f(x) > g(x). Vidíme, že tahle ostrá nerovnost platí mezi body x1 a x2. Zjistit xové souřadnice těchto bodů není až tak těžké. Stačí vyřešit dvě rovnice o jedné neznámé. Tím dostaneme průsečíky dvou dvojic přímek, které se pokaždé protínají v jednom bodě.
Množinová metoda je méně názorná a je více formalizovaná než metoda grafická. K jejímu řešení musíme znát význam a použití operací množinového součtu a průniku. Postupujeme přitom téměř mechanicky. Protože máme dva výrazy s absolutní hodnotou, mohou nastat čtyři znaménkové kombinace. Jsou uvedené v tabulce na obrázku č. 6. Každou kombinaci znamének vyšetříme zvlášť. Výsledek je dán množinovým součtem těchto čtyř kombinací.

Výpočet na obrázku č.7 se složitostí nepatrně vymyká předchozímu obsahu. Je zde uveden důkaz Cauchy-Schwarzovy nerovnosti. Pokud budete studovat na přírodovědě matematiku nebo fyziku určitě se s ní setkáte v různých podobách a nejen u reálných čísel. Schválně jsem zvolil netriviální důkaz této nerovnosti. Tak to totiž v matematice nejednou chodí. Věhlasný matematik na něco přijde, ale nechce prozradit, jak se k výledku dopracoval, tak použije formální důkaz. Když důkaz nemá, tak vysloví hypotézu, ale jak se k ní dopracoval, stejně neprozradí. V matematice totiž vládne poměrně silný egoismus. Pokud se vám důkaz zdá složitý, můžete si nerovnost jednoduše dokázat tak, že budete uvažovat všecky 4 kombinace reálných čísel p a q, což je vlastně obdoba výpočtu použitého na obrázku č. 6.

V obrázku č. 8 je několik drobností a fint, které si dobře zapamatujte, budou se vám občas hodit. V bodě č. 1 je absolutní hodnota definovaná jako druhá odmocnica z druhé mocniny. Příklad č. 2 demonstruje, jak podle naší původní definice absolutní hodnoty lze někdy velice lehce vyřešit příklad podobný tomu našemu. V bodě č. 3 je dokazaná intuitivně jasná, ale přitom důležitá rovnost. K jejímu důkazu jsme použili definice absolutní hodnoty z bodu č. 1. V příkladu v bodě č. 4 jsme tuto rovnost použili na úpravu výrazu s absolutní hodnotou. V bodě č. 5 je dokazaná jednoduchá, ale v matematické praxi velice často používaná nerovnost. Příklad v bodě č. 6 ukazuje její použití na důležitou nerovnost, s kterou se v matematice potkáváme na každém kroku. Příklad v bodě č. 7 ukazuje, že aplikace nerovnosti z bodu č. 5 vede v určitých případech k velice jednoduchému výpočtu.

Popravdě o absolutní hodnotě toho již víc nevím, takže to je vše.
14. ledna 2016.