Bernoulliho teorém
Dušan Polanský
Vždy jsem byl coby žák na základce nebo student na střední škole nesvůj, když učitel napsal na tabuli bez hlubšího vysvětlení nějaký vzorec a za chvíli se již vesele počítaly příklady - na vysoké to bylo přece jenom jiné, tam čas k hlubšímu pochopení byl v důsledku jiné formy studia. V matematice to ještě šlo, tam většinou nemusíte myslet na to, co vzorec ve vztahu k realitě říká, protože obvykle se od vás chce jenom technické provedení výpočtu, a co vězí za čísly a proměnnými je vám obvykle šum a fuk. Ovšem kupříkladu ve fyzice či v technických vědách je tomu vždy jinak, tam obvykle vzorec popisuje kvalitativně i kvantitativně nějakou hlubokou zákonitost neživé přírody či technické zkušenosti.
Napadlo mě, že bych se coby nematematik mohl pokusit ukázat, dle svých skromných znalostí a inteligenčních možností, že i v matematice je za většinou nevinně vypadajících vzorců schovaný důležitý obsah, který na první pohled nemusí být vůbec zřejmý. Dumal jsem dumal, kam sáhnout, až jsem si vzpomněl na Bernoulliovce a hned jsem si vzpomněl na půvabnou a ne příliš tlustou (142 stran malého formátu) přístupně psanou ruskou knihu autorů B. V. Gnedenka a A. Ja. Chinčina Elementarnoe vvedenie v teoriu verojatnostej; mám 5. vydání z roku 1961. Takže po velice dlouhé době jsem si jakž takž oživil ruštinu a nechal se částečně inspirovat metodikou výkladu zmíněných autorů. Pokud jde o náročnost textu, bohatě vystačíme s matematikou z prvního ročníku na střední škole.
Zpět k Bernoulliovcům. Bylo jich hodně a všem to matematicky a fyzikálně myslelo. Znáte to, když se v rodině daří, tak se daří. No, a když se nedaří, tak to stojí obvykle celé za prd, o tom bych mohl vyprávět málem román v souvislosti s rodinou, v které jsem vyrůstal. To ale nikoho nezajímá, raději si budeme povídat o dílčím matematickém výsledku jednoho z Bernoulliovců, a to Jacoba Bernoulliho (1655 až 1705). Kromě jiného se tenhle švýcarský matematik a fyzik zajímal o teorii pravděpodobnosti, a pokud naši středoškoláci mají v osnovách matematiky úvod do teorie pravděpodobnosti, tak jistě se setkají s tzv. Bernoulliho vzorcem, někdy se mu říká i Bernoulliho schéma. Tento vzorec souvisí s tzv. binomickým rozdělením (buď se něco stane, nebo nestane, žádná další možnost již není) a učí se již jenom proto, že je šikovný na potrápení studentů jednoduchými příklady. Ač nejsem pedagog, vím, že student si má hlavu namáhat, protože když tak nečiní, myslí na ptákoviny a samé příjemné věci, které sumárně ve výsledku vedou k nepříjemným důsledkům pro jeho další život v konzumní společnosti.
O co vůbec v zmíněném vzorci jde? Představme si, že za neměnících se podmínek je pravděpodobnost uskutečnění určitého jevu, např. jevu A, rovná p. Vykonáme n nezávislých pokusů, tedy předpokládáme, že pokusy se nijak neovlivňují (obecně mluvíme o nezávislosti jevů), a zajímá nás pravděpodobnost, že jev A nastane právě k krát. Tedy jev A k krát nastane a n – k nenastane.
Poměrně jednoduchou úvahou lze odvodit vzorec, který tuto úlohu řeší, a jelikož první jej publikoval právě zmíněný Jacob Bernoulli, nese jeho jméno. Výsledný tvar vzorce vidíte na obrázku č. 1 (číslo obrázku zjistíte po najetí myší na něj) pod bodem č. 1. Zatím si další body nevšímejte.
Zdá se vám vzorec složitý? Poud ano, tak malý příklad, na němž logiku vzorce lehce pochopíme. Máme klasickou hrací neciknutou kostku, na které může padnout 1, 2, 3, 4, 5 nebo 6. Vrhneme kostku 3 krát a ptáme se, jaká je pravděpodobnost, že 6 padne dvakrát. Asi malá, ale zkusme spočíst jaká. Označme si padnutí 6 písmenem P a nepadnutí N. Pravděpodobnost padnutí 6 je 1/6, nepadnutí 5/6. Jsou celkem tři možnosti, jak mohou dvě 6 při 3 hodech padnout: PPN, PNP a NPP. Jaká je pravděpodobnost každé trojice? Podle věty o násobení pravděpodobnosti 1/6*5/6*5/6. Výsledná pravděpodobnost podle věty o sčítání pravděpodobnosti bude proto 3*1/6*5/6*5/6 = 0,069. Vidíme, že dle očekávání je opravdu malá. Ovšem k třem možnostem, jak může 6 padnout se lze lehce dopracovat i podle kombinačního vzorce C(n,k) = n!/[k!(n-k)!] = C(3,2) = 3!/[2!(3-2)!] = 3. Takže mechanicky zapsáno: 3*(1/6)2*(1-1/6) = 0,069. No a to je vzorec z obrázku č. 1.

A teď příklad, který bude pro nás motivační i v dalším výkladu. Fabrika něco vyrábí, a to něco splňuje, nebo nesplňuje přesně stanovena kritéria (normy, požadavky). Tedy ve výsledku jsou možné pouze dva výsledky: výrobek splňuje, nebo nesplňuje požadovaná kritéria (tedy máme do dělat s binárním rozdělením). Nech pravděpodobnost vyrobení výrobku, který splňuje požadovaná kritéria, je 0,95. Ze základů teorie pravděpodobnosti víme, že pravděpodobnost, že kritéria nebude splňovat je pak 1 – 0,95 = 0,05. Pokud výrobků v jedné sadě bude kupříkladu 100, dokážeme intuicí vytušit, aniž bychom měli inteligenci Jacoba Bernoulliho, že počet výrobků, které budou požadovaným kritériím vyhovovat, se bude motat kolem střední hodnoty, tedy 95 - lze pochopitelně i matematicky dokázat, že v případě Bernoulliho zobrazení střední hodnota je přesně np. Ovšem v praxi, to asi vždy nebude přesně 95. V jedné sadě takových výrobků bude kupříkladu přesně 95 výrobků splňujících požadovaná kritéria, v druhé 94, ve třetí 97, někdy dokonce všechny výrobky v sadě budou OK. Z výše zmíněného vzorce lze vypočíst pravděpodobnost toho, že výrobků splňujících požadovaná kritéria bude např. přesně 94 nebo i takový extrém, že ani jeden výrobek (tedy všech 100) v celé sadě nebude splňovat stanovena kritéria, což bude jistě velice malá pravděpodobnost, málem nula. Mezi námi, teorie pravděpodobnosti si nepotrpí na zcela jasné a jednoznačné závěry. Je to tak trochu matematická alchymie, podobně jako statistika.
Ovšem je zde praxe a v praxi nás obvykle zajímá otázka formulována jinak, než je dotaz na pravděpodobnost vyrobení přesného počtů výrobků splňujících požadovaná kritéria. V našem příkladu by dotaz mohl znít: Jaká je pravděpodobnost toho, že počet výrobků splňujících požadovaná kritéria bude se pohybovat v intervalu od 93 do 97 výrobků. Což ale znamená, že bychom měli spočíst sumu pravděpodobností P93(100) + P94(100) + … + P97(100) podle již zmíněného vzorce. Takový výpočet může být v případě větších rozpětí (naše je malé) již zdlouhavý. Pochopitelně dnes k podobným výpočtům lze použít i různé programy, jako např. Excel nebo výpočet lze i přímo naprogramovat, tedy pokud člověk programování hoví. Kdysi se hodně používali i předpřipravené tabulky, z nichž lze zmíněné pravděpodobnosti lze jednoduše zjistit. Ovšem, co je metodicky dalece důležitější, je to, že je k dispozici i postup, který podobná zadání umí řešit obecnějším přístupem. A tento přístup se opírá o Bernoulliho teorém, k němuž se ale dostaneme až za chvíli.
Na Bernoulliho vzorec, viz obrázek č. 1, najdete na internetu, pochopitelně i v učebnicích, hromadu příkladů. V případě internetu stačí, když zadáte vyhledat odkazy na výraz Bernoulliho schéma. Ovšem jsem dalek toho, abych vás takovými či podobnými příklady trápil, od toho jsou placeni učitelé, mně spíš půjde o vysvětlení hlubší kvality ukryté v tomto na první pohled dost složitém vzorci. Abychom zmíněnou kvalitu Bernoulliho vzorce vytušili názorně, programem Excel jsem spočetl a zadal vykreslení dvou grafů, vše je vidět na obrázku č. 2 a č. 3.
Na první pohled je vidět, že grafy mají velice podobný průběh. Nejdříve jsou pravděpodobnosti malé, pak stoupají, pak graf dosahuje buď jednoho, nebo dvou hodnot maxima a posléze zase křivka hodnot pravděpodobností klesá. Řekli jsme si, že maximum je u jedné nebo dvou hodnot. Jak poznáme u kolika? Velice jednoduše lze odvodit nerovnost (viz např. zmíněný titul), která platí pro nejpravděpodobnější hodnotu (ko), viz obrázek č. 1, bod č. 2. V bodě č. 3 jsme spočetli nejpravděpodobnější hodnoty pro naše dva příklady na obrázcích č. 2 a č. 3. Vidíte, že výsledky jsou v souladu s grafy.
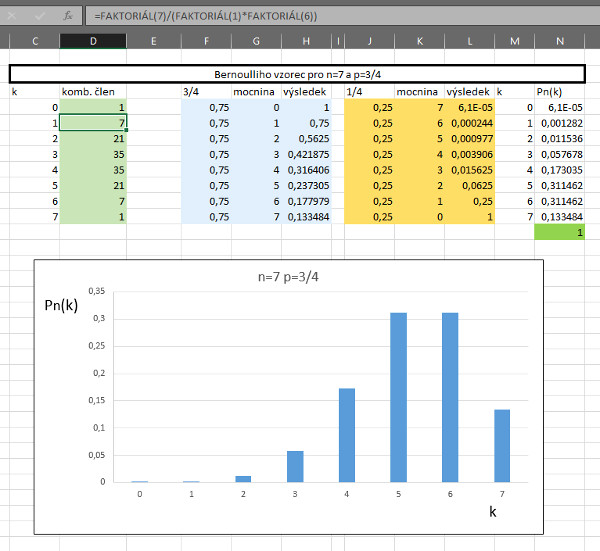
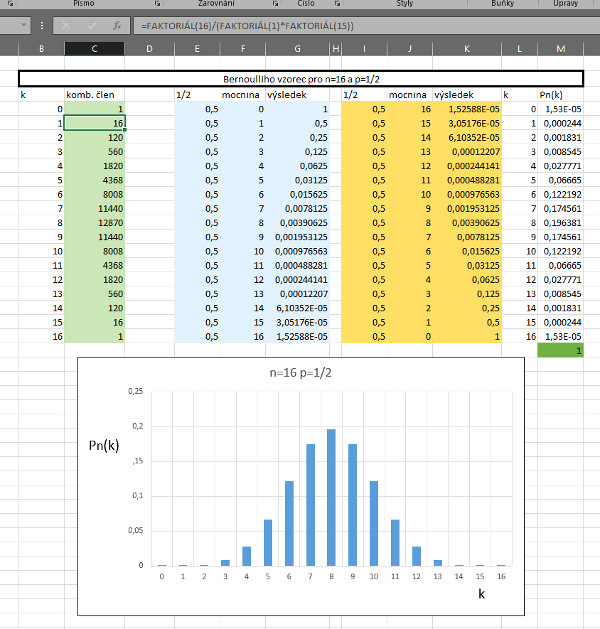
Ale přes tento dílčí počtářský úspěch s nejpravděpodobnější hodnotu (ko) velice opatrně. Podívejme se společně na obrázek č. 3. Vidíme, že pro n = 16 nejpravděpodobnější hodnota počtu nastání sledovaného jevu, jež má pravděpodobnost p = 1/2, je ko=8. Tedy nic, co by nás ohromilo. Stačí si představit, že házím 16 krát mincí. V ideálním případě by 8 krát měla padnout hlava a 8 krát státní znak. Ovšem pravděpodobnost toho, že se tak opravdu v reálu stane, tedy, že 8 krát padne hlava je pouze 0,196!!, což není až tak veliká pravděpodobnost, jak by laik čekal. Proč asi? Důvod jsme již zmínili výše, teorie pravděpodobnosti již ze své podstaty nemiluje otázky na přesný počet nastání jevu, spíš miluje otázky na intervaly. Kupříkladu v našem příkladu s mincí pravděpodobnost toho, že jev nastane 7 nebo 8 nebo 9 krát nám vyjde po sečtení dílčích pravděpodobností (zaokrouhlujeme) 0,174 + 0,196 + 0,174 = 0,544, což je více než 50 procentní pravděpodobnost.
Na obrázku č. 1 v bodě č. 4 jsme zmíněnou nerovnost s ko vydělili n, tedy počtem pokusů a představili si, že číslo pokusů je veliké, pak členy (1–p)/n a p/n budou velice malá čísla, takže si můžeme místo nich myslet nuly, z čehož za tohoto předpokladu dostaneme, že relativní četnost ko/n se při velikém n s poměrně velikou přesností rovná p. Pokud pravděpodobnost vyrobení kvalitního výrobku je 0,95, obratem vytušíme, že z 10 000 vyrobených výrobků jich bude kvalitních přibližně 9 500. Slovíčko přibližně je ale v teorii pravděpodobnosti dost ošidné. Spíš bychom uvítali výsledek v smysluplnější formulaci pro určité rozpětí intervalu, kupříkladu že pravděpodobnost toho, že počet vyhovujících výrobků bude ležet v intervalu 9400 až 9600 je taková a maková.
A intervalovou pravděpodobnost lze spočíst právě pomocí Bernoulliho teorému. Z něj dokážeme vypočítat v jakém intervalu a s jakou pravděpodobností se bude pohybovat počet výrobků s požadovanými kritérii, přičemž je známa pravděpodobnost vyrobení výrobku s požadovanými kritérii.
Kvantitativní vyjádření Bernoulliho teorému v podobě poměrně složité nerovnosti, tedy složité alespoň na první pohled, vidíme na obrázku č. 4 nahoře. Písmeno P znamená pravděpodobnost uskutečnění nerovnosti v kulaté závorce. Vzorce A a B jsou ekvivalentní, obvykle se uvádí jenom tvar A. Když spočítáme hodnotu podle A, výsledek podle B dostaneme odečtením vypočítané hodnoty podle vzorce A od 1. Zkusme si teď nahlas říct vzorec A. Pravděpodobnost toho, že rozdíl v počtu jevů, které v skutečnosti při realizaci nastanou (k) a nejpravděpodobnější hodnoty nastání jevů ko= np je větší než součin epsilon.n, je menší než hodnota p(1-p)/epsilon2n, přičemž epsilon můžeme volit libovolně malé. Číslo n udává v našem příkladu počet vyrobených výrobků, obecně to je počet realizací nezávislých jevů.

Vše nejlépe pochopíme na vyřešeném příkladu, viz obrázek č. 4. Při výpočtu použijeme kvůli pohodlí teorém ve tvaru B. O co vůbec v příkladu jde? Známe pravděpodobnost vyrobení kvalitního výrobku (0,8) a víme, že počet vyrobených výrobků je 200 000. Z toho lehce spočteme nejpravděpodobnější hodnotu ko = n*p = 160 000. Epsilon zvolíme 0,01, je přitom jenom na nás jakou hodnotu zvolíme. Součin epsilon*n nám dá 2000. Výpočet p(1–p) nám dává 0,16, ale moc nepokazíme, když budeme počítat s hodnotou o něco větší, tedy s 0,2, naopak tím se trochu jistíme. Ptáme se, jaká bude pravděpodobnost toho, že počet kvalitních výrobků se bude pohybovat v intervalu 158 000 až 162 000. Odkud se vzal tento interval? Vypočetli jsme jej z nerovnosti |k – 160 000| < 2000. Pro pohodlí čtenáře jsem výpočet nerovnosti zde uvedl, ale v literatuře se obvykle pro jeho triviálnost neuvádí, jelikož interval lze stanovit velice jednoduše: odečteme a přičteme číslo na pravé straně nerovnosti od menšitele na levé straně a máme požadovaný interval. Výsledek našeho výpočtu při zvolené hodnotě epsilon = 0,01 je vidět na obrázku č. 4.
Zkusme si teď místo hodnoty 0,01 za epsilon zvolit 0,001. K výpočtu hledané pravděpodobnosti opět použijeme vzorec ve tvaru B. Výsledek nám vyjde zcela neuvěřitelný! Pravděpodobnost toho, že počet kvalitních výrobků bude ležet v intervalu 159 800 až 160 200, tedy v intervalu velikosti 400 – v předešlém výpočtu byl interval 4 000, tedy 10 krát větší – je přibližně nula, přibližně kvůli zaokrouhlení 0,16 na 0,2. Na první pohled je to překvapující, čekali bychom intuitivně nějakou rozumnější hodnotu, řekněme alespoň 0,07, tedy alespoň 7 % ze 100 %. Kde je chyba? Nikde. Pravdu má naše intuice, ale i vzorec. Jde o to, že vzorce A i B jsou přibližné vzorce, které lze odvodit velice jednoduchými matematickými prostředky, viz např. zmíněnou knihu. Použitím sofistikovanějších matematických prostředků (viz monografie teorie pravděpodobnosti) bychom dostali přesnější odhad, než udávají vzorce A a B. Lze dokázat, že naše vzorce A i B dávají velice slušné odhady, pokud je p blízké hodnotě 1, nebo naopak hodnotě 0.
Na posledním obrázku (č. 5) jsou vyřešeny dva příklady, jež mají názorně dokumentovat, jak se s Bernoulliho teorémem pracuje při konkrétních výpočtech. Příklad č. 2 současně dokumentuje vlastnost zmíněnou o kousek výše, tedy, že vzorce A i B dávají poměrně přesné odhady, pokud je p blízké 1 nebo 0, zde p = 0,95 je blízké 1. Třebaže epsilon = 0,005 je poměrně malé, výpočet ukazuje, že pravděpodobnost toho, že počet kvalitních výrobků se bude pohybovat v intervalu od 189 000 do 191 000 (rozpětí intervalu je 2000) je velice vysoká, málem 100 %. Ovšem tento realtivně slušný odhad se nám podařil jenom díky tomu, že p bylo blízké 1.

A to je vlastně vše. Pokud vás text alespoň trochu zaujal a pochopili jste, že v matematice není ničím neobvyklým, že za zdánlivě nenápadným vzorcem vězí celá hluboká teorie a že intuici uživíme nejen v běžném životě, ale i při matematických úvahách, tak účel textu byl splněn.
V Brně 9. května 2018.