Binomické rozdělení pravděpodobnosti
Dušan Polanský
Znáte to ze školy, učitelé s oblibou žákům nebo studentům opakují: „Tohle máte již dávno znát, nebudu vám to stokrát opakovat!“ Mají i nemají pravdu. Pravdu mají v tom, že je časově nereálné se k již jednou probrané látce opakovaně vracet. Pravdu nemají v tom, že hezký ucelený výklad určité partie i se zopakováním toho, co bude potřeba k pochopení nové látky, učí žáky nebo studenty poznat krásu a propojení poznatků určitého oboru. Bohužel takových ucelených výkladů jsem se ani na základní škole, ani na střední, ani na vysoké nedočkal, protože vždy se pádilo kamsi vpřed. Kam, to jsme nevěděli ani my, ani učitelé. Dnes, když mi je již 64 let si myslím, že je to stejné. Můj názor je, že školy by měly především pěstovat u žáků či studentů celkovou vzdělanost, ne přílišnou specializaci. Vzdělaností ovšem nerozumím povrchní znalost všeho možného, ale hlubokou znalost základů, na kterých bude možno v budoucnu doopravdy něco pevného postavit. Specializace je už věcí praxe, beztak většina učitelů k praxi nikdy nečichla, takže alespoň žáky či studenty neuvedou v omyl bájením o tom, jak to v praxi funguje.
Proč o tom vůbec píšu? Nedávno jsem napsal malé, ale relativně ucelené laické povídání o Bellmanově principu optimality (BPO). Bylo napsáno s minimálním formalismem a od čtenáře kromě určité trpělivosti nic nechtělo, tedy kromě znalosti látky ze základní školy. Na upřesnění dodávám, že BPO se přednáší na vysokých školách technického typu a přírodovědeckých univerzitách. Jeden student mi napsal: „Dokud jsem si nepřečetl váš článek, vůbec jsem nechápal, o co jde, protože učitel nám to vyložil velice složitě, používal složitý formalismus... Váš článek jsem doporučil k přečtení kolegům z našeho kroužku.“ Tím vůbec neříkám, že jsem mistr světa, naopak jsem vyložený amatér, pouze konstatuji, že ucelený výklad určité látky bez zbytečného formalismu je nezbytný pro pochopení podstaty problému. Pochvala od studenta mě nakonec nakopla k tomu, že jsem si vzpomněl, že jsem kdysi starší dceři slíbil napsat laické povídání o tom, že i teorie pravděpodobnosti na základní úrovni poznatků není až taková hrůza, jak si myslí nejen ona, ale i mnoho lidí hlavně s humanitním vzděláním.
Na jednoduchém školním příkladu si navíc ukážeme, že i v teorii pravděpodobnosti k stejnému výsledku vedou různé cesty. Budeme si povídat o binomickém rozdělení. Co vůbec pod rozdělením náhodné proměnné v teorii pravděpodobnosti rozumíme? Rozdělení nám vzorcem nebo grafem či tabulkou říká, jakou četnost (tedy počet výskytů) mají jednotlivé hodnoty vyšetřované náhodné proměnné. Klasickým, často uváděným, příkladem náhodné proměnné je výška dospělých mužů. Jak bychom postupovali, kdybychom chtěli vysledovat nějakou zákonitost u četností podle konkrétních výšek, tedy pokud vůbec nějaká zákonitost pro tuto náhodnou proměnnou platí? Nejprve bychom změřili výšky (výška je náhodná proměnná) všech dospělých mužů např. v Brně (což je už pořádně veliký vzorek). Pak bychom na vodorovnou osu nanesli všechny výšky v mm, které jsme naměřily a na svislou osu bychom nanášeli četnosti (počty výskytů) mužů s příslušnou výškou. Nakonec bychom propojili koncové body vynesených četností. Velice pravděpodobně bychom obdrželi křivku podobnou zvonu. Asi bychom zjistili, že naše křivka má jednu velice příjemnou vlastnost, je symetrická podle nejčastější hodnoty náhodné proměnné. Takže vrchní zaoblení zvonu by bylo u výšek, které se vyskytují nejčastěji. U těch méně častých bychom se pohybovali po stranách zvonu, no a u těch extrémně neobvyklých výšek (či už malých nebo velikých) až kdesi u osy x. Takovému rozdělení říkáme Gaussovo rozdělení. Je často pozorováno při měření náhodné proměnné, jejíž velikost je ovlivněna součtem mnoha malých vlivů (u výšky by tomu tak mohlo být). Pochopitelně náš empirický naměřený zvon asi nebude dokonalý zvon, ale od toho již jsou matematici, aby takový ideální zvon definovali vzorcem, v našem případě tak učinil Carl Friedrich Gauss (1777–1855). Teoretických rozdělení je více než požehnaně a každé z nich definováno jiným vzorcem, a tím i jinou křivkou. Proč tolik rozdělení? Protože náhodných veličin je v našem životě a světě docela hodně a ne pro všechny náhodné proměnné se hodí stejné rozdělení. Uveďme si několik příkladů náhodných proměnných: počty vozidel, které kolem nás projedou za stejných podmínek (vypustíme z měření dny uzávěrek či jiných dopravních omezení) v stejnou dobu (např. od 10,00 hod do 10,15 hod) na stejném stanovišti za určité dostatečně dlouhé časové období, aby bylo možné vysledovat určitou zákonitost, např. za 1 rok; počty diváků na zápasech konkrétního fotbalového klubu v domácím prostředí opět za dostatečně dlouhou dobu, např. celou sezónu; průměrné množství srážek v určité zeměpisné oblasti v určitém období, např. v měsíci listopadu, opět za dostatečně dlouhé období, např. za 100 let. Ovšem vždy je důležité dodržet měření hodnot náhodné proměnné za nezměněných podmínek, na tuhle okolnost se totiž s oblibou zapomíná.
Než si začneme povídat o slíbeném binomickém rozdělení, musíme si říct, jaké znalosti budeme potřebovat, abychom výklad úspěšně zvládli. Požadavků na znalosti sice nebude mnoho, ale pro ty, co jsou již ze střední školy déle ven, tu určitý problém může nastat. Budeme potřebovat zcela elementární znalosti z kombinatoriky a tzv. binomickou větu, kterou sice nebudeme prakticky používat, ale pro pochopení toho, proč mluvíme o binomickém rozdělení, se docela hodí. Ale nebojte se, nenechám vás v tom lítat. Na obrázku č. 1 (číslo obrázku zjistíte po najetí myši naň) je přehled základních pojmů a vzorců z kombinatoriky. Dokonce je toho zde uvedeno více, než budeme potřebovat. V naší úloze vystačíme s pochopením výpočtu faktoriálu a kombinačních čísel. Permutace a variace jsou zde uvedeny jenom pro úplnost. Binomickou větu si zopakujeme, až ji budeme potřebovat. Takže v klidu si zopakujte základní pojmy a výpočty z kombinatoriky podle obrázků č. 1. Jednoduché příklady by vám v tom měly být nápomocny. Co budeme potřebovat z teorie pravděpodobnosti, si na příslušném místě vysvětlíme. Pokud byste chtěli vědět více, můžete si např. přečíst moje elementární povídání O pravděpodobnosti.

Naše úloha: Máme neprůhlednou nádobu, do níž vložíme tři míčky. Každý míček má jinou barvu, jeden je oranžový (o), druhý bílý (b) a třetí modrý (m). Vše ať je zařízeno tak, že dovnitř nádoby nevidíme. Budeme táhnout třikrát, po každém tahu vytažený míček vrátíme zpět do nádoby a pořádně nádobou zahrkáme, aby se míčky dobře promíchaly. Naše zadání zní: Jaké jsou pravděpodobnosti toho, že třemi tahy nevytáhneme oranžový míček ani jednou, že jej vytáhneme jednou, dvakrát a třikrát?
Úlohu vyřešíme třemi postupy: pravděpodobnostním stromem, s použitím věty o násobení pravděpodobnosti a nakonec slíbeným vzorcem pro binomické rozdělení. Pokaždé by nám měl vyjít stejný výsledek.
Řešení pravděpodobnostním stromem. Co to vůbec pravděpodobnostní strom je? Nic složitého. Představte si, že jste mladí manželé a chtěli byste jednou mít dvě děti, a to obě holky. Jaká je pravděpodobnost, že se vám vaše přání splní. Předpokládejme, že pravděpodobnosti narození kluka (K) a holky (H) jsou stejné, tedy 0,5 neboli v procentech 50 %. Při prvním dítěti jsou dvě možnosti, buď se narodí H nebo K. Při druhém dítěti, pokud se jako první dítě narodila H, jsou opět dvě možnosti: narodí se H, nebo K. Pokud se narodil jako první K, jsou u druhého dítěte opět dvě možnosti: H, nebo K. Strom možností vidíte na obr. č. 2.
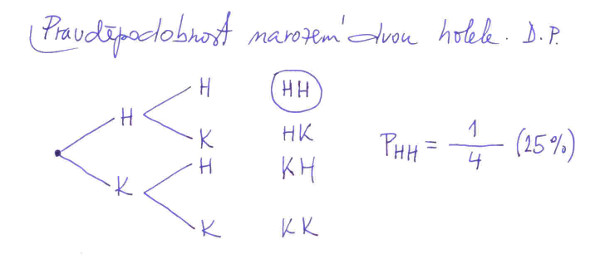
Jaká je námi hledaná pravděpodobnost? Abychom ji spočetli, musíme si říct, jak je definovaná pravděpodobnost. Pravděpodobnost je dána zlomkem: podílem počtu jevu příznivých výsledků k počtu všech možných výsledků. Možným výsledkům se v teorii pravděpodobnosti říká i jevy. V našem příkladu narození dvou holek odpovídá v našem stromě pouze jeden jev, a to HH, přičemž počet všech možných jevů je 4. Z definice pravděpodobnosti nám vychází hledaná pravděpodobnost 1/4, což v procentech je 25 %. Není to moc, ale zase ani málo.
Podobný strom si nakreslíme i pro naši úlohu s míčky v neprůhledné nádobě. Strom i s příslušnými výpočty vidíte na obrázku č. 3. Spočetli jsme všechny možné pravděpodobnosti pro oranžový míček, tj. že nevytáhneme ani jeden oranžový míček, že vytáhneme jeden, dva a tři. Kupříkladu jak jsme spočetli pravděpodobnost, že jsme nevytáhli ani jeden oranžový míček? Prohledali jsme sloupec se všemi možnými jevy, v teorii pravděpodobnosti se všem možnostem, které mohou nastat, říká jevové pole, a spočetli jsme kolik je těch jevů, kde se nevyskytuje písmeno o. To jsou jevy příznivé našemu zadání, tedy abychom nevytáhli ani jeden oranžový míček. Vidíme, že těchto jevů je 8. Všech možných jevů je 27, takže hledaná pravděpodobnost je 8/27. Podobně bychom spočetli další pravděpodobnosti. Kontrola správnosti výpočtu je nabíledni. Pokud budeme táhnout dle zadání našeho příkladu třikrát, určitě nastane jedna ze všech možností, tj. buď nevytáhneme ani jeden oranžový míček, nebo vytáhneme jeden, anebo dva, či tři míčky. To víme jisto jistě, takže pravděpodobnost součtu těchto jevů musí dávat číslo 1, což je pravděpodobnost jistého jevu. Vidíme, že opravdu součet vypočtených pravděpodobností dává číslo 1, tedy jistotu.
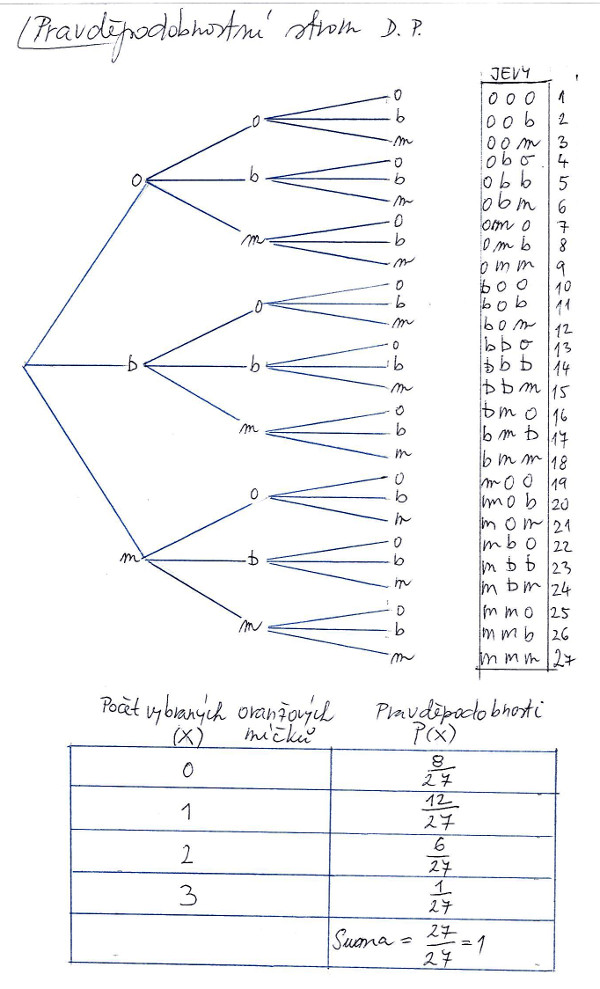
Jak to dopadne, když budeme chtít vědět, jaká je pravděpodobnost, že ve třech tazích s vracením vytaženého míčku vytáhneme 1 nebo 2 oranžové míčky? Věta o sčítání pravděpodobnosti nám říká, že pravděpodobnost vzájemně se vylučujících jevů se rovna součtu pravděpodobnosti těchto jevů. V našem příkladu by to bylo 12/27 + 6/27 = 18/27 = 6/9. Vylučující jevy jsou takové jevy, které nemohou nastat současně. V naší úloze ve třech tazích nemůžeme současně vytáhnout i žádný míček, i 1 nebo 2 nebo 3 oranžové míčky. Může nastat pouze jedna ze zmíněných možností.
Jak to dopadne, když budeme mít dva pokusy po třech tazích s vracením vytaženého míčku a bude nás zajímat pravděpodobnost, že při prvním pokusu vytáhneme 1 oranžový míček a při druhém pokusu opět 1 oranžový míček? K řešení použijeme větu o násobení pravděpodobnosti. Ta nám říká, že pravděpodobnost toho, že určité jevy nastanou současně (v našem případě za sebou) je rovna součinu těchto jevů. Podmínka je, aby tyto jevy byly navzájem nezávislé, tedy aby se nijak neovlivňovaly, což v našem příkladu je splněno, jelikož po každém tažení míček vrátíme do nádoby a nádobou ještě pořádně zahrkáme, takže výsledek druhého pokusu není ovlivněn výledkem prvního pokusu. Jak by to dopadlo v naší úloze. Pravděpodobnost vytažení 1 oranžového míčku ve třech tazích s vracením vytaženého míčku je 12/27, takže pravděpodobnost toho, že se nám povede zopakovat tento výsledek dvakrát za sebou (táhneme třikrát a ještě jednou třikrát) bude: 12/27.12/27 = 16/81.
Uvedením klasické definice pravděpodobnosti a věty o násobení pravděpodobnosti jsme si připravili teoretický základ pro vyřešení naší úlohy metodami klasické teorie pravděpodobnosti. Úspěšný pokus s vytažením oranžového míčku si označíme T (true), neúspěšný F (false). Pravděpodobnost vytažení oranžového míčku je p=1/3. Pravděpodobnost nevytažení je q=2/3. Všimněme si, že p + q = 1. Je to přirozené, když táhnu míček, tak jistojistě buď oranžový míček vytáhnu, nebo nevytáhnu. Vyřešme si spolu případ, že se nám nepodaří ani jednou vytáhnout oranžový míček při třech tazích. Jev, který nastane, si můžeme popsat formálně jako FFF, kde F vyjadřuje výsledek jednoho tažení míčku. Podle věty o násobení pravděpodobnosti pravděpodobnost tohoto jevu bude dána součinem: q.q.q=q3=2/3.2/3.2/3 = 8/27. Zbývající výpočty vidíte na obrázku č. 4. Je vidět, že výsledky jsou stejné, jako při řešení pravděpodobnostním stromem.

Zbývá nám vyřešení úlohy posledním přístupem, tedy pomocí vzorce pro binomické rozdělení. Když se pozorně podíváme na poslední obrázek, vidíme, že při výpočtu požadované pravděpodobnosti jsme pracovali se všemi možnými součiny p a q, za podmínky, že součet mocnitelů byl pokaždé 3, což je počet tažení z nádoby s míčky. Nějak tomu tak je i v binomické větě (viz obrázek č. 5 bod 1), kde členy binomu (binom je dvojčlen) jsme označili dle matematického zvyku a a b. Kdybychom si vzorec pro binomickou větu přepsali s označením členů binomu p a q, hned by nám byla zřejmá silná podobnost s výpočty v předchozím obrázku. Vzorec pro binomické rozdělení je uveden pod bodem č. 2. X je označení náhodné proměnné, tedy počtu vytažení oranžového míčku ve třech tazích. Kupříkladu P(X=0) čteme: pravděpodobnost, že oranžový míček nebude vytažen ani jednou. Kombinační členy v tomto vzorci nám říkají, kolik možných jevů je pro příslušné zadání. Pokud nevytáhneme ani jednou oranžový míček, tak jev FFF se může vyskytnout jenom jednou, proto ve vzorci pro výpočet P(X=0) kombinační člen po jeho výpočtu nám dá 1. Pokud vytáhneme jeden oranžový míček, musí se to stát jednou z 3 možností: TFF, FTF, FFT. Proto ve vzorci pro výpočet P(X=1) kombinační člen po jeho výpočtu nám dá 3. Ve vzorci pro binomické rozdělení musí platit rovnost p + q = 1, což má, jak jsme si již řekli, svoji logiku, buď vytáhnu, nebo nevytáhnu oranžový míček. Třetí možnost již není. Vyřešení naší úlohy vidíme na konci obrázku č. 5. Výsledky jsou stejné, jako u dvou předchozích přístupů. Je vidět, že opravdu k cíli vedou různé cesty.

Vzorec pro binomické rozdělení se nám může zdát v porovnání se vzorci pro většinu jiných rozdělení (viz jakoukoliv podrobnější knihu o teorii pravděpodobnosti) docela jednoduchý a svým způsobem málo použitelný, tedy kromě podobných umělých školních úloh, jako byla ta naše. Je i není to pravda. Pokud byste se zahloubali do teorie pravděpodobnosti více, dozvěděli byste se, že binomické rozdělení lze aproximovat při velkém počtu nezávislých pokusů - již v úvodu zmíněným - Gaussovým rozdělením. Tenhle nejen teoretický, ale i praktický výsledek je obsahem tzv. Moivreovy-Laplaceovy věty. V literatuře lze nalézt i aproximaci binomického rozdělení Poissonovým rozdělením, které patří k docela důležitým a zajímavým pravděpodobnostním rozdělením. A to je zatím vše.
V Brně 26. dubna 2017.