Tak trochu o duchu matematiky
Dušan Polanský
Je správné, když se popularizují různé oblasti vědy, techniky a technologického vývoje. Taková popularizace by měla hlavně sloužit k tomu, aby mladé lidi inspirovali k dalšímu, hlubšímu zájmu o tu kterou oblast vědy či techniky nebo technologií. Problém je nerovnoměrnost tohoto typu literatury podle zmíněných oblastí. Daleko nejvíce populární literatury vychází z matematiky. Pak už je to horší s chemii, ještě horší s technickými vědami a málem úplný deficit převládá v popularizaci vývoje technologií. Pokud jde o fyziku zdání klame, sice hromady populárních titulů o vesmíru, teorii relativity a černých dírách, ale vše upovídané, bez srozumitelných výpočtů s vysvětlením matematického aparátu. Když to vezmeme sumárně za všechny oblasti, žádná sláva na nebesích.
Že nejvíc popularizační literatury vychází z matematiky je nasnadě. Píše se o ní nejsnáze. Pak je to již jenom otázka kvality toho kterého titulu. Nedávno se mi dostal zcela náhodou do ruky útlý titul Duch matematiky od Davida Achesona [1]. Knihu jsem prolistoval a zastavil se u kapitoly č. 26 s názvem Druhá odmocnina z minus jedné. V kapitole je zmíněn výsledný Cardanův vzorec pro obecné řešení kubické rovnice. Jak se k němu lze dopracovat je velice stručně uvedeno v poznámce na straně 169 a 170. Podle mě výpočet není až tak triviální, aby se odbyl tak stručnou poznámkou. A tak mi to nedalo, a řekl jsem si, že ten výpočet dám v souladu s doporučením v knize na papír, tedy ne zcela matematicky přesně, ale spíš populárně. Pokud stojíte o přesný výklad doporučuji kvalitní a komplexní titul [2].
Na obrázku č. 1 (číslo zjistíte po najetí kurzoru myši na obrázek) v bodě č. 1 je uveden tvar kubické rovnice, kterou budeme řešit, a výsledné řešení, které v textové podobě poprvé publikoval v roce 1545 Girolamo Cardano. Výsledek vypadá docela divoce, ale jak uvidíme, není to pokaždé až tak hrozné. Pokud jste si všimli, že v zápisu kubické rovnice chybí člen s x2, není to žádné opomenutí, protože kubická rovnice s kvadratickým členem se jednoduchou transformací dá převést na rovnici bez tohoto členu. Dále je na obrázku, body č. 2, 3 a 4, uvedeno vše, co budeme k řešení kubické rovnice potřebovat, vesměs se jedná o látku z prvního ročníku střední školy. Za připomenutí stojí Viètovy vzorce, které definují vztahy mezi koeficienty kvadratické rovnice a kořeny této rovnice. V dalším tyhle vzorce použijeme.

Na obrázku č. 2 je detailní postup řešení dle doporučení v titulu [1]. Jinak tento postup se zcela běžně používá při řešení kubické rovnice. Vtip je v tom, že řešení hledáme ve tvaru x = u + v, což nám dává určitou volnost při řešení, což také využijeme tím, že stanovíme podmínku 3uv = p. Tahle podmínka nám výrazně zjednoduší tvar řešené rovnice s proměnnými u a v a současně dostaneme Viètovy vzorce pro u3 a 3. Pomocí těchto vzorců sestavíme kvadratickou rovnici, v které položímě y = u3. Když spočteme neznámou y, tedy u3, pomocí vztahu v3 = q – u3 spočteme v3. A jelikož víme, že x = u + v, stačí u3 a v3 odmocnit. A je vymalováno. Tím bych měl úkol splněn.

Jenomže bez řešení konkrétní rovnice to není ono. Přece chceme vědět, jak se v praxi Cardanův vzorec používá. Z [2] jsem vybral na straně 103 z cvičení k řešení příklad č. 1, tedy ten nejsnadnější, přece nebudeme dřít jako tažné koně. U zadání příkladu je uveden výsledek, takže uvidíme, jak se nám bude dařit. Problém je, že naše řešení se neobejde bez elementárních znalostí komplexních čísel. Takže pokud vám to nic neříká, z řešení si prostudujte pouze úvodní dosazení do Cardanova vzorce a zbytek řešení vynechte.
Při řešení narazíme na jeden zásadní problém. Jak víme ze základní školy, druhá odmocnina např. z čísla 4 má dvě hodnoty, a to 2 a –2, neboť 2.2 = 4 a rovněž –2.–2 = 4. Tedy druhá odmocnina z jakéhokoliv čísla má dvě hodnoty. Třetí odmocnina tři hodnoty, např. třetí odmocnina z 27 je 3, neboť 3.3.3 = 27. Jenomže jaké jsou další hodnoty v tomto případě? Bohužel mají tvar, kde se vyskytuje komplexní jednotka i. Jaký je přesně tento tvar uvidíme za chvíli při řešení našeho příkladu. To je uvedeno na obrázku č. 3. Vidíme, že první kořen jsme hravě spočetli z Cardanova vzorce, vyšel nám 4. Že to platí, se odvodí dosazením x = 4 do rovnice x3 = 9x +28. Dostaneme 64 = 36 +28. Jenže jaké jsou další dva kořeny? V bodě č. 1 je uveden tvar třetích odmocnin z čísel 1 a 27. Ovšem i přesto ještě nemáme vyhráno, protože naše řešení musí splňovat podmínku u.v = 3, viz bod č. 2. Které kombinace čísel u a v tuhle rovnost splňují, je uvedeno v bodě č. 3. V tomto bodě je uvedeno i výsledné řešení naší kubické rovnice. Výsledek sedí, takže to vypadá, že jsme počítali správně.
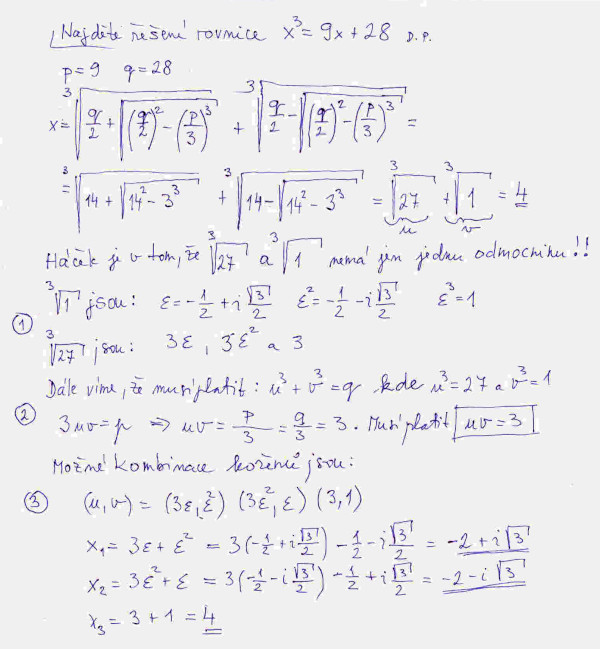
Když se podíváme na obecný Cardanův vzorec i výsledné řešení našeho příkladu kubické rovnice, je zřejmé, že výsledek se nám podařilo zapsat pomocí odmocnin, v takovém případě mluvíme o algebraickém řešení rovnic. Rovněž obecný vzorec pro řešení kvadratické rovnice obsahuje druhé odmocniny. Matematikům se podobné obecné vzorce, ač o hodně složitější, podařilo najít i pro řešení rovnic čtvrtého stupně. Věřili, že obecné řešení pomocí odmocnin se podaří najít i pro rovnice pátého stupně. Ale smůla, vždy to nejde, tedy univerzální vzorec není k dispozici. Koho více tahle problematika více zajímá, více o tom najde v [2] .
Ještě důležitá poznámka k řešení kubické rovnice. Už ze základní školy víme, o čem rozhoduje hodnota diskriminantu u řešení kvadratické rovnice. Pokud je kladný, tak kvadratická rovnice má dvě reálná řešení. Podobný diskriminant má i kubická rovnice, a dokonce také platí, že pokud je kladný, kubická rovnice má tři reálná řešení. Jenomže když hledáme tahle reálná řešení pomocí Cardanova vzorce, vyjdou nám imaginární čísla pod třetí odmocninou, a to je veliký problém. Jeden by si řekl, dobrá, vždyť pokud podobný případ nastane při řešení obecné kvadratické rovnice, jejíž koeficienty mohou být komplexní čísla, tedy vyjde nám imaginární číslo pod druhou odmocninou, lze známým vzorcem převést druhou odmocninu imaginárního čísla pod odmocninou na tvar a + bi, což vypadá jistě lépe než druhá odmocnina imaginárního čísla. Takže pokud nějakým šikovným trikem imaginární číslo pod třetí odmocninou převedeme na tvar a + bi, a když si uvědomíme, že Cardanův vzorec vykazuje symetrii, tak imaginární části se vynulují a zůstane nám reálné číslo. Bohužel bylo by to fajn, ale obecně to nejde. V určitých speciálních případech ano, ale obecně ne. V 16. století, v době kdy žil Cardano, korektní používání imaginárních čísel bylo velikou neznámou, něco se tušilo, ale více se tápalo, takže zmíněný případ matematici nazvali casus irreducibilis, tedy neredukovatelný případ. Otázka zní, je opravdu tento speciální případ neredukovatelný, tedy nemáme k dispozici postup, kterým bychom se dopracovali k reálným kořenům? Ale máme, je potřeba použít geometrický postup místo našeho algebraického! Pokud vás tahle problematika zajímá, opět doporučuji [2]. V každém případě casus irreducibilis významně napomohl k pozdějšímu zavedení komplexních čísel do matematiky. Jak říkají Číňané: Vše zlé je k něčemu dobré.
Použitá a doporučená literatura: [1] Acheson, D.: Duch matematiky, Dokořán, 2024. [2] Schwarz, Š.: Základy náuky o riešení rovníc (2. doplněné vydání), Bratislava, 1968, Vydavateľstvo SAV.
V Brně 25. ledna 2026.