O čekání
Dušan Polanský
Nebudeme si povídat o čekání na zázrak, na štěstí, na výhru v lotérii a tak podobně, ale tentokráte o obyčejném večerním čekaní na linku městské hromadné dopravy na jednom novém sídlišti v Brně. S večerním či nočním čekáním na MHD problémy nemám, jelikož moc pozdě po Brně nependluji, tedy s jednou výjimkou. Dcera bydlí v sídlišti Kamechy – pro ty, co nejsou z Brna, je to nové sídliště kousek před Žebětínem ve směru od Bystrce, no a Bystrc leží kousek od Brněnské přehrady –, a jelikož nejsem automobilista jezdím tam i zpět autobusou vou linkou č. 52. Večer po 20,00 hod. a přes víkend jezdí zmíněná linka v 20 minutových intervalech. Pokud si člověk nezjistí jízdní řád, klidně se mu může stát, že mu autobus ujede doslova před nosem a musí čekat dalších 20 minut, tedy pokud nevyužije linku 54, která jezdí rovněž každých 20 minut s linkou 52 proloženě. Ovšem trasa linky 54 je částečně jiná než linky 52, takže ne každému musí vyhovovat.
Mně problém s čekáním u linky 52 ale nehrozí, třebaže hodinky již dlouho nenosím. Odjezdy si pamatuji, od vnoučat odcházím tak, abych byl u zastávky asi 15 minut před odjezdem. Píšu schválně u zastávky místo na zastávce, jelikož těch 15 minut mám na vypití čtvrtky bílého vína ve vinotéce přesně oproti zastávce. Teď je to již v pohodě, jelikož pan vedoucí pověsil na zeď hezké kulaté nástěnné hodiny, předtím jsem čas odhadoval podle tempa popíjení vinného moku.
No a právě v jeden všední den po 20,00 hod. se stalo, že poté, co jsem si odbil svoji denní zdravotní dávku a přešel přes silnic na zastávku, uviděl jsem podél silnice nervózně popocházet starší paní. Hned se mě zeptala, zda již autobus pojede. „Jistě, pojede,“ odpověděl jsem, „ale obvykle má tak dvě minuty zpoždění, jednou měl dokonce šest minut.“ Dáma vyvrátila oči málem zoufale k tmavým bezhvězdným nebesům. „Já mám v životě na dopravu smůlu, všude čekám,“ pronesla vztekle. „Teoreticky by to mělo být tak, že pokud byste na zastávku chodila často a náhodně ve všední den po 20,00 hod. nebo o víkendech kdykoliv, aniž byste si pamatovala odjezd autobusu, průměrně byste čekala 10 minut.“ Moje pravděpodobnostní úvaha ji vytočila ještě více. „To pochybuji, mně to vždy ujede před nosem!“ Naštěstí dojel autobus a já nemusel ve svých teoretických úvahách pokračovat, jelikož hrozilo nebezpečí, že dámu vytočím ještě více. Také proto jsem si raději sedl na opačný konec téměř prázdného autobusu než dáma. A jak mě autobus vezl k našemu paneláku, napadlo mě napsat o podobném čekání matematický střípek.
Znalosti potřebné k pochopení výkladu jsou minimální. Problém může být, že budeme předpokládat elementární znalost integrálního počtu. Pokud jej neznáte, budete si muset odpustit estetický požitek z dvou malých důkazů.
Náš problém je prostý, ptáme se, jaká je průměrná doba čekání a směrodatná odchylka v případě intervalu odjezdů dopravního prostředku každých 20 minut. Předpokládáme čistě teoreticky, že cestující chodí na zastávku zcela náhodně, tedy bez jakékoliv znalosti jízdného řádu.
Podle popisu je to problém na tzv. spojitou náhodnou proměnnou, jelikož předpokládáme, že cestující může přijít na zastávku kdykoliv. Našemu myšlení je asi bližší pojem diskrétní náhodné proměnné. Příklad na takovou náhodnou proměnnou vidíte na obrázku č. 1.
Představme si, že se nudíme, a že po tisíc dnů, den co den, v stejnou dobu si zapisujeme počet chodců, kteří přejdou po chodníku před naším domem během určitého stejně dlouhého intervalu. Výsledky našeho pozorování jsme si uspořádali do tabulky, kterou vidíte nahoře. Diskrétní náhodná proměnná je počet chodců prošlých po chodníku před naším domem v pozorovaném intervalu. Nabývá hodnot: 0, 1, 2, 3, 4, 5, 6. Nikdo nešel ve 30 dnech, jeden chodec šel v 48 dnech atd. Vpravo je uveden vzoreček pro výpočet průměru diskrétní náhodné proměnné. Ten jsme spočetli v tabulce, výsledek je 4,208. Těžko si představit, že projde po chodníku 4,208 člověka, spíš si představíme, že průměrně to budou 4 chodci. Pro začátečníky označení P(X=x) čteme takto: diskrétní náhodná proměnná X nabývá hodnoty x. V našem příkladu proměnná X je počet chodců prošlých po chodníku před naším domem v pozorovaném intervalu a hodnoty x jsou: 0, 1, 2, 3, 4, 5, 6.

Druhou častou charakteristikou náhodně proměnné je rozptyl a z jeho odmocniny vypočtená směrodatná odchylka. Pro výpočet rozptylu jsou u druhé výpočtové tabulky uvedené dva vzorečky. První udává klasickou definici, druhý se hodí více pro praktický výpočet. Pokud jsme správně počítali, tak rozptyl je 2,587. Odmocnina z rozptylu je 1,608, což je hodnota směrodatné odchylky. Říká nám, jaké jsou průměrné odchylky hodnot náhodné proměnné vůči vypočtené střední hodnotě.
Jak se přepíšou zmíněné vzorečky pro výpočet střední hodnoty a rozptylu v případě spojité náhodné proměnné? Přechod od vzorečků pro diskrétní náhodnou proměnnou k vzorečkům pro spojitou náhodnou proměnnou je jednoduchý. Sumační znak se nahradí integrálem a P(X = x) tzv. hustotou pravděpodobnosti. Hranice spojité náhodné proměnné jsme označili řeckými písmeny alfa a beta. Tady jsou konečné, ale v praxi mohou být i nekonečné. Obsah plochy pod křivkou hustoty pravděpodobnosti je roven 1. To vyplývá z toho, že suma všech pravděpodobností náhodné proměnné musí být vždy 1.
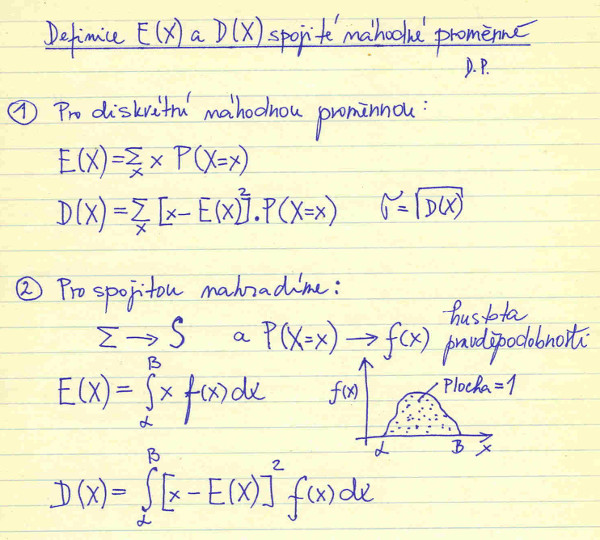
Konečně se dostáváme k řešení našeho problému s čekáním na zastávce. Abychom mohli vzorečky pro spojitou náhodnou proměnnou aplikovat potřebujeme znát dvě veličiny: hustotu pravděpodobnosti a interval, v němž se hodnoty spojité náhodně proměnné mohou vyskytovat. Interval je jasný z jízdního řádu (0;20). Horší by to mohlo být s určením hustoty pravděpodobnosti, ale opravdu jenom mohlo. Když si uvědomíme, že naše rozdělení pravděpodobnosti je rovnoměrné, jelikož cestující může přijít na zastávku kdykoliv v průběhu 20 minutového intervalu mezi odjezdy autobusů – proto mluvíme o spojité náhodné proměnné – a že plocha pod křivkou hustoty pravděpodobnosti musí být 1, není těžké „uhodnout“: že pokud základna je rozdíl (beta – alfa), tak výška – tedy hustota pravděpodobnosti – musí v intervalu (beta – alfa) být 1/(beta – alfa), aby nám plocha pod křivkou hustoty pravděpodobnosti vyšla 1. Mimo interval (beta – alfa) je hustota pravděpodobnosti nulová.
Teď už nám zbývá jenom spočíst střední hodnotu a rozptyl, potažmo směrodatnou odchylku pro spojitou náhodnou proměnnou v případě našeho rovnoměrného rozdělení. K výpočtu je potřeba znát vzorce pro výpočet třech integrálů, jež jsou uvedeny v rámečku. No a hlavně se pak nepomýlit při výpočtu. U výpočtu rozptylu jsem vypustil zbytek algebraických úprav kvůli místu. Přiznám se, že jsem se také chvíli potrápil, než jsem se trefil do předem známého výsledku.
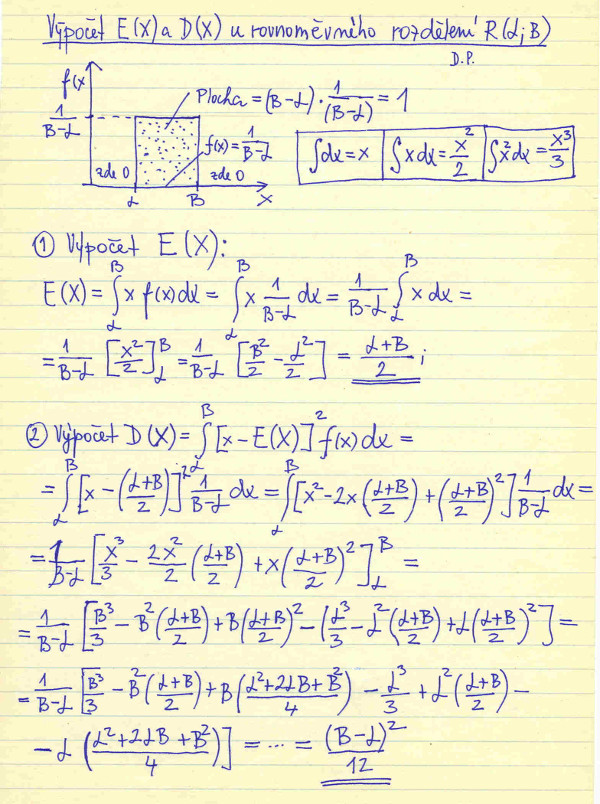
Dosaďme teď do obecných výsledků hodnoty z našeho popisu situace na zastávce u vinotéky! Střední hodnota je jasná, (0 + 20)/2 se rovná 10 minut. K stejnému výsledku bychom lehce došli i laickou úvahou bez našeho složitého výkladu. Rozptyl: 400 /12 =33,333. Směrodatná odchylka kolem střední hodnoty je odmocnina z rozptylu, v našem příkladu je odmocnina 5,773. Vidíme, že je poměrně veliká. Sice střední hodnota je 10 minut, ale nesmíme předpokládat, že pokud budeme chodit na zastávku často a opravdu náhodně, že doby čekání budou většinou těsně kolísat kolem 10 minut, nic takového nám výpočet neříká, spíš musíme počítat s tím, že rozptyl doby čekání vůči střední hodnotě bude značný, jak k delším dobám čekaní, což je nepříjemné, ale také ke kratším dobám čekání, což je zase příjemné. Tohle mohu potvrdit z vlastní praxe, když chodím v sobotu nebo v neděli již nějaký rok při cestě na zahrádku schválně pas blind na zastávku linky č. 50 a č. 52 u našeho paneláku a čekám, co pojede. Interval obou je rovněž 20 minut, ale obě linky jezdí těsně za sebou, takže lze v prvním přiblížení uvažovat, že jezdí jedna linka. Většinou čekám opravdu dlouho nebo krátce. Do středu se moc netrefuji. Ovšem pokud bych si doby čekání zapisoval a bylo by jich hodně, jejich průměr by se blížil k vypočtené střední hodnotě 10 minut.
Něco jiného by bylo, kdyby dopravní podnik neměl pevné jízdní řády, ale volné, přičemž by garantoval, že náš autobus jezdí v průměru např. každých 12 minut. Na první pohled by si cestující řekl, že průměrně bude čekat 6 minut. Kdepak, byl by překvapen, čekací intervaly by byly průměrně obvykle delší. Proč? Zkuste si nakreslit přímku a na ni zvislou čárou pět příjezdů autobusů. Nechť první dva jsou od sebe 8 minut, pak další zase 8 minut, pak 16 minut a opět 16 minut. Průměr čekacích intervalů je opravdu 12 minut (48/4), jak dopravní podnik slíbil, ale je jasné, že dlouhé intervaly zabírají na přímce delší úsečku, takže je i větší pravděpodobnost, že se trefíme do delší čekací doby. Někdy se tomuto jevu říká paradox autobusové zastávky, jak ale vidíme, o žádný paradox se nejedná. A to je vše.
V Brně 25. března 2015.