Metoda nejmenších čtverců
Dušan Polanský
A bavili jsme se o platech, tedy o jejich výši. Téma k pivu docela vděčné, třebaže ne tak jako počasí či ženské nebo vysoká politika. Ovšem platy a politika mají k sobě určitě blíže než prostitutka a její kunčaft. Dlouhodobě jsem názoru, že platy v státním sektoru by neměly předbíhat platy zaměstnanců v podnikatelské sféře, už jenom proto, že v státním sektoru mají zaměstnanci daleko větší jistoty. No a co si budeme povídat, pracovní nasazení jistě neodpovídá nasazení v soukromém sektoru. Důsledkem téhle nelogické mzdové politiky je, že to pak žene nahoru mzdy i v soukromém sektoru a finálně to vede k zdražení všeho, tedy i piva, u něhož jsem se o platech bavili. A když už jsme u platů, u těch by se neměl už jenom ze slušnosti uvádět průměrný plat. Když už tak medián, u toho platí, že 50 % platů je menších nebo rovných mediánu a 50 % hodnot je větších než medián. Medián alespoň trochu ukazuje rozsah tunelování finančních prostředků managementem, protože není ovlivněn ani velmi malými, ani velmi velkými hodnotami. Naopak průměrný plat je těmito hodnotami ovlivněn docela výrazně.
Je to už nejméně 5 let, co mi ukazoval jeden doktorand, inženýr ekonom, jakési svoje odborné pojednání k platům, a aby to vypadalo učeněji pochopitelně tam nasáčkoval i matematiku, kromě jiného i tzv. lineární regresi (neděsit se, viz dále). Vysvětlil jsem mu důvody své skeptičnosti k podobným kouzlům s matematikou, ono totiž také matematika je někdy děvka pro všechno, zvláště obor zvaný statistika (úsměvně: exaktní věda o přesném počítání s nepřesnými údaji). Když někdo píše kupříkladu doktorandskou práci z ekonomie, tak do ní obvykle nastrká vzorců a modelů více než požehnaně. Důvod je prostý: pojednání musí působit dojmem exaktnosti! Jenomže ekonomika je společenská věda, a v takových aplikovat matematiku smysluplně je určitě těžší než v přírodních, biomedicínských a technických vědách, i proto snahy o matematizaci společenských věd působí většinou dost uměle, někdy až úsměvně.
Ale než se vrátíme opět k platům a matematice, mala poznámka k požadovaným znalostem pro pochopení dalšího textu. Budeme si povídat o odhadu parametrů charakterizujících regresní přímku (viz dále) spočtenou metodou nejmenších čtverců. Příslušné vzorečky lze odvodit i bez vyšší matematiky, tedy v našem případě znalosti diferenciálního počtu, ale přesto zde tento počet použijeme, důvodem je elegantnost výpočtů a možná že, pokud máte averzi k matematice, že vás naše povídání namotivuje k tomu, že se začnete o ni trochu zajímat. Ale i ti, kdo základy tohoto počtu nemají, nemusí zoufat, pointu si vysvětlíme laicky. A nakonec všechny detaily výpočty nebudu beztak uvádět, jelikož jsou k nalezení v každé slušnější učebnici statistiky. Praktický výpočet parametrů regresní přímky si ukážeme v Excelu. Text se vám bude určitě lépe číst, pokud máte alespoň elementární znalost teorie pravděpodobnosti.
O co nám vůbec půjde? Jednoduše řečeno budeme se zabývat lineární závislostí náhodné veličiny Y na veličině X, která náhodná není. Slovíčko lineární závislost říká, že tahle závislost by měla být lineární, tedy graficky se alespoň přibližně podobat přímce. My coby příklad použijeme již zmíněné platy, alespoň uvidíme, jak to dopadne. Náhodnou proměnou v našem příkladu budou platy, nenáhodnou veličinou budou jednotlivé kalendářní roky. Na stránkách Českého statistického úřadu jsem si vyhledal údaje o nominální mzdě od roku 2001 do roku 2015, ovšem k výpočtu parametrů zmíněné přímky použijeme pouze roky 2001 až 2010, pokud jde o roky 2011 až 2015 ty podle dotyčné přímky odhadneme, no a nakonec porovnám s tím, co nám sdělují státem placení statistici, kteří jako vzorní lokajové neradi zveřejňují medián, viz poznámku výše.
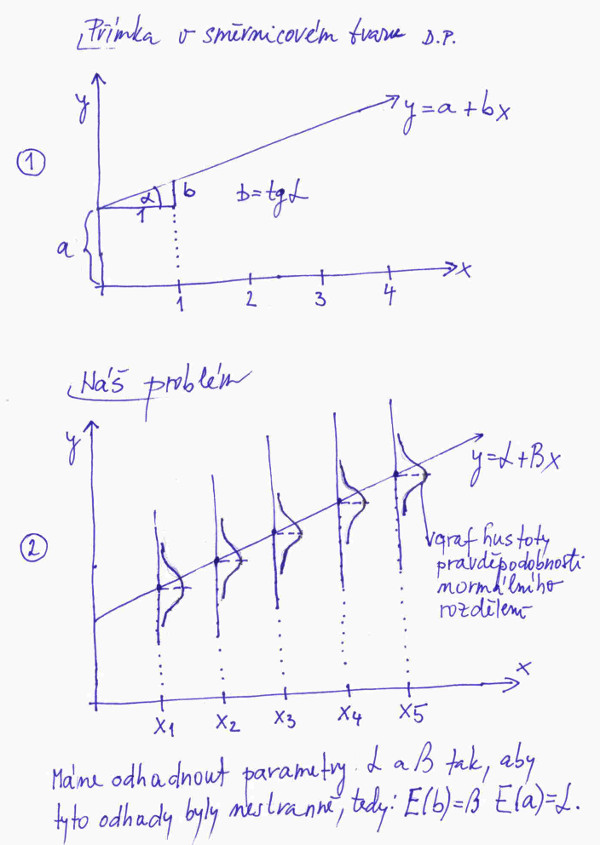
Rovnice přímky v tzv. směrnicovém tvaru se ve škole obvykle píše ve tvaru y = kx + q. Jak již víme z posledního ročníku základní školy q je bod, v němž přímka protíná osu y a k je směrnice, která nám říká, jaký sklon má přímka vůči ose x neboli jaké stoupání je na jednotku délky nezávislé proměnné. Předesílám, že v statistice se obvykle používá formálně trochu jiný zápis rovnice regresní přímky, a to y = a + bx, tohoto zápisu se budeme držet i my, viz obrázek č. 1, bod č. 1. Číslo obrázku zjistíte po najetí myší na obrázek.
Poměrně jednoduše se jádro toho, k čemu se chceme dopracovat, vysvětluje na měření nějaké fyzikální veličiny, která je lineárně závislá na nějaké nezávisle proměnné, např. ze základní školy známe Ohmův zákon, pomocí něhož dokážeme graficky znázornit závislost proudu na napětí při konstantním odporu. Jenomže kdybychom provedli měření nachlup přesnou přímku asi nedostaneme, protože každé měření není nikdy úplně přesné kvůli drobným chybám (přesnost samotné metody měření, přesnost přístroje, přesnost odečtu lidským okem potažmo elektronického odečtu, vliv podmínek při měření atd.). Na výsledné hodnoty jednotlivých měření působí součet mnoha malých vlivů. Ještě složitější pravidla platí při měření v kvantové mechanice, ale tyhle složitosti teď nechme stranou. Takzvaná centrální limitní věta (na tu jsou matematici docela pyšní) dokazuje, že součty mnoha malých vlivů jsou normálně rozděleny; někdy říkáme, že mají Gaussovo rozdělení. Podrobný důkaz této slavné věty lze nalézt v každé jenom trochu slušně napsané knize o teorii pravděpodobnosti. U náhodného rozdělení křivka hustoty má tvar zvonu. Kupříkladu normální rozdělení má výška dospělých mužů nebo žen, roční srážky v mm v Brně, IQ všech lidí v ČR, rychlost aut jezdících kolem božích muk po rozbité silnici okresní třídy.
Protože předpokládáme lineární závislost a pokud zaznamenáme naměřené údaje do grafu, pak na první pohled by mělo být vidět, že se nimi dá proložit přímka, která by měla vyjadřovat onu lineární závislost. Ovšem jak ji proložit? Od oka nebo si vzít na pomoc matematiku? V každém případě, abychom takovou přímku mohli do našeho grafu nanést, potřebujeme znát dva parametry přímky: a a b. No a tom, jak určit tyhle parametry si budeme povídat.
Nepatrně více učeně si vše můžeme představit podle bodu č 2. na obrázku č. 1. Vidíme zde nakreslenou regresní přímku, jak by měla vypadat zcela ideálně, proto jsme její rovnici napsali ve tvaru: y = alfa + beta*x. Ideální přímka by měla procházet vrcholy zvonů náhodného rozdělení jednotlivých měření. Jde totiž o to, že metoda nejmenších čtverců je nejvhodnější v tom případě, kdy hodnoty x1, x2 ... známe přesně a k chybám dochází pouze při určování y1, y2 ..., a navíc tyto chyby musí být navzájem nezávislé a mají stejné Gaussovské rozdělení.
Naším úkolem bude odhadnout parametry alfa a beta, tak aby tyto odhady, označíme je a a b splňovaly podmínku tzv. nestrannosti, tedy že pro střední hodnoty parametrů platí: E(a) = alfa, E(b) = beta.
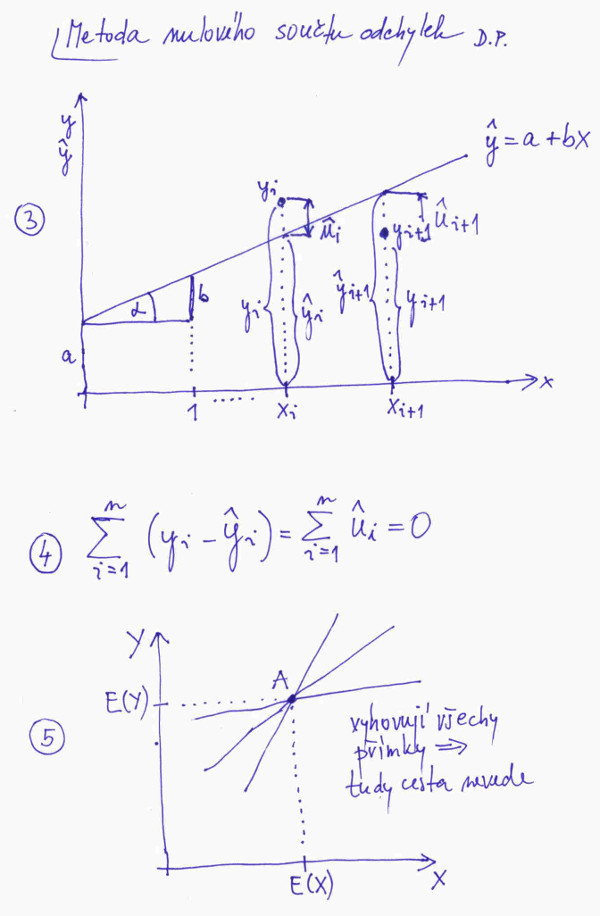
Takže teď před námi stojí problém nalezení parametrů a a b regresní přímky. Podívejme se na obrázek č. 2, bod č. 3. Vidíme zde nakreslenou situaci pro dvě hodnoty nezávislé proměnné xi a xi+1. Hodnoty náhodné proměnné jsou označeny yi a yi+1. Odchylky jsme označili ui a ui+1. Dále si jenom orientačně proložme body (xi, yi) až (xn, yn) regresní přímku, jakože už její rovnici známe. Hodnoty závislé náhodné proměnné na této přímce značíme stříškou.
Můžeme intuitivně uvažovat takto: přímku by bylo vhodné přeložit tak, aby suma odchylek náhodné veličiny Y od regresní přímky byla nula, přičemž odchylky nad regresní přímkou budeme brát se znaménkem plus, pod přímkou se znaménkem mínus, viz bod č. 4. Z ne moc složitého výpočtu pak plyne, že taková přímka by měla procházet aritmetickými průměry nezávisle a závisle proměnné, viz bod č. 5. Ovšem jaký sklon, tedy směrnici má mít přímka? Libovolný, tedy kromě vertikály, která beztak nemá v našem problému analogii v realitě! Proč libovolný? Když přímku natočíme jakkoliv, z hlediska sumy velikosti všech odchylek od přímky se nic podstatného nestane. Když se vlevo od bodu A odchylky posunou o jakési hodnoty, tak napravo od bodu A se posunou přesně opačně a kritérium v bodě č. 4. bude stále splněno.
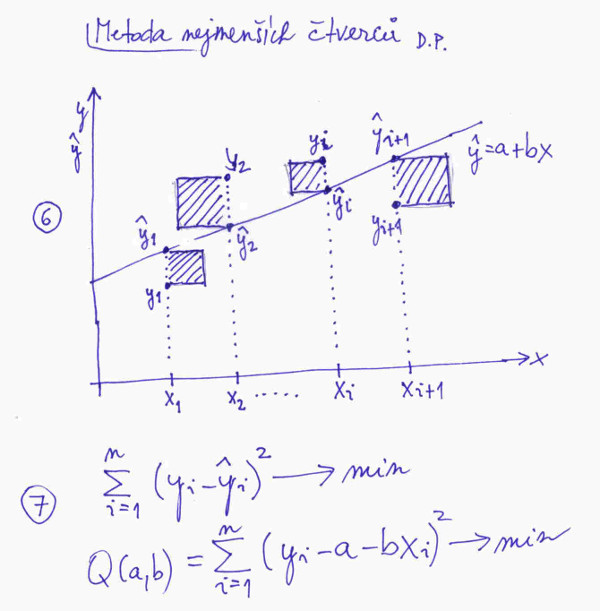
Již z této úvahy vidíme, že pracovat s pouhým součtem odchylek nikam nevede. Co s tím? Zbavit se nějak šikovně znamének odchylek. Určitě to nepůjde tak, že všechny odchylky budeme brát s kladným znaménkem. To bychom se nikdy k žádnému rozumnému minimu odchylek od regresní přímky nedopracovali. Ovšem z matematiky víme, že znamének se lehce zbavíme umocněním na druhou, např. -2 na druhou je 4, stejně jako 2 na druhou. A co jsme vlastně v obou případech geometricky spočetli? Jistě, obsah čtverce o straně 2, přičemž je nám jedno, zda čtverec leží nad nebo pod regresní přímkou. Regresní přímku se budeme snažit proložit tak, abychom minimalizovali obsah čtverců, situaci vidíte na obrázku č. 3, body č. 6. a 7. A to je i myšlenka metody nejmenších čtverců.
Analogickou situaci známe např. z teorie pravděpodobnosti. Pokud spočteme střední hodnotu náhodné proměnné X, značí se obvykle E(X), a spočteme součet E(X -E(X)) pro všechny hodnoty náhodné proměnné, vždy dostaneme 0, což nemusí vždy vyhovovat, jelikož naprosto nic se nedozvíme o rozptylu náhodné proměnné kolem střední hodnoty. A právě proto, tedy pro charakteristiku rozptylu hodnot náhodné proměnné kolem střední hodnoty, se používá rozptyl (disperze) D(X) = E(X -E(X))2, potažmo druhá odmocnina z rozptylu, tzv. směrodatná odchylka. A hle v rozptylu nám také vystupuje druhá mocnina!
Teď už když víme jak na to, stačí spočíst parametry a a b regresní přímky. K tomu se obvykle používá diferenciální počet více proměnných (proměnné jsou v našem příkladu dvě: a, b). Na obrázku č. 4. jsem naznačil pouze postup výpočtu. Těm, co diferenciální počet více proměnných znají, bude postup výpočtu pravděpodobně jasný, těm, co neznají, musí uvěřit, tak jako první křesťané uvěřili, že Ježíš je Kristus. Vzdělaný teoretický matematik by jistě poznamenal, že funkce Q(a,b) musí splňovat důležité podmínky. Ano, měl by pravdu, ale my si jenom řekneme, že tyhle podmínky splňuje.

Když to vše shrneme: výhodou Gaussovy přímky je, že její rovnici lze nalézt poměrně snadno. Prochází bodem, který má za souřadnice aritmetický průměr hodnot X a aritmetický průměr hodnot Y. Sklonem je tzv. Bravais-Pearsonův korelační koeficient násobený standardní odchylkou proměnné Y a vydělen standardní odchylkou proměnné X. Také lze dokázat, že přímka vypočtena metodou nejmenších čtverců je za určitých okolností v určitém smyslu nejlepší aproximací správné, ale neznámé přímky. Tato vlastnost je ve statistice známa jako Gauss-Markovova věta.
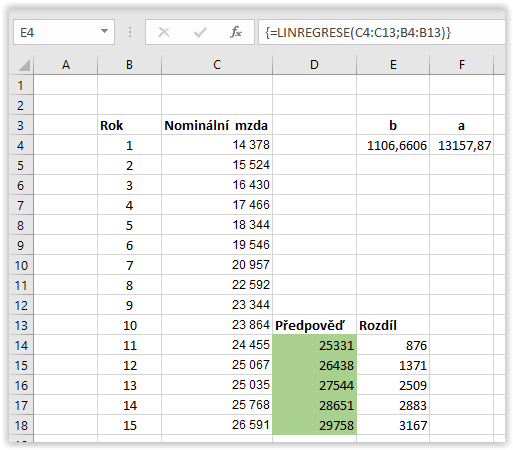
Metoda nejmenších čtverců se v Excelu skrývá pod funkcí LINREGRESE. Praktické použití této funkce si ukážeme na již zmíněných platech. Na obrázku č. 5 je výřez listu Excelu. V buňkách B4 až B18 jsou uvedeny údaje Českého statistického úřadu o nominálních platech v letech 2001 až 2015. Ovšem k výpočtu regresní přímky použijeme pouze platy v letech 2001 až 2010, platy v letech 2011 až 2015 odhadneme z regresní přímky, viz buňky D14 až D18 (jsou zeleně podbarvené). Vidíme, že rozdíly mezi předpovědí a realitou – jsou uvedeny v buňkách E14 až E18 – jsou poměrně veliké. Ovšem jak je všeobecně známo, a je to vidět i z údajů ČSÚ, v letech 2011 až 2015 platy relativně stagnovaly, kdežto platy v letech 2016 až 2018 dost výrazně rostly, takže rozdíly mezi předpovědí a realitou by v posledních třech letech byly určitě menší. Jinak koeficient b má velice názorný význam, říká nám, o kolik by platy měly za rok v průměru narůst. Koeficient a regresní přímku pouze polohuje v rovině.
Teď krátce k praktickému použití excelovské funkce LINREGRESE v našem příkladu. Nejprve si označíme buňky E4 a F4, poté napíšeme do nich vzorec =LINREGRESE(C4:C13;B4:B13). A teď přijde to důležité, současně stiskneme klávesy Ctrl + Shift + Enter, do vzorce se automaticky doplní složené závorky a provede se výpočet parametrů a a b. Složené závorky nám říkají, že se jedná o maticový vzorec. Maticový vzorec proto, že pracujeme s maticemi (poli) C4:C13 a B4:B13. Jinak povídání o maticových vzorcích lze nalézt v každé příručce Excelu.
Závěrem úvaha k náhodnosti výše platů. Typickou náhodnou proměnnou by byly, kdyby opravdu jejich výši určoval jenom trh, jelikož ten je za normální situace (tedy bez válek, obrovských přírodních katastrof atd.) ovlivněn mnoha malými vlivy, přesně tak, jak to požaduje centrální limitní věta. Je sice pravda, že trh pozná nejen období prosperity, ale i období recese, kdy platy minimálně stagnují, ale tohle by se za normální situace v dlouhodobém časovém úseku nemělo na výši platů zásadní vliv. Bohužel dokonalý trh je fikce. Zásahy politiků do mzdové politiky jsou někdy tak významné, že o malých vlivech těžko mluvit, což předpoklad normálního rozdělení zpochybňuje. Kupříkladu v současném období došlo k dost nelogickému prudkému navýšení platů v státní sféře. Ale budiž, ať se mají dobře, koneckonců v našem povídání nám o platy vůbec nešlo, cílem bylo vysvětlit si metodu nejmenších čtverců. Pokud se mi to alespoň trochu povedlo, cíl byl splněn. Pokud ne, i tak dobře, zvědavce to snad motivuje k hlubšímu zamyšlení a znalosti si hravě nejen doplní, ale i rozšíří v bohaté literatuře o teorii pravděpodobnosti.
V Brně 17. března 2019.