D’Alembertův princip setrvačných sil

Dušan Polanský

Mám rád obecné zákony, principy, které máme na očích málem všude a neustále, ale uspěchaný život, běžné starosti, způsob výuky na školách, nezájem či nezajímavost z našeho pohledu nám nedovolují vychutnat jejich krásu, hloubku a eleganci. Takovým zákonem je pro mne i D’Alembertův princip setrvačných sil. Pokud nemáte fyziku v lásce, neděste se, tenhle princip pod mým nepedagogickým vedením jistě pochopíte, tedy alespoň si to myslím. Ovšem praktické hluboké zvládnutí tohoto principu v složitějších případech je někdy rébusem i pro kované fyziky. Pokud jde o vstupní vědomosti, bohatě vystačíme s učivem základní školy. Koneckonců jakákoliv fyzikální teorie - má li učitel (tím nejsem) ji poctivě a hluboce zvládnutou - dá se většinou vyložit bez složitého matematického aparátu. A pokud takový aparát je nezbytný, dá se i ten vtipně, logicky a hlavně srozumitelně vysvětlit, opět za předpokladu, že jej přednášející do hloubky zvládnul. Jestli tomu tak není, tak popularizační výklad dopadne s velikou pravděpodobností nevalně. Dokladem téhle bídy jsou i desítky popularizačních knih z matematiky a fyziky, z nichž se dozvíte jenom obecnosti a autor vám neustále opakuje, že problém je moc složitý a potřeboval by na výklad více místa. A takhle fňuká např. na 270 stránkách textu a navíc vás otravuje obecnostmi a popisy pohnutého života příslušného objevitele a poměrů za jeho života. Neopomene přidat výčet jeho přátel i nepřátel a výklad vztahů s nimi. Čert ber takové pisálky!

Proč tohle popularizační odborné povídání skončilo v střípcích a ne v článcích, kam občas nacpu i nějakou tu odbornou drobnost? Důvody jsou tři. Nedávno jsem byl ve vinotéce náhodným svědkem vášnivé diskuze starších pánů – cca 70 let a více – ohledně bezpečnosti výtahů. Až jsem se divil, co za fyzikální zákony stihli u vína vymyslet! Do jejich vášnivé diskuze jsem nevstoupil. Proč zrovna já, neučitel, bych jim měl opět vysvětlovat učivo základní a střední školy? Maximálně bych jim mohl doporučit, aby požádali ministerstvo školství o vrácení školného. Leč všechno zlé je na něco i dobré. Poslouchaje je, jsem se rozhodl, že napíšu střípek, kde ten zatracený výtah a nějaká ta dynamika bude. Druhý podnět je z videa promítaného v prostředcích MHD v Brně. Video se mi moc líbí. Je o bezpečnosti cestujících při cestování prostředky MHD. Názorně ukazuje, jak je důležité se při jízdě pořádně držet a jak se má maminka s kočárkem správně postavit, aby zajistila bezpečnost nejen dítěte, ale i svoji. Nedávno jsem jel autobusovou linkou 50. Byla v něm i maminka s kočárkem. Postavila se s kočárkem přesně opačně než měla. Správně se má maminka opírat zády o bezpečnostní opěradlo. Rovněž dítě by mělo sedět zády k řidiči. A jako naschvál skočil pod autobus neodpovědně hlídaný pes. Prudké zabrzdění a kočárek s dítětem prudce narazil do bezpečnostního opěradla a s malou holčičkou to pořádně hodilo směrem dopředu. Vše nakonec dopadlo dobře, ale nemuselo. Bylo by to bývalo zcela zbytečně moc smutné. Holt někdy se vyplatí znát i takovou „zbytečnost“ jako je setrvačná síla. Třetí důvod má co dělat s moji ješitností. Přirozený, neokázalý, přitom logicky jasný výklad jakékoliv učiva mi na školách všech stupňů až moc často chyběl. A tak, i když nejsa učitel, jsem se o něco takového chtěl pokusit alespoň na malém kousku fyziky. Takže, prosím, nastupte si do výtahu nebo dopravního prostředku a začínáme.

Princip, o němž si budeme povídat, publikoval v roce 1743 Jean Baptiste Le Rond d'Alembert (1717-1783), francouzský matematik a fyzik, osvícenský filosof, člen francouzské, berlínské a petrohradské akademie věd. A to nám bohatě, pro jakýs takýs historický kontext, o autorovi onoho principu stačí znát.

Pro pochopení celého výkladu je důležité vědět, co je to setrvačná síla a jak se v praxi projevuje. Není to žádná exotická síla, je to síla, která nutí setrvávat každé těleso v stave v jakém se před působením nějaké aktivní síly nachází. V některých starších učebnicích nebo sbírkách příkladů se nešťastně nazývala doplňková síla. Příklad z praxe. Jedeme v tramvaji uhánějící konstantní rychlostí, najednou řidič z vážného důvodu prudce zabrzdí. Co se stane? Především tramvaj se stane z inerciální vztažné soustavy tzv. neinerciální vztažnou soustavou, jelikož již se nepohybuje rovnoměrnou rychlostí, což je vlastnost newtonovské inerciální soustavy (na einsteinovskou máme přísnější požadavky). Aktivní brzdní síla působí proti směru jízdy tramvaje, ovšem stojící cestující a cestující sedící po směru jízdy, pokud se pořádně nedrží, padají jako shnilé hrušky, někdy i letí, ve směru jízdy tramvaje, tedy dopředu. Ať tramvaj před šlápnutím řidiče na brzdu jede rychlostí 50 km/hod, to je i rychlost cestujících vůči přihlížejícímu pozorovateli stojícímu na chodníku (tento pozorovatel nás pozoruje z inerciální vztažné soustavy, tou je povrch zemský, učeně geocentrická vztažná soustava). Při prudkém zabrzdění se prudce sníží rychlost tramvaje v důsledku brzdného zrychlení působícího proti směru jízdy tramvaje. Jenomže my cestující i samotná tramvaj chceme podle zákona setrvačnosti „setrvat“ v pohybu 50 km/hod vůči pozorovateli na chodníku. Síle, která nás nutí „setrvat“ v původním pohybu a tím způsobí naše padání ve směru jízdy tramvaje, říkáme setrvačná síla. Taková síla může vzniknout jenom v neinerciální soustavě, takovou je každá soustava, jež se pohybuje zrychleně vůči nějaké inerciální soustavě, což je soustava, která je v klidu nebo se pohybuje rovnoměrnou rychlostí. Když se tramvaj pohybuje rovnoměrnou rychlostí, žádná setrvačná síla na cestující nepůsobí, i kdyby se cestující nedržel, neupadne, což je ale z bezpečnostních důvodů zakázáno.

Z fyziky víme, že síla je součinem hmoty a zrychlení, které tělesu dotyčná síla udělí, tj. F = m.a. Síla je vždy síla, proto i pro setrvačnou sílu musí platit stejný vztah, tj. F_s = m.a. Jedině čím se liší od síly aktivní, je její směr, ten je přesně opačný. Proto se doporučuje děti posadit tak, tedy pokud tu možnost máme, aby seděly zády ke směru jízdy. Setrvačná síla je při prudkém zabrždění přitlačí k opěradlu, což je stále lepší, než padat celým tělem ve směru jízdy, což se děje v autech. Nakonec proto používámne bezpečnostní pásy. Z hlediska bezpečnosti cestujícíh by proto bylo lepší, kdyby všechna sedadla kromě sedadla řidiče byla orientována proti směru jízdy. Jenomže zase by utrpěl požitek z jízdy. V životě je vždy něco za něco.

Na rozběh ještě jeden drsný příkladík. Zavařili jsme „přátelům“, ti se nás na oplátku rozhodnou vyhodit z letícího letadla. Aktivní síla je zde jediná F_akt = m.g, tj. součin naší hmotnosti a gravitace. Z hlediska soustavy spojené s naším tělem, působí na nás nulová síla neboť obě síly, aktivní i setrvačná, jsou stejně veliké, tj. F_akt = F_s s síla F_s má opačný směr než síla aktivní. Opravdu za letu necítíte kromě psychického děsu a hrůzy z nehezkého konce pozemské pouti žádný tlak, tah nebo ohyb, tedy když zanedbáme odpor vzduchu. Ovšem vyhráno nemáme, z pohledu pozorovatele stojícího na povrchu zemském, ten je pro nás počátkem vztažné inerciální soustavy, naše maličkost je přitahována k zemi gravitační silou G = mg a naše rychlost při dopadu na Zem bude dána druhou odmocninou z výrazu 2.g.h (h je výška letu letadla od povrchu zemského), tedy pokud naši "přátele" byli tak slušní, že nás z letadla nevyhodili jako shnilé jabko, ale jenom "lehce" popostrčili. Ale na tuhle slušnost bych nevsadil ani korunu.

Pan d'Alembert možná nějak takhle všelijak uvažoval a nakonec v roce 1743 vyslovil princip podle něhož součet aktivních sil (v našem předchozím příkladě síla prudce brzdící tramvaj) a setrvačných sil (v stejném příkladě síla nutící tramvaj i cestující se pohybovat nadále stejnou rychlostí i po zahájení procesu brzdění) působích na těleso v neinerciálních soustavách je nulový. Formálně zapsáno: F_akt + F_s = 0. Při výpočtech nesmíme zapomenout zohlednit směr působení sil příslušným znaménkem, buď kladným nebo záporným. Volba kladného směru je na nás.

D’Alembertův princip má jeden dalekosáhlý a praktický důsledek pro praxi. Brzdící tramvaj je dynamická soustava, neboť je v pohybu, kdežto v statice, části mechaniky, se vyšetřují účinky působení aktivních sil na tělesa, která se i přes působení vnějších sil nepohybují. Když to nedopadne v statice dobře, tak se statické těleso působením aktivních sil zdeformuje a když to dopadne zcela zle, tak se zbortí a je z toho pěkný průšvih pro statika. V statice jsou podmínky rovnováhy tělesa velice jednoduché. Aby se neporušila „statika“ soustavy, musí být součet všech vodorovných i svislých sil působících na těleso roven nule. Podobný zákon platí pro součet momentů k libovolnému bodu statického tělesa. Kdyby k nějakému bodu tělesa moment nebyl nulový, tak by se těleso začalo otáčet nebo působením momentu sil deformovat. Když si uvědomíme, že F_akt + F_s = 0, tak d'Alembertův princip převádí úlohy dynamiky, tj. problém pohybu na jednodušší statický problém. V statice požadujeme, aby součet sil a momentů byl nulový a d'Alembertův princip požaduje něco podobného: chce aby součet aktivních a setrvačných sil v neinerciální vztažné soustavě byl nulový! Je ale důležité si uvědomit, že na rozdíl od statiky představa rovnovážného statického stavu dynamické soustavy je fiktivní! Rovnovážný stav z pohledu pozorovatele ve vztažné inerciální soustavy (v našich příkladech to bude pozorovatel stojící v klidu na zemském povrchu) nikdy nenastane. Před vyslovením d'Alembertova principu takovéto obecné pravidlo známé nebylo, a tak se dynamické problémy řešily případ od případu. Uplatňoval se vtip a tvořivost. Jean d'Alembert nám říká: jaképak copak, počítejte pomocí mého principu dynamické problémy jako kdyby to byly problémy statické, statičnost zajistíte tím, že do soustavy zahrnete i setrvačné síly. Takže držme se jeho rady, a vyzkoušejme si jeho doporučení na třech jednoduchých příkladech. Všechny jsem vám naškrábal vlastní rukou.

Abychom oba případy našeho prvního příkladu vyřešili, musíme si uvědomit směr setrvačné síly. V případě A působí směrem dolu, neboť my se rozjíždíme směrem nahoru a předtím byl výtah v klidu. A jak víme setrvačná síla by nás chtěla udržet v tomto nepohyblivém stavu. V případě B to bude přesně opačně, tj. působí směrem nahoru, jelikož aktivní síla směrem dolu. Když jsme si zakreslili správný směr setrvačných sil, další výpočet bude již jednoduchý, stačí pamatovat na to, že součet všech sil, včetně síly setrvačné, musí být nulový. Písmenem G jsme si označili gravitační sílu m.g, kde m je hmotnost výtahu i s cestujícími a g gravitační zrychlení.

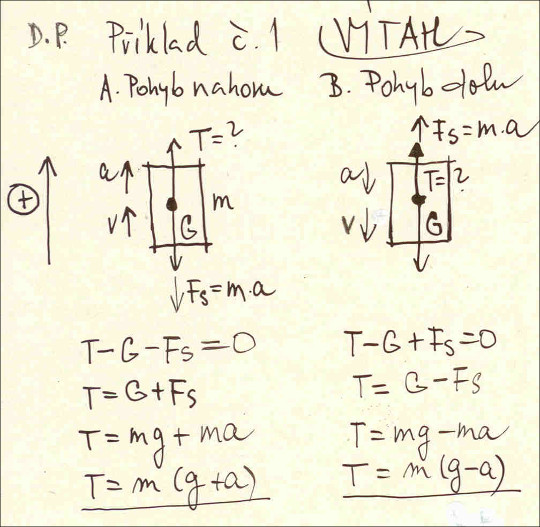
Je důležité umět vzorečky nejen logicky odvodit, ale i správně interpretovat neboli fyzikálně číst. V případě A nám výsledný vzoreček také říká, že náš tlak na podlahu výtahu bude větší, než kdyby byl výtah v klidu. V případě B naopak bude menší. O co? O zrychlení a.

Nejdříve si musíme uvědomit jaký bude směr setrvačné síly a pak napsat podmínku rovnováhy. Jediná aktivní síla v soustavě je váha břemena F_akt = m.g. Setrvačná síla působící na břemeno m, označíme si ji F_SB, bude směřovat vzhůru, protože celá soustava se pohybuje směrem dolu se zrychlením a. Ovšem v námi vyšetřované soustavě to není jediná setrvačná síla. Setrvačné síly budou působit i na břemena m₁ a m₂. Velikost těchto setrvačných sil bude m₁.a a m₂.a Směr je zcela jasný, také se jim nechce padat zrychlením a. Při zápisu podmínky rovnováhy musíme akceptovat zvolenou znaménkovou konvenci a započíst všechny setrvačné síly. Tentokrát kladný směr je zvolen směrem dolu.

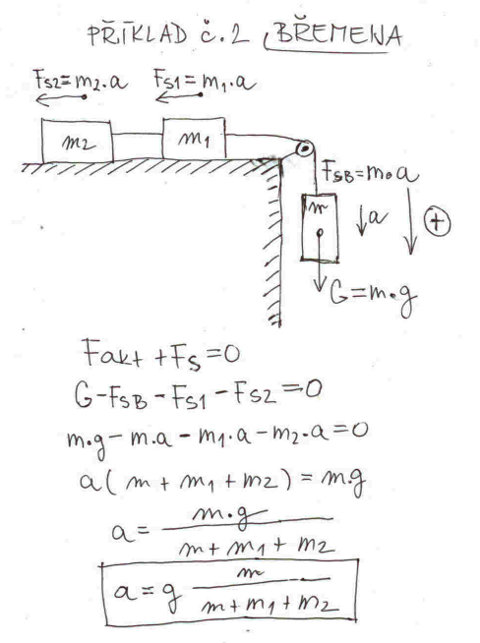
Výsledný vzorec nám říká, že se jedná o rovnoměrně zrychlený pohyb, neboť jak g i podíl hmot jsou konstanty. Pokud m₁ + m₂ = m, tak a = g/2. Pokud by břemena m₁ a m₂ byla nulová, břemeno m by padalo volným pádem, tj. a = g. Vidíme, že náš vzorec funguje i v tomto speciálním případě. Zdá se, že d'Alembertův princip jsme aplikovali na danou dynamickou soustavu správně.

Přeji vám hezké fyzikální sny, v nichž budete hravě řešit složité dynamické soustavy. Koneckonců i náš život je složitou dynamickou soustavou. Někdo si řekne, že by bylo dobře, kdyby i pro život existoval jednoduchý princip, jehož dodržování by nám zabezpečilo trvalé životní štěstí a trvalou pohodu. Ale raději ne, život bez proher, trápení, smutku, přiměřené hmotné nejistoty, snění o štěstí a hledání vlastních pravidel života a pravd o něm, by také za moc nestál. Pročež ani tak oslavované nebe, nemusí být vždy to pravé ořechové.

V Brně 13. listopadu 2012.

Dovětek. Starší pán mi napsal, že mu není jasné, zda setrvačné síly jsou skutečné nebo fiktivní, smyšlené. Uvádí příklad závaží zavěšeného na niti v pevném bodě a opisující kružnici se středem v tomto pevném bodě. Obvodová rychlost závaží je konstantní. Jeho argumentace je takováto: na závaží působí síla dostředivá, ta je jistě skutečná, kdyby totiž nepůsobila, těleso by uletělo do prostoru. Na závaží působí také odstředivá síla, a pokud i ta je skutečná, tak její velikost je stejná jako síly dostředivé, akorát má opačný směr. Takže ve výsledku na závaží nepůsobí žádná síla. To ale rozhodně pravda není! Zkuste si ale sednout na kolotoč. Odstředivá síla vás bude vynášet z kruhu ven. Kde je v úvaze chyba? V tom, že naše soustava se skládá ze dvou těles: závaží a nitě. Ty na sebe působí podle zákona akce a reakce. Niť působí na závaží dostředivou, závaží na nit odstředivou silou. Odstředivá síla nepůsobí přímo na těleso, ale nejprve na nit! Je zřejmé, že nit se může pod účinkem veliké odstředivé síly přetrhnout.

Vidíme, že setrvačné síly v neinerciálních soustavách skutečně existují, a tedy i působí, takže nejsou to žádné umělé výtvory fyziků, viz např. i naše povídání o tramvaji.

V Brně 13. ledna 2013.

Domů | Prolog 2001: Vesmírná odysea | Nejen básně v próze | Střípky