Něco málo o derivaci
Dušan Polanský
Moralistický úvod
S výukou školního předmětu matematika - bez ohledu na reformy, nové trendy ve výuce apod. - je to s jako výukou každého jiného školního předmětu. Buď je učitel dotyčného předmětu dobrý učitel, nebo nedobrý. Ten první učí s láskou, srozumitelně, názorně, poutavě a někdy, když je to třeba, i trpělivě. Ten druhý učí obvykle s odstupem, suše, nejednou ne příliš srozumitelně a názorně, nerad se ve výkladu opakuje a obvykle je velice přísný v hodnocení, a navíc má o sobě vysoké mínění, pak se ovšem divím, že se nevydal na jinou profesní dráhu. Ve svém školním životě každý z nás potkal jak ty první, tak i ty druhé učitele. Nechci další výklad dávat za vzor populárního výkladu pro ty, co mají panický strach před matematikou, ale spíš se snažím ukázat, že když se chce, dají se věci vyložit přijatelně i pro ty, kteří zrovna např. matematiku nemají v lásce. Takže pro ty, co znají pojem funkce, je zde moje populární povídání o derivaci. Pokud nevíte, co to je, tak právě od toho tohle povídání je. Příklady jsem zvolil tak, aby výklad zvládnul každý zájemce s dobrou znalostí učiva matematiky ze základní školy.
Vlastní povídání
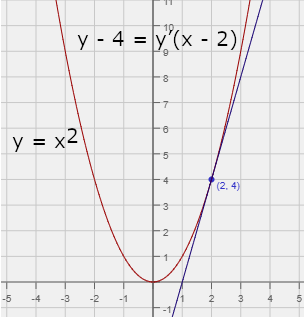
O co půjde, si ukážeme na prvních třech obrázcích; číslo obrázku zjistíte po najetí kurzoru myši na obrázek. Na prvním obrázku vidíme graf funkce y = x2. V bodě (2, 4) je k této křivce nakreslená tečna. Určitě si ještě vzpomenete, jak se správně kreslila sečna ke kružnici v určitém bodě. Stačilo střed kružnice spojit přímkou s daným bodem na kružnici, a pak v tomto bodě vztyčit kolmici k této přímce. Tušíme, že s tečnou k funkci y = x2 to nebude tak jednoduché, protože jaksi nevíme, kde je něco jako střed. Když se ale pozorně podíváme na náš obrázek, možná nás napadne, že pokud budeme znát uhel sevřený s přímkou vedenou bodem (2,4) a rovnoběžnou s osou x máme vyhráno, tečnu snadno nakreslíme. Jak ale zjistit velikost tohoto úhlu? Kdyby nešlo o tečnu ke křivce, ale jenom o samotnou přímku, zjistit zmíněný úhel by nebylo nic těžkého, jak vidět z obrázku č. 2. Stačí určit tangens úhlu, který v kartézské soustavě souřadnic svírá daná přímka (nerovnoběžná s osou y) s kladným směrem osy x. No a z tangens úhlu již lehce určíme pomocí běžné vědecké kalkulačky samotný úhel. Pochopitelně pokud bychom chtěli přímku nakreslit, kromě velikosti úhlu musíme znát i její jeden libovolný bod. A pro připomenutí: Tangens úhlu přímky, který určuje její strmost, se nazývá směrnice přímky, viz obrázek č. 2.
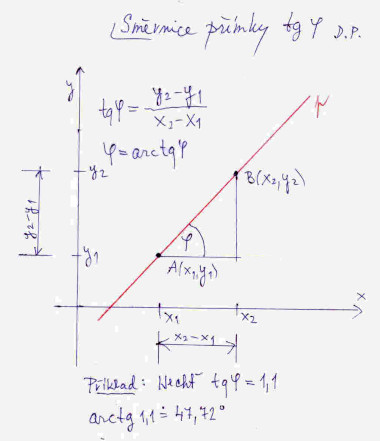
Takže jakže se dopracovat k zmíněnému úhlu v případě křivky? Za chvíli si povíme, že právě tangens námi zmíněného a hledaného úhlu v určitém bodě křivky je právě zmíněná tajemná derivace. Obvykle se značí y’. Na obrázku č. 1 se nám zdá, že v každém bodě funkce y = x2 bychom dokázali tento úhel (zatím nějak) určit, v takovém případě říkáme, že funkce má derivaci. No a když má všude derivaci je také funkce spojitá, tedy taková hezky plynulá bez nějakých divočin, např. jako dráha Formule 1.
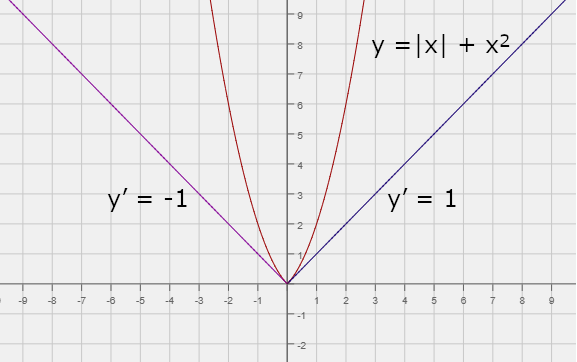
Na obrázku č. 3 vidíme nakreslenou funkci y = |x| + x2. Problém nám tu generuje bod (0,0). Vidíme, že podle toho, zda se k tomuto bodu blížíme zprava (často se značí tohle blížení znaménkem +), nebo zleva (značí se -), tak dostaneme jinou tečnu, jednou je její směrnice +1 a jednou -1. Tuhle funkci asi nebudeme moci považovat za spojitou, přitom, aby to čert vzal, kvůli jednomu jedinému bodu. Takovému problémovému bodu matematici říkají singulární bod křivky, konkrétně tomu našemu bod vratu. To je takový bod, ve kterém existují dokonce dvě tečny křivky, jenomže bohužel rozdílné. Za chvíli si tyhle skutečnosti dokážeme taky matematicky.
Ovšem abychom se k tomu dopracovali musíme si definovat pojem limity. Ono vůbec celý klasický a diferenciální počet stojí na pojmu limity, je to opravdu ten nejfundamentálnější pojem těchto počtů. Intuitivně význam slova limita cítíme, nebudeme se zde ohánět přesnou matematickou definici tohoto pojmu, ale vysvětlíme si tento pojem na dvou jednoduchých příkladech, viz obrázek č. 4. Z obrázku by mělo být jasné, jak se limita v matematice píše. Šípka říká k čemu se proměnná blíží. V příkladě A nemáme žádné problémy s výpočtem limity, x se limitně blíží k 3, tak za proměnnou x dosadíme 3, a limita je vypočtena.
V příkladě B je to složitější, zde se proměnná x blíží k 1, ale do původní definice funkce za x číslo 1 nemůžeme dosadit, neboť z algebry víme, že jmenovatel zlomku nesmí být nula, to proto, že takový výraz nemá rozumný význam. Kupříkladu jaká je hodnota zlomku 5/0? Něčeho 5 kusů mám rozdělit mezi nic lidí ... Kdežto 0/5 už smysl má: nemám nic jablek a mám je rozdělit mezi 5 dětí. Kolik jablek dostane každé dítě? Bohužel žádné, tedy 0. V tabulce jsem naznačil k čemu se blíží hodnota funkce, když se k x blíží k 1 zleva a když zprava. Vidíme že k číslu 2, ale kdybyste se utrápili a do původního výrazu pro funkci dosazovali bližší a bližší hodnoty k 1, nikdy vám numerický výpočet nedá 2. A přesto cítíme, že 2 je limitou dané funkce pro x blížící se k 1. A je to pravda, stačí malá algebraická úprava výrazu, kterým je funkce zadaná a hned je výsledek 2 potvrzen. Tohle když jste pochopili, tak jste pochopili fundament celého klasického diferenciálního a integrálního počtu.

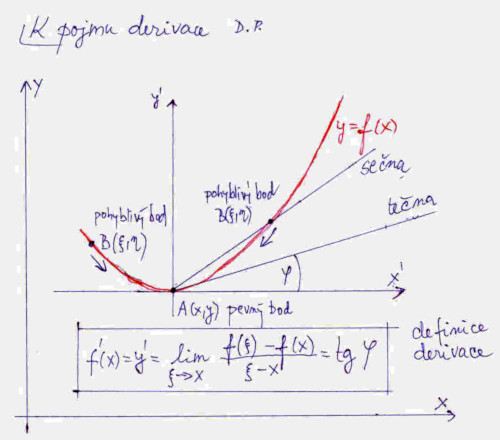
Teď už nám nic nebrání, abychom si definovali názorně derivaci, viz obr. č 5. Vidíme zde křivku a na ní bod B, kterému jsme formálně přiřadili souřadnice z řecké abecedy ξ a η. Jednou si představíme bod B vlevo a jednou vpravo od bodu A(x,y), v němž chceme určit derivaci, tedy směrnici tečny ke křivce v tomto bodě. Bod A je pevný bod, bod B je pohyblivý. Nejprve uvažujme, že je teď napravo od bodu A, a pohybuje se po křivce ve směru šípky k bodu A. Postupně nám body A a B určují řadu sečen, a jak se bod B blíží k bodu A, stejně postupně více a více se zpřesňuje velikost úhlu φ. Až v jakémsi pomyslném okamžiku, kdy bod B splyne s bodem A bude velikost úhlu φ přesně určena. Tedy derivací dané funkce určíme tangens tohoto úhlu; určit velikost úhlu φ je pak již triviální, viz náš příklad výše. Když stejnou úvahu aplikujeme na bod B, který leží od bodu A vlevo, opět dostaneme nějaký úhel φ. Pokud jsou tangenty obou úhlů stejné, říkáme, že v bodě A existuje derivace. Na obrázku č. 3 vidíme, že ne vždy tomu tak musí být. V dolní části obrázku č. 5 pak máme přesnou definici derivace s využitím pojmu limita. V praxi se výpočet derivace pro konkrétní funkce dělá jednodušeji, pomocí určitých pravidel a vzorečků. Tyhle lze nalézt v každé učebnici diferenciálního počtu. V příkladech níže si spočteme derivace dvou funkcí podle naší definice, tedy s využitím limity. Mohu vás ujistit, že hodně vysokoškoláků takhle derivaci ani spočíst neumí, jednoduše pro konkrétní výpočet používají zmíněné vzorečky a zmíněná pravidla. My si ukážeme jak na to pomocí limity. Když to zvládnete, budete malí kingové.
Teď si pomocí limity dokážeme, že derivace funkce y = x2 je 2x, tedy zapsáno dle úzusu y’ = 2x. V našem příkladu na obrázku č. 1 pak bude y’ = 2.2 = 4. Abychom zjistili, jaký úhel odpovídá téhle hodnotě, musíme použít funkci arctg, a zjistíme, že arctg 4 = 75,96°. Což vypadá, že jsme se trefili.
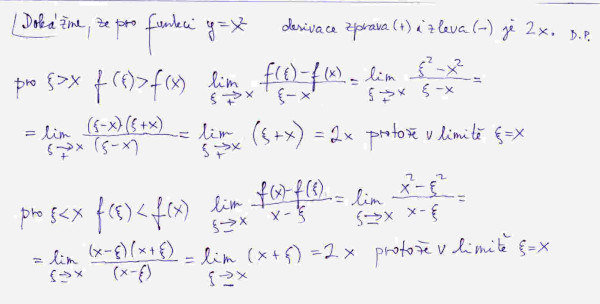
Abych pro představu uvedl alespoň jeden vzoreček pro výpočet derivace, tak derivace funkce y = xn je y’ = nxn-1; kupříkladu pro funkci y = x4 je derivace y’ = 4x3. A vidíme, že tento vzoreček funguje i pro naši funkci y = x2, konkrétně y’ = 2x2-1 = 2x.
A teď kapánek složitější důkaz toho, že funkce y = |x| + x2 v bodě (0,0) nemá derivaci. V tomto případě nám žádný kouzelný vzoreček nepomůže, tady je nutné použít výpočet pomocí limity.
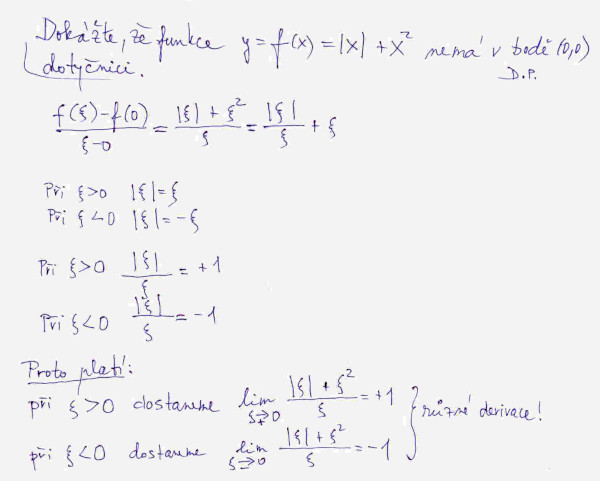
Malý doplněk k směrnici přímky
Díval jsem se do učebnic lineární geometrie, které mám ve své knihovně, ale nikde jsem nenašel důsledně vysvětleno, proč vzorec pro směrnici přímky k = tgφ funguje pro oba případy, tedy pro případ, kdy přímka stoupá, ale i pro případ že klesá. No tak nic, tak jsem to sem dal, viz obrázek č. 8. A tím končím.

V Brně 6. prosince 2024.