Diferenciální rovnice
Dušan Polanský
Začínáme povídáním
Téměř každý obor lidské činnosti je vždy pestřejší a sofistikovanější než se laikovi může na první pohled zdát, tedy kromě politiky, tu může dělat kdokoliv. Nejednou si méně kritičtí jedinci řeknou, že tohle by zvládli levou zadní, jenomže to je většinou jenom zdání, tedy opět kromě politiky. Matematika a vůbec přírodní vědy jsou v tomto jakousi výjimkou, málem tabu, laická veřejnost k ním chová často slepou úctu, u těch nikdo neřekne, tohle je jednoduché, tohle zvládnu. Hlavní důvod bude asi v tom, že zvládnout tyhle obory, chce určité vrozené předpoklady, někdy tomu říkáme talent. Ovšem talent musíte mít, i když chcete být dobrým řidičem, novinářem, kuchařem, zahradníkem, instalatérem, lékařem, konstruktérem, švadlenou apod. Píšu to mimo jiné i proto, že nejsem přítelem žádné glorifikace čehokoliv, jednoduše to chce mít specifické osobnostní předpoklady a ochotu věnovat příslušné činnosti potřebné úsilí a vůli někam to dotáhnout. No a píšu to i proto, že pokud jde o mně, nevím o tom, že bych na něco nějaký talent měl, ale není to žádná tragédie, jsou jistě na světě horší věci. Nakonec každý z nás by určitě chtěl být spíš lemplem, tedy nic pořádného neumět, než trpět nějakou vážnou nemocí.
Onehdy se mi jedna starší dáma, již v důchodu, vysokoškolačka ekonomka, přiznala, že na výšce pro ní byla hotovým utrpením matematika, a že ještě s hrůzou vzpomíná na diferenciální rovnice. Nezdá se mi, že by zrovna na ekonomce diferenciálním rovnicím se věnovala nějaká extra pozornost, ale popravdě ani na technice jsme jim nějak extra moc nedali. Něco ano, ale jenom tak akorát. No a jak se mi ona paní svěřila se svojí nelibostí k diferenciálním rovnicím, uvědomil jsem si, že na svých stránkách vlastně žádné povídání o nich nemám. Tak jsem si řekl, že to musím spravit, třebaže jak úsměvně občas říkám, není nad kvadratickou rovnici. Ale teď k těm diferenciálním. Omlouvám se předem, ale pro porozumění tohoto textu, je potřeba znát elementární základy diferenciálního a integrálního počtu.
Lehký úvod do diferenciálních rovnic

Diferenciální rovnice je taková rovnice, kde neznámá funkce vystupuje v derivaci, může to být první, druhá či vyšší derivace; podle stupně derivace se tomu říká řád diferenciální rovnice. Jinak neznámá funkce v rovnici může vystupovat i bez derivace, ovšem aby to byla diferenciální rovnice, musí tam vystupovat i v derivaci. Ve školské matematice se obvykle neznámá funkce značí y = f(x), aby se zdůraznila její závislost na nezávislé proměnné x. Ve fyzice, chemii, biologii, v ekonomice, technických vědách často nezávislou proměnou je čas, tedy t, pak zápis hledané funkce může vypadat např. nějak takto x = f(t), zde x je pro změnu hledanou funkcí. Ale to jsou jednoduché případy, často mohou být i složitější případy, v jedné rovnici se mohou vyskytovat paralelně derivace podle nějaké proměnné, např. času, a současně derivace podle prostorových souřadnic, a dokonce derivace času a prostorových souřadnic nemusí být stejného řádu. A pak hledaná funkce závisí např. na čase a prostorových souřadnicích. Nemluvě o tzv. počátečních a okrajových podmínkách pro hledanou funkci nebo nezávislé proměnné. Když se podíváte např. do nějaké učebnice fyziky, tak hodně různých zákonitostí je formulována právě diferenciálními rovnicemi. V elektromagnetismu jsou to např. Maxwellovy rovnice, Schrödingerova rovnice v nerelativistické kvantové mechanice, Ilkovičova rovnice v polarografii, vlnová rovnice všude tam, kde se nějaké prostředí vlní atd. Ale to neplatí jenom pro fyziku, ale i pro chemii, biologii, technické vědy. Kam se vzdělaný odborník podívá, všude narazí na diferenciální rovnice. Pokud jde o matematiku, diferenciální rovnice jsou jejím nejrozsáhlejším oborem.
Mým cílem není žádný výklad teorie a praxe diferenciálních rovnic, od toho jsou zde stovky různých matematických knih v různých jazycích o různých stupních obtížnosti, nemluvě o tom, že se učí na všech vysokých technických školách a přírodovědeckých univerzitách. Cílem je lehce naznačit, co to asi ta diferenciální rovnice je, a jak se občas dají bez větších problémů vyřešit. Bohužel pro jejich řešení není k dispozici jeden univerzální postup, spíš je to pestrá plejáda různých méně či více rafinovaných postupů, asi jak to vidíte na úvodním obrázku mé vnučky. Hlava a kousek poprsí dívenky, představuje celý svět diferenciálních rovnic, ale na každou část obrázku byl použitý jiný vzor, což jsou ony zmíněné postupy.
Tři příklady na tři typy diferenciálních rovnic
Rozhodl jsem se pro tři diferenciální rovnice. Proč právě pro tyto tři, to u každé vysvětlím. Klidně to mohli ale být jiné a jiné tři. Typů rovnic je opravdu požehnaně.
Začneme tou první, viz obrázek č. 1 (číslo obrázku se vám objeví po najetí kurzoru myši na obrázek). Tahle diferenciální rovnice je řešitelná, protože umíme provést separaci (oddělení) všech výrazů tak, že důsledně oddělíme výrazy s hledanou funkcí a výrazy s nezávislou proměnnou. Pak stačí už jenom provést integraci. To jenom je trochu zavádějící, někdy příslušný integrál může být pěkně složitý. Ovšem v našem příkladu tomu úmyslně tak není.

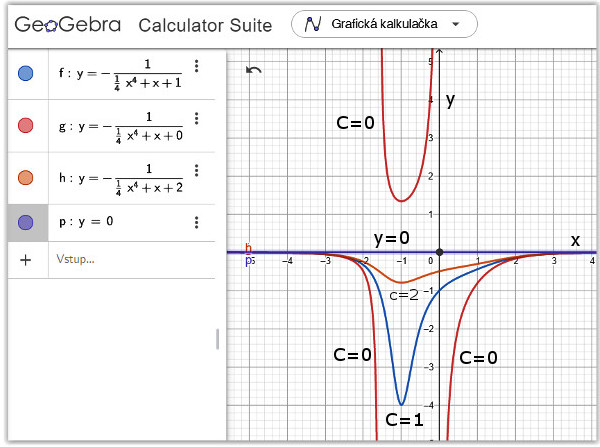
Leč pozorně se podívejme na výsledek, integrační konstanta se v nalezeném řešení vyskytuje ve jmenovali. Různou volbou konstanty C dostaneme výrazně rozdílná řešení, jak můžete vidět na obrázku č. 2. A ještě jedno malé překvapení. Při separaci proměnných jsme předpokládali, že y ≠ 0. Ale když 0 dosadíte do původní rovnice pak 0 řešení vyhovuje, tedy i y = 0 je řešením! Jenom doplním, že k zobrazení řešení rovnic jsem použil výborný free produkt GeoGebra.
Druhá rovnice, kterou budeme řešit je druhého řádu, tedy neznámá funkce se vyskytuje v řešené rovnici v druhé derivaci. Tahle rovnice se dá řešit substituci p = dy/dx, tím dosáhneme toho, že z druhé derivace dostaneme derivaci první, tedy dp/dx. No a na tu pak použijeme postup z první rovnice. Je otázkou, které rovnice se takto dají řešit. Pro větší názornost jsem vypsal jejich seznam, viz obrázek č. . My budeme fíkaně řešit jenom tu nejjednodušší, ostatní jsou detailně popsané v každé učebnici o diferenciálních rovnicích. Námi řešená rovnice je ta, na kterou narazí každý student, který má v prvním semestru fyziku. Tam se vysvětluje, že dx/dt je rychlost a že d2x/dt2 je zrychlení. A úloha spočívá v tom, vyřešit rovnici d2x/dt2 = a, kde a je konstantní zrychlení, a navíc jsou zadány počáteční podmínky. Řešení by mělo být zřejmé z obrázku č. 3.

Otázkou je, jaké typy rovnic se dají řešit zmíněnou substitucí, tedy p = dy/dx? Několik příkladů jsem uvedl na obrázku č. 4.
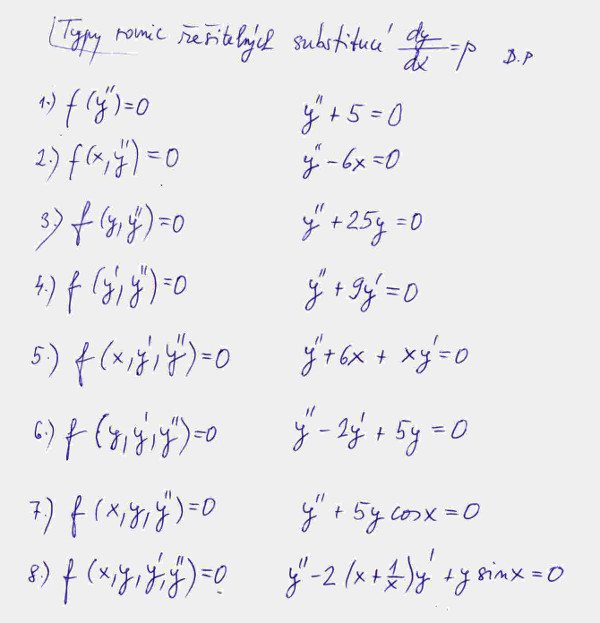
Třetí rovnice ukazuje, to co jsem napsal již výše, že na řešení diferenciálních rovnic se používají různé speciální postupy. Jeden takový postup je ukázán u tzv. homogenní rovnice. Ta se vyznačuje tím, že dokážeme na jednu stranu dostat dy/dx, a na druhou stranu výraz obsahující hledanou funkci a nezávisle proměnnou ve tvaru y/x. Pokud se to povede, lze na řešení aplikovat postup na obrázku č. 5.

Vše si ukážeme na praktickém příkladu, viz obr. č. 6.

Ve výsledku se nám zákonitě objevila nějaká konstanta, zde C’, abychom jí dali konkrétní hodnotu zvolíme např. x = 1 a y = 1. Pak nám vyjde C’ = 4.
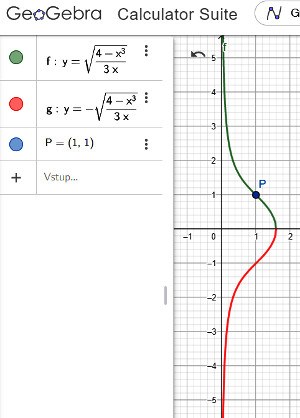
Malá zrada spočívá v tom, že když si vykreslíme graf výsledné funkce s touto hodnotou konstanty C’, tak vidíme, že funkce y(x) je nejednoznačná, protože např. pro x = 1 dostaneme dvě hodnoty y, jedna je +1 a druhá −1. Vše vidíme na obrázku č. 7. Ovšem jak se někdy říká, že někdy je vše jenom otázkou úhlu pohledu. Když si graf otočíte o 90° doleva, tak role y a x se vymění, x se stane závislou na proměnné y, tedy x = f(y), a pak již řešení lze považovat za jednoznačné. A v tom spočívá homogennost této rovnice, x i y vystupují v obou rolích.
Takový trik se vám nepovede např. u kružnice. Nechť její rovnice v implicitním tvaru je x2 + y2 = r2, kde r > 0. Tuto křivku lze vyjádřit jako graf dvou funkcí. V horní polorovině, kde y > 0, jako y = sqrt (r2 − x2), a vdolní polorovině, kde y < 0, jako y = − sqrt (r2 − x2). V bodech (−r, o) a (r, 0) oba grafy splývají. Sqrt značí druhou odmocninu, viz např. Excel.
Něco malého závěrem
Snad tento malý výlet někoho z čtenářů inspiroval k tomu, aby se o svět diferenciálních rovnic začal zajímat. Jak jsem již ale napsal, tento svět je velice rozsáhlý, a navíc je zbytečné se trápit řešením rovnic, které se ve vaší konkrétní odborné praxi nevyskytují. Znáte to, škola je škola, a praxe je praxe. Přiznám se, že v mé odborné praxi jsem na diferenciální rovnice přímo nesetkal, když nepočítám to, že jsem studentům coby učitel ukazoval, jak se dá na počítači najít numerické řešení některých diferenciálních rovnic. Ale to bylo tak dávno, že to už ani pravda není, a navíc to nebyla praxe, ale jenom škola.
V Brně 15. května 2023.