Odvození velikosti dostředivé síly
Dušan Polanský
Docela dobře si pamatuji, jak většina z nás, já nebyl výjimkou, na základní či střední škole (na stavební průmyslovce byla fyzika pouze první rok) pracovala při řešení příkladů z fyziky. Myšlenkový postup byl jednoduchý. Kterýpak vzoreček napasovat na hodnoty, které se objevily v zadání? O nějaké fyzikální úvaze předcházející vlastnímu řešení nemohla být ani řeč. Osobně jsem se natrénoval na jakés takés fyzikální myšlení a interpretace vzorců až později sám. Ne, že bych to pro život potřeboval, o tom nemůže být ani řeči, ale znáte to, není nad to zatěžovat si hlavu zbytečnostmi, třebaže chápu, že kdyby si např. takto zatěžovali hlavu všichni ti, co dali vale partnerovi, to by svět nemohl fungovat, jelikož by zde bylo více neurotiků než těch normálních.
Či už tak nebo onak jeden vzoreček mi byl vždy obzvláště sympatický. Je to vzoreček pro velikost odstředivé síly při pohybu po kružnici. Učí se již na základní škole. Není moc složitý, zde je jeho nejpoužívanější tvar: fod = mv2/r. Síla dostředivá má stejnou velikost jenom má opačný směr, což je docela logické. Z pohledu matematického se jedná o relativně jednoduchý vzoreček, ovšem z pohledu fyzika je obsahově docela bohatý. Vidíme, že velikost jedné nebo druhé síly je především determinována rychlostí, jelikož závisí od čtverce rychlosti. Na tohle je dobré pamatovat hlavně při jízdě v zatáčce např. autem, protože i při na první pohled zdánlivě bezpečné rychlosti se nám může stát, že se dočkáme překvapení v podobě vyjetí z jízdní dráhy a přistání v příkopu nebo v lepším případě na svodidlech. Kupříkladu při rychlosti 30 km/hod, čtverec rychlosti dává hodnotu 900, ale při rychlosti 50 km/hod již 2500, což je významný nárůst hodnoty vystupující ve vzorečku pro odstředivé zrychlení, přitom samotná rychlost se až tak významně nezvýšila. Nemluvě o tom, že u takového plně naloženého náklaďáků i hmotnost je významným příspěvkem k velikosti odstředivé síly. Také nesmíme zapomenout, že rovněž závisí na poloměru, velikosti síly ubývá s velikostí poloměru, naopak síly přibývá se zmenšováním poloměru. Znalec dopravního stavitelství namítne, že na silnici se pro zajištění plynulého přechodu z přímého úseku do oblouku používá speciální křivka, obecně jí říkáme přechodnice. V ČR se u silnic jako přechodnice používá klotoida, a u té se poloměr křivosti mění plynule, obecně je v každém bodě jiný, ovšem tenhle detail nebudeme při našem jednoduchém výpočtu zohledňovat, protože konkrétní poloměr klotoidy v určitém místě přechodnice lze zjistit např. z podrobných tabulek. Síla odstředivá nám ale i pomáhá, kupříkladu u odstředivek se využívá odstředivého efektu pro ždímání již vypraného mokrého prádla.
Užitečným motivačním příkladem pro vysvětlení působení obou sil je otáčení těžšího předmětu uvázaného na provázku; také kdo by to v životě alespoň jednou nezkusil. Při otáčení (jedná se o rovnoměrný nezrychlený pohyb po kružnici) jasně cítíme, že provázek musíme pevně držet a neustále přitahovat k sobě, neboť jinak hrozí ulítnutí předmětu z dráhy otáčení a nedej bože, kdyby někdo stál poblíž a předmět by jej trefil. Pokud je provázek slabý a odstředivá síla veliká, hrozí, že provázek se přetrhne a předmět odletí do prostoru. Tohle jsou již jenom z osobní zkušenosti lehce pochopitelné skutečnosti, proto ani kvůli jim tohle povídání nepíšu. Půjde nám o to, ukázat, že vzoreček pro dostředivou sílu lze odvodit relativně jednoduše a není potřeba sahat k sofistikovaným nástrojům, jako je např. diferenciální počet; v učenějších knihách fyziky se tak děje. Pochopitelně náš důkaz z titulu přibližnosti nebude zcela dokonalý, ale snad bude o to více názorný, nakonec daleko více se soustředíme na fyziku než na matematiku, třebaže bez ní bychom se k výsledku nedopracovali. Co k tomu budeme potřebovat je uvedeno na obrázku č. 1, vlastní odvození je uvedeno na obrázku č. 2.
Nejdříve, co k našemu odvození velikosti dostředivé síly budeme potřebovat. Především z dynamiky druhý Newtonův pohybový zákon, jehož matematické vyjádření F = ma známe všichni. Z mechaniky jednoduchý, ale elegantní důsledek vzorečku pro výpočet vzdálenosti, kterou urazí za určitý čas bod při rovnoměrném zrychleném pohybu, viz č. 1. Když do obecného vzorečku pro vzdálenost dosadíme za t = 1, tedy chceme znát překonanou dráhu za časovou jednotku, dostaneme vztah a = 2s. Malý příklad na aplikaci tohoto vztahu. Gravitační zrychlení na Zemi je 9,81 ms-2. Ze vztahu a = 2s plyne, že volně padající předmět k zemi urazí za jednu sekundu přibližně 4, 9 m. Využijeme i vzoreček pro výpočet dráhy v případě rovnoměrného pohybu s = vt, protože náš předmět se bude po kružnici pohybovat rovnoměrně. Z klasické geometrie budeme potřebovat Euklidovu větu o odvěsnách, viz č. 2, a Thaletovu větu o obvodových úhlech nad průměrem, viz č. 3. Odvození těchto vět lze nalézt v každé učebnici Euklidovské geometrie. Ovšem nám stačí pochopení obsahu těchto vět, jejich odvození pro nás není stěžejní.

Konečně se můžeme pustit do odvozování vztahu pro dostředivou sílu při rovnoměrném nezrychleném pohybu po kružnici. Pro názornost, se vrátíme k našemu příkladu s otáčením předmětu uvázaným na provázku. Výchozí situaci vidíme na obrázku č. 2. Předpokládejme, že náš předmět ve výchozím stavu se nachází v bodě T. Jenom pro úplnost dodejme, že vektor rychlosti v každém bodě kružnice je tečnou ke kružnici. Za časovou jednotku se předmět přesune do bodu A. Oblouk TA jsme nahradili tětivou TA. Je si dobré uvědomit, že tento malý švindl není až tak neoprávněný. Časová jednotka nemusí být zrovna 1 sekunda, ale klidně 1 miliontina sekundy, pak lze předpokládat, že v naší úvaze rozdíl mezi obloukem a tětivou bude velice malý. Z toho také plyne, že v našem přiblížení délka tětivy TA je současně i rychlostí pohybu, jelikož je to dráha vykonaná za jednu časovou jednotku.
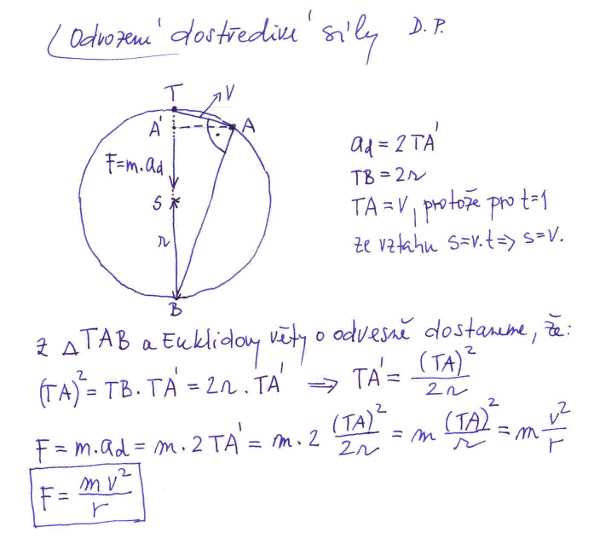
Sice je hezké, že náš předmět se pohybuje rovnoměrným nezrychleným pohybem, ale aby tomu tak mohlo být, musí zde působit centrální dostředivá síla. Podobně je to s naší matičkou Zemí, kdyby Slunce na naši Zemi nepůsobilo centrální dostředivou silou, tak bychom tu určitě nebyli. Jak víme, tahle síla podle Isaaca Newtona je F = mad. Hmotnost předmětu známe, ale jaké je ad, tedy dostředivé zrychlení? Na obrázku č. 1 jsme si ukázali, že pro rovnoměrně zrychlený pohyb platí vztah a = 2s. Jenomže jakou vzdálenost s dosadit za dráhu? Z pohledu dostředivé síly je to dráha TA’, kde A’ je projekce bodu A na průměr TB. Teď už jde jenom o to, jak šikovně vyjádřit tuto dráhu. Určitě bude záviset na poloměru kružnice r a poloze bodu A, tedy na rychlosti bodu po kružnici. Výpočet TA’ vidíte na obrázku č. 2. Výpočet F = mad je už pak zcela triviální.
Naše odvození je, jak jsme si již uvedli, trochu nedůsledné, ale nepostrádá atributy fyzikálního myšlení. Fyzikální interpretace našeho vzorečku není až tak složitá, ovšem finální vzorce ve fyzice jsou nejednou složitější než náš vzoreček, nemluvě o tom, že často v nich vystupují kromě skalárů a vektorů složitější matematické objekty, jako jsou např. tenzory, spinory, grupy. Dokonce se najdou i vzorce, které smysluplné fyzikální interpretaci zatím úspěšně odvolávají. Ovšem vždy by mělo platit, že řešení příkladu z fyziky začíná fyzikální úvahou. Pokud bude správná, napasovat ten správný vzoreček a dosadit do něj správné hodnoty za jednotlivé veličiny by již neměl být až takový problém. A to je pro tentokrát vše.
V Brně 24. května 2017.