Eulerovo číslo e
Dušan Polanský
Matematika se stává více a více abstraktní vědou. Tento vývoj je motivován snahou zobecnit dosažené speciální poznatky. Každé zobecnění jaksi automaticky generuje větší formalizaci matematického zápisu. Nakonec proč ne, alespoň se ušetří papír a koho by bavilo vypisovat dlouhé vzorce či výpočty. Problém je tu jediný, silně formalizovaným zápisům rozumí jenom matematici. Ale nakonec to platí pro každý vědný obor, v matematice to cítíme o něco více proto, že je to předmět školou povinný. Ovšem myslet si, že vystačíme jenom s abstraktními pojmy a formálními zápisy je iluzorní. Praxe je vždy konkrétní. Nejen ta životní, ale i matematická. Výsledek musí být obvykle hmatatelný, uchopitelný, jinak je dost těžko v běžné lidské praxi využitelný. Většina teoretických matematiků namítne, že někdy je dost těžké vysvětlit nám laikům abstraktní pojmy v názorných a uchopitelných pojmech. Osobně si myslím, že je to spíš o schopnosti či neschopnosti věci srozumitelně a jasně vyložit, což ne každý umí. Pochopitelně to neplatí jenom pro matematiku. Srozumitelných vykladačů je holt málo. Správný výkladač musí vidět pořádně pod povrch daného problému či jevu a ne jenom psát životopisy matematiků či historii důkazů. Za knihy napsané v podobném stylu doporučuji peníze nevyhazovat.
Ale nechme obecného povídání a kritiky matematiků či jiných odborníků a zkusme si jenom tak pro radost či jenom z nudy konkrétně započítat, pokud možno bez abstrakce a přílišné formalizace. Počtářská praxe se pro většinu z nás nejčastěji hodí k výpočtům procent a finančním kalkulacím. Jenomže to jsou dost nudné výpočty, nakonec je umí každý kalkulátor či tabulkový procesor. Dumal jsem, na čem by se dalo demonstrovat kouzlo ne zcela jednoduchých výpočtů. Nakonec jsem se rozhodl pro výpočet Eulerova čísla pomocí binomické věty.
Pro ty, jimž se dále uvedený výpočet bude zdát příliš složitý, jsem v dodatku popsal jiný způsob výpočtu Eulerova čísla. Abych je ušetřil mechanického počítání, tak jsem doplnil postup, jak veškerý výpočet lze provést tabulkovým procesorem Excel.
Binomickou větu by šlo zde odvodit, ale tím by text zbytečně nabobtnal. Nakonec binomická věta se probírá na střední škole. Doufám, že pán učitel či paní učitelka vám tuhle větu nenapsali na tabuli bez odvození, což by bylo možné označit z jejich strany za barbarství. V každém případě budeme předpokládat, že ji známe, ale pro pohodlí čtenáře jsme na obrázcích číslo 1. a 2. (číslo obrázku se vám zobrazí po najetí kurzoru myši na obrázek) provedli jakousi rekapitulaci této věty a jejího použití pro výpočet mocnin binomů. O binomické větě mluvíme proto, že binom má dva členy a binomická věta nám říká, jak bez dlouhého počítání lze najít libovolnou mocninu binomu neboli dvojčlenu. Na obrázku číslo 2. vidíte známý Pascalův trojúhelník a pod jeho čísly v řádcích je uvedeno jeho praktické použití právě pro výpočet mocnin binomu. Jenom si připomeňme, že jednotlivá čísla v tomto trojúhelníku dostaneme sečtením dvou čísel nad číslem, které chceme spočíst. Druhé pravidlo stanoví, že po obou stranách, které začínají u vrcholu s číslem 1, jsou všude jedničky.


O Eulerovém čísle, píše se jako malé e, si ještě nakonec textu něco učeného řekneme, ale nejdříve si spočteme jeho přibližnou velikost. Proč jenom přibližnou si vysvětlíme na konci našeho povídání. K výpočtu budeme potřebovat právě zmíněnou binomickou větu. Tahle věta je docela důležitá, jelikož bez ní by nebylo ani tzv. vysoké matematiky.
Podívejme se spolu na obrázek č. 3. Binomickou větu jsme aplikovali na binom (1 + b). Poté jsme do výsledku, je to jakási dlouhá řada, dosadili za b = x/n, přičemž n je přirozené číslo a x libovolné číslo. Opět nám vyšla jakási dlouhá řada, z které jsme vypustili zakroužkované členy. Proč právě je? Představme si, že číslo n budeme neustále zvyšovat. Vidíme, že v naší řadě se číslo n vyskytuje pouze ve jmenovateli zakroužkovaných členů. Dokonce jsou tam jeho mocniny nebo se číslo n násobí dalšími celými čísly. Takové zlomky při vzrůstajícím n se budou jistě blížit nule, což nás laicky „oprávňuje“ takové členy zanedbat. A nakonec nám z celé řady zbydou pouze členy uvedené v posledním řádku. Jenomže pokud n se blíží nekonečnu, těchto členů i tak bude nakonec nekonečně moc. Nemluvě o tom, že jsme nekonečný počet jich zakroužkovali. Ale nekonečno již takové je, má v sobě další a další nekonečna, dokonce nekonečný počet nekonečen. Kdyby tomu tak nebylo, nebylo by to nekonečno.

Malé x je libovolné číslo. Dosaďme za něj 1. Abychom si zápis řady ještě více zjednodušili, použili jsme k zápisu členů řady faktoriál. Vše je uvedeno na obrázku č. 4. Teď již nám nezbývá nic jiného, než vzít kalkulačku a počítat. Výpočet je proveden s přesností na 7 desetinných míst. Přesnější výsledek na 10 desetinných míst je uveden v dolním řádku. Určitě vás napadne přirozená otázka, zda lze Eulerovo číslo zapsat přesně. Ne nelze, dokázal to v roce 1737 Leonhard Euler. Číslům s takovou vlastností říkáme čísla iracionální, taková čísla nelze vyjádřit přesným zlomkem. Kupříkladu 8/5 je přesně 1,6. Zlomek 7/3 je již jiný, nevyjadřuje přesné číslo, třebaže jej umíme přesně zapsat: 2,3333... Víme, že do nekonečna můžeme psát za desetinnou čárkou číslici 3. Pro e přesný zlomek neznáme a nikdy znát nebudeme. Přibližný zlomek pro e je např. 87/32 nebo ještě přesnější 878/323. Zda má nějakou periodu opakování, jako v případě zlomku 7/3, kde je periodou číslice 3, také nevíme. Na Internetu si můžete najít jeho zápis na stovky a stovky desetinných míst, ale na žádnou logiku číslic za desetinnou čárkou zatím nikdo nepřišel. Navíc číslo má další zajímavou vlastnost. Eulerovo číslo je transcendentní. To znamená, že není kořenem žádné algebraické rovnice, takovou rovnicí je např. kvadratická rovnice. Transcendentnost e dokázal v roce 1873 Charles Hermite.

Velikost čísla e lze odvodit i jinými postupy, ale náš postup je snad nejjednodušší. Jinak číslo e možná znáte z přirozených algoritmů, vyskytuje se i v mnohých vzorcích fyziky, pravděpodobnosti, statistiky a jiných oborů, obvykle kde je potřeba vyjádřit růst nějaké veličiny. Je to takový malý konkurent slavného Ludolfova čísla pí, což je rovněž číslo iracionální a transcendentní.
Dodatek Jak jsem slíbil výše, ukážeme si i jiný způsobe výpočtu Eulerova čísla. Motivací nám bude naše finanční chamtivost. Máme 1 Kč a je zde banka, která nám nabizí roční úrok 100 % a přitom se neplatí žádná daň ze zisku. Je nám jasné, že po roce budeme mít 2 Kč. To je docela dobrý kšeft, jenomže naše chamtivost nezná mezí, chceme naši těžce vydělanou 1 Kč uložit ještě lépe. Banka nám proto nabídne úrok 50%, přičemž úrokovací období je půl roku. Spočteme si z hlavy, kolik budeme mít v bance peněz na konci roku. Za první půlrok nám banka připíše 0,50 Kč, takže v pololetí budeme mít 1,50 Kč. Ale ještě není konec roku, takže 1,50 Kč leží stále v bance. Na konci roku nám banka připíše 0,75 Kč, což je polovina z 1,50 Kč. Na konci roku máme tedy v bance 2,25 Kč. Jenomže ani to nám nestačí. Když se nám banku podaří přesvědčit, aby sumární roční úrok byl 100 %, ale úrok se připisoval častěji, tak z naší 1 Kč vyzískáme pěkný balík. Banka souhlasí a nabídne nám úročení po čtvrt roce při úroku 25 %. Po kapánek delším výpočtu, ale jinak zcela triviálním, zjistíme, že na konci roku budeme mít v bance přibližně 2,441 Kč. Banka bude nakonec tak velkorysá, že si můžeme zvolit sami dobu připisování úroku. Dobře. Ať se tedy úrok připisuje každý týden, pak každou hodinu, pak každou sekundu, pak třeba každou půlsekundu atd. Asi již tušíte, kam směřujeme. Ano. Na konci roku naše výsledná hodnota v bance nikdy nepřekročí hodnotu Eulerova čísla e.
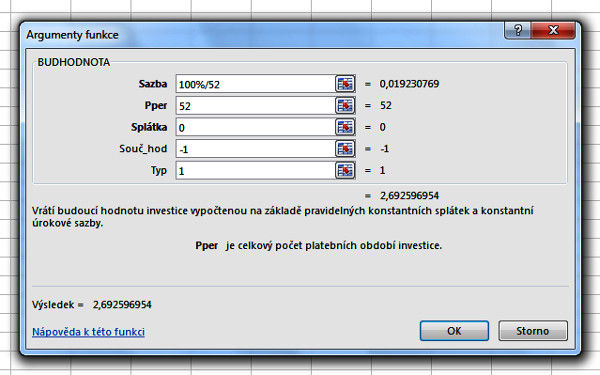
Přesvědčme se o tom. Abychom se z výpočtů nezbláznili, použijeme tabulkový procesor Excel a jeho finanční funkci BUDHODNOTA. Pro názornost a pochopení zadávání parametrů jsem naskenoval vstupní okno pro zadání parametrů této funkce. Vidíme, že pokud se úrok bude připisovat každý týden (100%/52), na konci roku budeme mít v bance přibližně 2, 692 Kč. Zkuste si spočíst několik dalších výsledných hodnot. Kupříkladu pro připisování každý den zadáte do prvního pole 100%/365, do druhého pole 365, ostatní pole ponechte podle obrázku. Zkuste zvýšit frekvenci připisování na hodiny, minuty, sekundy. Uvidíte, že nikdy nepřekročíte hodnotu Eulerova čísla e. Není to zajímavé? A to je již vše.
V Brně 13. září 2016.