Fermatův princip
Dušan Polanský
Proč jsem si k povídání vybral Fermatův princip? Důvody jsou tři. První je osobní, jsou mi sympatické obecné, málem filozofické principy, z nichž lze logickou cestou odvodit vysoce specializované výsledky. Druhý důvod souvisí úzce s prvním, po principu virtuálních prací a konstantní rychlosti světla je mi to nejsympatičtější princip. Třetí je pragmatický, díval jsem se do několika učebnic fyziky a nikde nebylo uvedeno odvození zákonu lomu, na němž budeme použití Fermatova principu demonstrovat, i s detailně vypočteným příkladem, který by ukázal, jak se musí ve fyzice při počítání myslet. Pro zájemce uveďme, že ve fyzice pro technické školy od Z. Horáka a F. Kupku (např. SNTL a ALFA v roce 1976) je zákon lomu odvozen - velice elegantně - z Fermatova principu s využitím virtuálních (myšlených) posuvů. Doporučuji místo koukání do televize k pozornému přečtení. Sice v životě to nikdy nebudete potřebovat, jedině pokud studujete, tak na zkoušce, ale člověk je tvor metafyzický, a proto rád dumá o zbytečnostech. Tak proč ne také o virtuálních posunech. I Bůh je pro mnohé bytost virtuální a přitom o něm přemýšlejí.
Náš postup důkazu bude ale jiný. Pokud jde o znalosti potřebné k pochopení našeho povídání, vystačíme se středoškolskou matematikou, ale pokud pojem derivace a operace derivování jsou vám cizí, musíte uvěřit tomu, co bude kolem toho řečeno. Ovšem znalost derivování není nezbytná pro pochopení výkladu. Konec konců Pierre de Fermat žil v letech 1601 až 1665 a v té době se diferenciální a integrální počet teprve rodil.
Fermat svůj princip formuloval obecně: Světlo šíří v prostoru z jednoho bodu do druhého po takové dráze, že doba potřebná k překonání této dráhy má extrémní hodnotu. Často se uvádí, že má minimální hodnotu, ale obecně tomu nemusí vždy tak být. S použitím tohoto principu lze vystavět celou geometrickou optiku. Pomocí Fermatova principu si odvodíme zákon lomu, který známe již ze základní školy. Pochopitelně tam nám zákon byl sdělen jako holý fakt bez jakéhokoliv logického zdůvodnění a vysvětlení jeho krásy a hloubky. Nevím jak na vás, ale na mne působil dost fádně.
Na prvním obrázku je zadání příkladu. Z bodu A (je ve vzduchu) vyšleme světelný paprsek a chceme zjistit, jakou trasu si paprsek zvolí, aby bod C (je ve vodě) dosáhl za extrémní dobu. Zatím ještě nevíme, zda to bude minimální nebo maximální doba. Bod A je nad hladinou moře a jednotek, bod B je pod vodou b jednotek. Vodorovná vzdálenost bodů A a C je c jednotek. Rychlost světla ve vzduchu je v, ve vodě w.
Zkusme uvažovat jako paprsek světla. Asi by od něj nebylo moc chytré, kdyby si zvolil trasu APC. Rychlost světla ve vodě je totiž menší než ve vzduchu, takže na časově nejkratší času to nevypadá, jelikož dlouho bude putovat pod vodou. Trasa AQC vypadá velice nadějně, dokonce při prvním pohledu by si člověk, ne paprsek, myslel, že to bude trasa, která bude časově nejkratší, jelikož rychlost světla ve vzduchu je větší než ve vodě. Tahle trasa má malý háček, paprsek musí dorazit vzduchem až do bodu Q a pak úsek b absolvovat pod vodou. Paprsek je ale chytrý, ví, že někdy může být výhodnější neputovat až do bodu Q, ale již v bodě B se ponořit do vody, čímž si ušetří kousek času, který by potřeboval k dosažení bodu Q a třebaže teď trasa pod vodou bude delší než úsek QC, přece jenom sumárně na čase ušetří. Na našem příkladu uvidíme, zda se nemýlí.
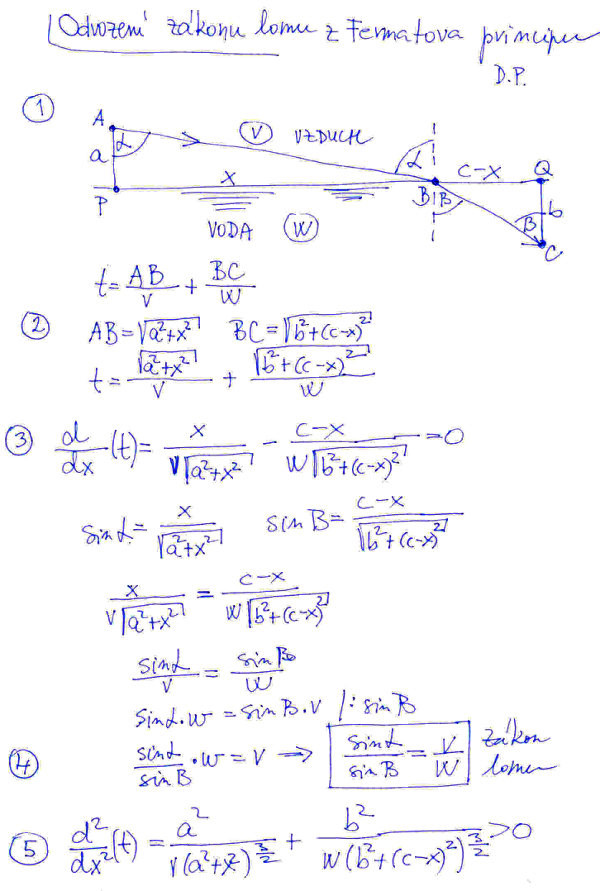
V bodě č. 2 je uveden obecný výraz pro výpočet času t potřebného na překonání vzdálenosti ABC. Pro sestavení vzorečku pro výpočet času t jsme vystačili s Pythagorovou větou. Abychom spočetli vzdálenost x, tedy polohu bodu B využijeme jednu ze základních vět diferenciálního počtu. Ta praví, že pokud je funkce spojitá a derivovatelná na intervalu I a nabývá-li maxima nebo minima v určitém bodě intervalu I, tak první derivace v tomto bodě je rovna nule. Graficky si derivaci funkce f(x) můžeme představit jako směrnici funkce f(x), což je obecně nějaký graf. Tedy derivace je tangenta úhlu, který svírá tečna ke křivce f(x) v určitém bodě s kladným směrem ody x. Pokud je derivace kladná, křivka vyjádřená funkcí f(x) je rostoucí, pokud záporná, tak klesající. Pokud v určitém bodě má mít funkce minimum nebo maximum, musí křivka změnit směr. No a v bodě kde se tak stane, je derivace nulová, to znamená, že tečna ke křivce f(x) svírá s osou x nulový úhel. Výsledek výpočtu první derivace je uveden v bodě č. 3. Pokud vás zajímá podrobný výpočet, ten je uveden v příloze č. 1. Pod výpočtem derivace jsou uvedeny vztahy pro výpočet sin (alfa) a sin (beta) – budou se nám za chvíli hodit –, které jsme si lehce odvodili z obrázku v bodě č. 1. Po jednoduchých úpravách jsme se v bodě č. 4. dopracovali k zákonu lomu, který známe již ze základní školy.
Ovšem k našemu dalšímu cíli, výpočtu polohy bodu B jsme se zatím nedopracovali. Je přirozené si dokonce položit otázku, zda bod B opravdu leží mezi body P a Q. Vidíme, že první i druhá derivace jsou definovány pro všecka x, tedy nejen pro interval P až Q, takže teoreticky by bod B mohl ležet mimo interval P až Q. Znáte to, jsou lidi, kteří nechtějí kupovat levné věci, ale drahé, jelikož jsou obvykle kvalitnější. Kdoví jak myslí paprsek, možná si chce cestování užít. Z diferenciálního počtu víme, že pokud druhá derivace je v celém intervalu kladná, první derivace je v tomtéž intervalu funkce rostoucí od mínus nekonečna do plus nekonečna a může se nejvýš jednou rovnat nule. Když si dosadíme do první derivaci, viz bod č. 3, x = 0, vyjde nám záporný výsledek. Pro x = c vyjde kladný výsledek. Tím máme jistotu, že rovnice uvedená v bodě č. 3 má jediný kořen právě mezi body P a Q.
O tom, zda se jedná v daném bodě o maximum nebo minimum, rozhoduje druhá derivace. Pokud je větší než nula, tak je to minimum, pokud menší než nula, tak maximum. Výsledek výpočtu druhé derivace je uveden v bodě č. 5. Podrobný výpočet druhé derivace je uveden opět v příloze č. 1. Druhá derivace je od mímus nekonečna do plus nekonečna větší než nula, což znamená, že světelný paprsek bude hledat trasu, kterou urazí za minimum času. Výsledek je ve shodě s Fermatovým principem.
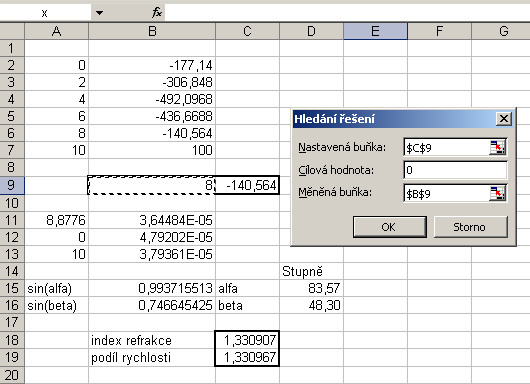
Teď konkrétní příklad. Jeho zadání je uvedeno na obrázku č. 2 v bodě č. 1. Je to stejný příklad, jako byl uveden na obrázku č. 1 pouze s tím rozdílem, že v našem zadání jsou uvedeny konkrétní hodnoty. V bodě č. 2 jsme se dopracovali k rovnici pro výpočet vzdálenosti bodu B od bodu P. Teď stojíme před problémem vyřešit tuhle rovnici. K tomu využijeme např. tabulkový procesor Excel. Popis řešení je uveden v příloze č. 2. Kritická vzdálenost x nám vyšla přibližně 8, 8786. V bodě č. 4 jsou spočteny doby, za které světelný paprsek urazí tři trasy. Vidíme, že trasa ABC je opravdu nejkratší. V bodě 5 jsme si ověřili pomocí zákonu lomu, zda jsme spočetli x správně. Vypadá to, že ano, jelikož poměr sinů i rychlostí nám dává stejnou hodnotu 1.3309. A to je vlastně vše. Jak prosté a krásné.

Příloha číslo 1.

Příloha číslo 2.
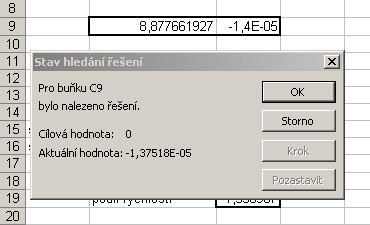
Jak lze vyřešit v Excelu rovnici uvedenou na obrázku č. 2 v bodě č. 3? Excel má k tomu šikovný nástroj Hledání řešení. Malá komplikace je v tom, že chce, abychom jako vstupní parametr zadali přibližnou hodnotu hledaného kořene. V našem příkladu to není až takový problém. Víme, že kritický bod x musí ležet v intervalu 0 až 10 km. Zadáme si výpočet levé strany rovnice, polynomu, v několika bodech, my jsme zvolili body 0, 2, 4, 6, 8 a 10. Vidíme, že v bodě 8 je hodnota polynomu záporná, kdežto v bodě 10 již kladná. To znamená, že kořen musí ležet v intervalu 8 až 10, tam někde bude protínat vodorovnou osu. V Hledání řešení... (V Excelu 2013 Nástroje >> Hledání řešení...) jsme zadali přibližnou hodnotu kořene 8. Po 100 iteracích, tento počet (lze jej změnit) je nastaven v kartě Výpočet v Možnosti..., jsme se dopracovali k hodnotě 8,8776. Jaké hodnoty se zadávají do vstupních polí dialogového okna Hledání řešení, je zřejmé z prvního obrázku. Buňku B9 si doporučuji pojmenovat x, aby analogie se zadáním byla úplná. V buňce C9 je vzorec pro výpočet levé strany rovnice, v němž neznámou máme pojmenovanou jako x. Výsledek výpočtu je vidět na dalším obrázku. K čisté nule jsme se nedopracovali, což je dáno počtem iterací, a tím, že kořen je pravděpodobně iracionální číslo. Ovšem dosažená přesnost je více než dostačující.
V Brně 11. listopadu 2014.