Statistiky ve fyzice
Dušan Polanský
Většinu střípků píšu náhodně, obvykle mě inspiruje konkrétní událost, zážitek či jenom dílčí postřeh. Podobně tomu je v tomto případě. V červnu jsem si vzal den dovolené, abych v Malackách vyřídil nějaké věci po odchodu mladšího brášku Vlaďa na věčnost. Autem nejezdím, takže vlak. Na Hlavním nádraží v Brně jsem byl včas, do odjezdu vlaku zbývalo ještě něco přes půl hodiny; přesněji, myslel jsem si, že zbývá. Bezcílně jsem bloumal budovou nádraží a přitom bloumání jsem potkal jednoho známého. Je filatelistou jako já, a tak jsme si chvíli povídali o známkách. Poté jsem loudavě odkráčel na první nástupiště. Málem mě ale trefilo! Na prvním nástupišti jsem se již jenom mohl podívat na poslední vůz odjíždějícího vlaku směrem na Břeclav. V hlavě jsem si posunul odjez o 10 minut později! Co teď? Nic. Počkat na další spoj, který má odjezd přesně za dvě hodiny.
Jelikož čekat dvě hodiny v nádražní hale či vysedávat v restauraci je otrava, vyrazil jsem se projít do centra Brna, beztak tam chodím velice málo. Mimo jiné jsem se zastavil v knihkupectví Academie na Náměstí Svobody. Nebyl jsem tam již rok či dva, ale teď jsem potřeboval zabít čas a hlavně zklidnit svoji naštvanost na vlastní blbost. V poličce se zlevněnými tituly jsem si všimnul knihy autorů Miroslava Brdičky a Viktora Trkala ml.: Profesor Viktor Trkal, s podnadpisem Pouť moderní fyzikou. Kniha vyšla v Academii v Praze 2007. O koho jde, jsem dobře věděl, jelikož kdysi jsem vlastnil jeho kvalitní knihu Mechanika hmotných bodů a tuhého tělesa (NČSAV, 1956). Komusi jsem ji pak prodal; ten kdosi málem brečel, že ji nutně potřebuje k psaní doktorandské práce. Knihy totiž po nedobrých zkušenostech nepůjčuji, jednoduše ji zájemci prodám. Když si ji lakomec koupit nechce, má smůlu. Vlastně je ještě třetí možnost, knihy, o nichž vím, že je nestihnu již přečíst (čtu kvůli zraku již minimálně) a zdají se mi zcela běžné, dám do veliké papírové krabice a tu postavím k popelnicím. Vždy se rozeberou. Knihu z roku 2007 jsem si nakonec koupil ani ne tak kvůli fyzice, jako spíš velice zajímavé obrazové příloze, v níž jsou kromě jiného k vidění i pohlednice s pozdravy od matematika prof. Václava Hlavatého a básníka Petra Bezruče. Mé filatelistické srdíčko obrázky pohlednic potěšily. Mít je tak ve sbírce, to by bylo! Ty bych nikdy neprodal! Proto se nedivte, že ve vlaku jsem si v první řadě prohlédl obrazovou přílohu.
Text knihy jsem jenom zběžně prolistoval. Ale výjimka vždy potvrzuje pravidlo. Na straně 79 a kousku strany 80 jsem se začetl soustředěně. Profesor Viktor Trkal zde v příspěvku nazvaném Padesát let kvantové fyziky, předneseném v roce 1950, vysvětluje na základě jednoduchého podobenství, pocházejícího původně od Erwina Schrödingera (1887–1961), rozdíl mezi třemi statistikami používanými či nepoužívanými v kvantové fyzice. Přiznám se, že nejsa fyzik, kvantové fyzice jsem se nikdy nevěnoval. To, co znám, nestojí za řeč. Tři zmíněné statistiky jsem pochopitelně podle názvů znal a něco málo o nich i věděl, ale při čtení ve vlaku jsem si z krátkého textu zcela jasno v nich neudělal. Nic, při cestě zpět do Brna si musím vše nakreslit! A jak se můžete přesvědčit, cosi jsem ve vlaku nakreslil.
Po dlouhém prologu, jak je již mým nedobrým zvykem, si pointu statistik mikrosvěta podle podobenství Erwina Schrödingera, ač jeho původní text neznám, vysvětlíme. Ničeho se nebojte, vystačíte se selským rozumem a vše si vysvětlíme na příkladech mimo fyziku. Znění mého textu je pochopitelně inspirováno i textem na stranách 79 a 80 výše zmíněného titulu.
Fyzika mikrosvěta má jeden veliký problém. Základních částic (tenhle pojem berte relativně, časem může být mnohé jiné, jako že již i bylo) je docela dost a ne všechny se chovají stejně. Chování těch kterých částic je popsáno mimo jiné příslušnou statistikou. Statistika není nic jiného jenom přesně definovaná pravidla chování pro určitý typ částic. Dnešní kvantová fyzika uvažuje tři typy statistik, přičemž jeden typ je čistě teoreticky, podle něj se počet stavů (viz dále), v nichž se částice mohou nacházet, nepočítá, ale pro pochopení pravidel platných pro tu kterou statistiku je tento případ důležitý z teoretického hlediska.
Jak již bylo řečeno, vše si vysvětlíme na třech příkladech mimo fyziku. Částice si budeme představovat jako ceny udělené žákům a jedno konkrétní udělení cen žákům bude představovat jeden konkrétní stav, v němž se částice mohou nacházet. Je určitě rozdíl, zda cena je udělena tomu, nebo onomu žákovi. Dále budeme znát konkrétní pravidla pro udělení cen a budeme chtít spočíst počet možností pro jejich udělení. Žáci budou tři: Toník, Vojta a Jindra. Ceny nebudou pokaždé stejné a budou mít dokonce i různá pravidla pro jejich udělení. Tyhle pravidla jsou vlastně pravidla té které statistiky. Terminologii tohoto odstavce si musíme dobře pamatovat, protože jsou zcela zásadní pro pochopení dalšího výkladu. Při jeho čtení doporučuji sledovat příslušný fragment obrázku.
Klasická Maxwell–Boltzmannova statistika. Touhle statistikou se žádné základní částice mikrosvěta neřídí, ale pro pochopení širšího kontextu si ji vysvětlíme. Dvě ceny, které mají být uděleny, jsou dvě různé medaile. Jedné budeme říkat Černá, druhé Bílá. Zásadní je, že medaile (tedy částice) jsou jedna od druhé rozpoznatelné! Jistě tušíte, proč se tahle statistika nehodí pro mikrosvět. Identifikovat každou částici by byla docela pěkná fuška, když si uvědomíme, že základních částic určitého typu v jakémkoliv kousku nějaké hmoty je nepředstavitelně obrovský počet. Pravidla této statistiky jsou velkorysá. Medaile mohou být uděleny jednak dvěma různým žákům, jednak obě medaile může obdržet za vynikající výkon i jeden jediný žák. Kolik je možností udělení dvou různých medailí našim třem žákům? Možností je devět, viz obrázek. Tedy je celkem devět možných stavů, v nichž se částice mohou nacházet. Z pohledu učitele je devět možností, jak žáky ocenit. Jak to nakonec v dnešní době dopadne, závisí na hodnocení paní učitelky. A určitě nejeden z nás bývalých žáků ví ze svých zkušeností, že hodnocení ne vždy musí být objektivní.
Je nabíledni otázka, zda lze počet stavů ověřit výpočtem. Jistě, vzorečkem S = zc, kde z = počet žáků a c = počet rozpoznatelných cen. V našem příkladu S = 32 = 9.
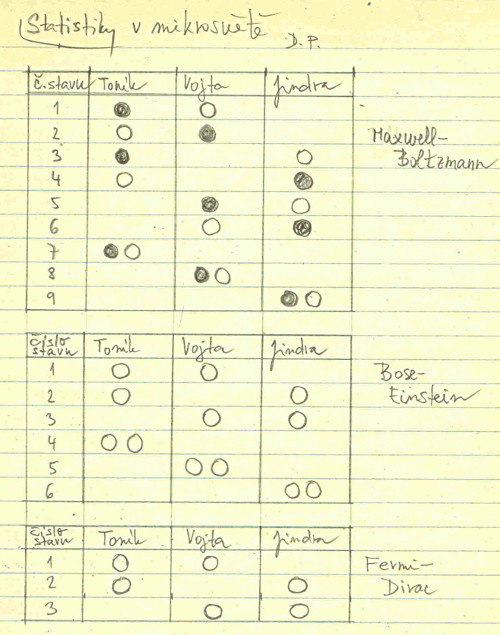
Bose–Einsteinova statistika.Medaile jsou sice opět dvě, jenomže jsou nerozpoznatelné! To je již situace, kterou si dovedeme v mikrosvětě představit. Medaile mohou být uděleny jednak dvěma různým žákům, jednak obě medaile může obdržet za vynikající výkon i jeden jediný žák. Možností rozdělení medailí v tomto případě je celkem 6, opět viz obrázek. Tedy z pohledu částic fungujících podle této statistiky je celkem 6 možných stavů, v nichž se dvě nerozpoznatelné částice mohou nacházet.
A opět je zde otázka, zda lze počet stavů ověřit výpočtem. Ano: S = (z + c - 1)!/(c!(z-1)!), kde z = počet žáků a c = počet nerozpoznatelných cen. V našem příkladu S = (3 + 2 - 1)!/(2!(3-1)!) = 6.
Fermi–Diracova statistika. Medaile jsou opět dvě a opět jsou nerozpoznatelné! Medaile mohou být uděleny dvěma různým žákům, ale obě medaile nesmí obdržet jeden jediný žák! Za těchto podmínek jsou pouze 3 možnosti, kterými mohou být rozděleny medaile, viz obrázek. Z pohledu částic fungujících podle této statistiky jsou pouze 3 možné stavy, v nichž se dvě částice mohou nacházet.
A opět vzoreček pro výpočet počtu stavů: S = z!/(c!(z-c)!), kde z = počet žáků a c = počet nerozpoznatelných cen. V našem příkladu S = 3!/(2!(3-2)!) = 3.
Teď opustíme žáky a medaile a podíváme se na částice. Budou nám stačit dvě a budeme předpokládat, že každá částice může být ve dvou různých stavech: první stav, druhý stav. A částice budeme umísťovat do krabic, přičemž v jedné krabici může být pouze jedna částice. Jaké případy mohou nastat podle zmíněných statistik?
V Maxwell–Boltzmannově statistice jsou částice navzájem rozpoznatelné, takže mohou nastat tyto 4 případy: 1. dvě částice jsou v prvním stavu, 2. dvě částice jsou v druhém stavu, 3. první částice je v prvním stavu a druhá v druhém stavu, 4. první částice je v druhém stavu a druhá v prvním stavu.
V Bose–Einsteinově statistice jsou částice navzájem nerozpoznatelné, takže mohou nastat tyto 3 případy: 1. dvě částice jsou v prvním stavu, 2. dvě částice jsou v druhém stavu, 3. jedna z částic je v prvním stavu a druhá v druhém stavu.
Ve Fermi–Diracově statistice jsou částice navzájem nerozpoznatelné a navíc se bere v úvahu ještě Pauliův princip, podle něhož v jednom stavu může být pouze jedna jediná částice, proto může nastat pouze jeden případ: jedna z částic je v prvním stavu a druhá v druhém stavu.
Co s tím dále fyzika přesněji fyzici? Z výše uvedených principů se pro každou statistiku odvodí (dost pracně) tzv. distribuční (rozdělovací) funkce: fMB(E), fBE(E), fFD(E). Tyto funkce udávají střední počet částic ve stavu s energií E pro tu kterou statistiku. Tenhle údaj je totiž pro pochopení fungování mikrosvěta velice důležitý. Pokud vám to zní příliš učeně, představte si, že máte takovou funkci pro zjištění počtu občanů, jejichž majetek dosahuje určité výše; tedy hodnota majetku je analogem energie E. Kupříkladu zadáte hodnotu 36 milionů a funkce vám vychrlí počet občanů ČR, kteří vlastní majetek v uvedené výši. Pochopitelně je nelogické pracovat s přesnou hodnotou majetku, spíš nás bude zajímat určité rozpětí majetku, tedy kolik občanů má majetek kupříkladu v rozpětí 31 až 36 milionů. Ale pokud známe distribuční funkci rozdělení majetku, k téhle hodnotě se dokážeme bez problému dopočítat.
Jaké částice se kterou statistikou řídí neboli jakou mají rozdělovací funkci? Maxwell–Boltzmannovou například molekuly, tedy např. plyn všude kolem nás. Bose–Einsteinovou tzv. bosony. Bosony mají celočíselný spin (0, 1, 2, ...), což je jakýsi vnitřní moment částice; velice přibližně si jej lze představit (fyzikové nás za toto zjednodušení nepochválí) jako otáčející se káču. Touhle statistikou se řídí i fotony, což jsou základní částice světla. Fermi–Diracova statistikou zase tzv. fermiony, které mají poločíselný spin (1/2, 3/2, ...). Takovou částicí je např. elektron. Fermiony podléhající Pauliho vylučovacímu principu, který aplikovaný např. na elektronový obal atomu tvrdí, že v konkrétním kvantovém stavu popsaném určitými kvantovými čísly může být nejvýše jeden elektron. Vidíme, že není náhoda, že při našem vysvětlování této statistiky žák nemohl obdržet dvě medaile, jelikož tím bychom porušili Pauliho vylučovací princip. U Bose–Einsteinovy statistiky jeden žák dvě stejné medaile obdržet mohl. A u Maxwell–Boltzmannovy statistiky je povoleno vše, nejsou žádná omezení. Je vidět, že molekuly si mohou dělat, co chtějí. Ty se mají!
Dočetli jste elementární text z fyziky mikrosvěta. Pokud vás nebaví vysedávat v hospodě nebo u televize, kupte si nějakou jakž takž srozumitelnou knihu o kvantové fyzice a začtěte se. Sice k ničemu vám to v životě nebude, ale to stejné lze říct např. o televizi či dlouhém vysedávání v hospodě. A to je konec krátkého povídání o statistikách v mikrosvětě způsobené jedním zmeškaným vlakem. Co vám budu povídat, já měl na sebe takový vztek ...
V Brně 29. listopadu 2016.