Geometrická řada neboli záliba trochu jinak
Dušan Polanský
Matematika je jedna z mých zálib. Tedy ne stále, ale občas ano. Také si nepředstavujte, že když nemám co dělat nebo na mne sedne splín, začnu zuřivě počítat matematické příklady či řešit rébusy apod. Je to většinou věc nálady, náhody nebo objevení problému, který mě zaujme a když cítím, že mám šanci se dopracovat v rozumném čase výsledku. Záliba je něco, co nás baví, u čehož dokážeme zapomenout na starosti, trápení, smutek nebo jenom zahnat nudu. To, že máme v něčem zálibu, neznamená, že danou zálibu musíme perfektně zvládat nebo jí zcela rozumět. Kupříkladu jsou sportovní fanoušci, kteří v životě sport, jemuž fandí, nikdy nedělali. Jsou vášniví čtenáři, kteří v životě nikomu nenapsali ani vícestránkový dopis, natož povídku nebo něco podobného. Jsou lidé, co milují muziku a přitom nikdy nehráli na žádný hudební nástroj. Já jsem podobný milovník matematiky, nikdy jsem neuvažoval matematiku dělat profesionálně, neboť na to jednoduše nemám. Dokonce v mládí jsem si matematiku, kvůli učitelům na základní a střední škole, na několik let doslova zhnusil. Postupný obrat nastal až na vysoké škole, kde jsem začal postupně objevovat její krásu a přirozenou logičnost, tentokráte pro jistotu již bez učitelů. Podobně jako v dnešním matematickém střípku.
Někdy před Vánocemi jsem jenom tak bloumal po německých internetových stránkách. Důvod je prostý: německy trochu umím a mám rád německou romantickou literaturu. No a při tom mém googlování jsem zcela náhodou ve veliké množině obrázků uviděl i jeden, který, jak jsem vytušil, bude mít něco s matematikou. Bylo tomu tak. Byl to barevný obrázek, na němž bylo bez vysvětlení konstatováno, že se lze k součtu nekonečné konvergentní geometrické řady (tj. že její součet je konečné číslo) dopracovat i pomocí geometrického názoru. Základní návod obrázek dával, ale výpočet zcela chyběl. Problém mě zaujal, leč zpočátku jsem se vůbec nechytal. Ale kdybych se chytal, asi by mě problém nezaujal. A tak jsem si musel zopakovat geometrickou řadu, trochu se potrápit, než jsem konečně výpočet zdolal. Pokud máte zájem, dále je vše vysvětleno.
Na prvním obrázku – v rámci jakési přípravy na výpočet součtu nekonečné sestupné geometrické řady pomocí geometrického názoru – je moji rukou naškrábána malá rekapitulace učiva o geometrických řadách ze střední školy. Vzoreček pro součet sn konečné geometrické řady nedokazuji, neboť jej lze nalézt v každé učebnici matematiky pro střední školy. Rekapitulace je osvěžena dvěma příklady. Na prvním je ukázáno, že v případě, že počet členů geometrické řady je veliký a kvocient q geometrické řady je menší než 1 nebo -1, lze někdy i intuitivně odhadnout součet nekonečné geometrické řady. Po tomto příkladě je uvedeno klasické odvození pro výpočet součtu nekonečné geometrické sestupné řady, tj. řady, u níž kvocient q je v absolutní hodnotě menší než 1. Další příklad ukazuje jednoduchou aplikaci tohoto vzorečku. Je ukázáno, že nekonečný periodický zlomek lze převést na pravý zlomek.

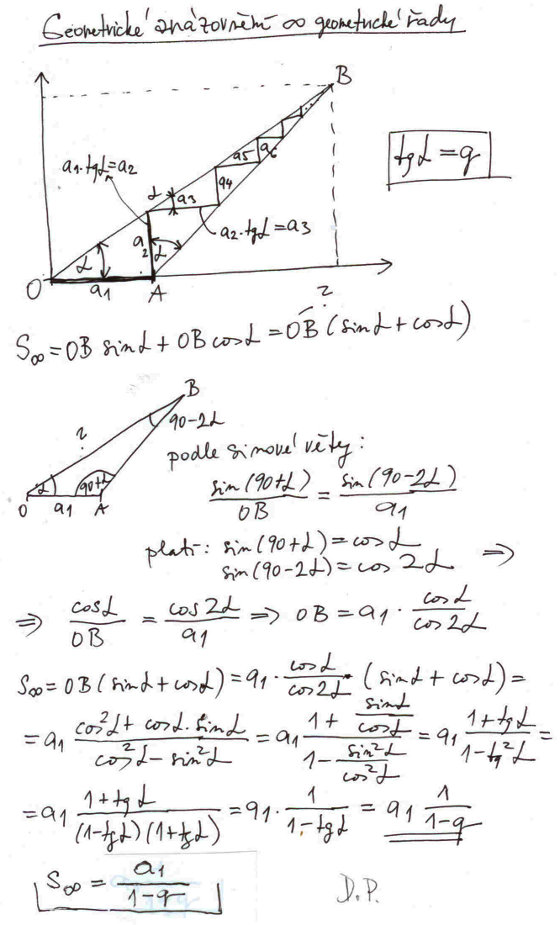
No a na druhém obrázku je ukázáno a dokázáno, jak lze pomocí geometrického názoru odvodit vzoreček pro výpočet nekonečné geometrické konvergentní řady. Naservíroval jsem vám vše, nic jsem neutajil, ale pro jistotu přidávám vysvětlení postupu kreslení obrázku. Nejdřív pod úhlem alfa, kde tangens alfa se rovná kvocientu q, vyneseme přímku ve směru 0B, souřadnice bodu B zatím neznáme. Na horizontálu naneseme úsečku o velikosti prvního člena geometrické řady, tj. a1. Z bodu A opět pod úhlem alfa, tentokrát úhel měříme od vertikály, vyneseme přímku AB. Výpočet a konstruování dalších členů geometrické řady je snad již zřejmý. Vidíme, že součet geometrické řady tvoří součet celé lomené čáry, jejíž dílčí úsečky jsou členy geometrické posloupnosti. A také je vidět, že součet celé řady je tvořen součtem průmětů čáry 0B na horizontální a vertikální osu. Abychom pokročili dále, musíme nějak spočíst délku úsečky 0B. K tomu jsme využili sinovou větu, opět viz každou učebnici matematiky pro střední školy. Další výpočet je již jenom rutinní záležitostí. V každém případě jsme se dopracovali ke stejnému výsledku jako na předchozím obrázku. Matematik by asi ještě dodal, že je potřeba dokázat, že přímky 0B a AB se protnou v bodě B. Budiž. Protnou se proto, že chceme aby tg alfa byl menší než jedna (podmínka konvergence řady), tj. úhel alfa musí být menší než 45°. Když se podíváte na pomocný obrázek vysvětlující použití sinové věty, je zřejmé, že pokud úhel alfa bude menší než 45°, máme co do činění opravdu s trojúhelníkem.
Na matematice je hezké, že téměř vše lze vyjádřit či vysvětlit i geometricky. Tedy pokud dotyčnému problému člověk opravdu rozumí. Snad tenhle jednoduchý příklad vám ukázal nebo alespoň přiblížil krásu onoho propojení klasického výpočtu a geometrie.
V Brně v den Svatí tři králové Léta páně 2013.