Holičství a těžší rovnice o jedné neznámé
Dušan Polanský
Život sám je často o řešení rovnice o mnoha neznámých. A bohužel často je tahle rovnice velice těžce řešitelná, proto raději nechme život životem a vyrazme do školy a to konkrétně na hodinu matematiky na základku. Tam se učí i rovnice o jedné neznámé. Jinak tomu nebylo ani za nás když já chodil na devítiletku v letech 1958 až 1967. Pokud si vzpomínám dokonce jsme v devítce brali soustavu dvou rovnic o dvou neznámých, ale to je již s ohledem na můj věk látka příliš složitá, raději zůstaňme u jedné neznámé, protože starší člověk nemá přepínat ani fyzické síly, ani mysl.
Nejprve si vyřešíme relativně jednoduchý příklad na jednu neznámou, a to dvěma různými způsoby: klasickým způsobem, jak se to běžně učí ve škole, a pak za pomoci grafu. No a abychom se také naučili něčemu novému, náš příklad zobecníme. Ono to totiž v exaktních vědách tak již chodí, snahou je najít obecnější řešení, které zahrnuje v sobě různé speciální případy. I my takové obecnější řešení najdeme a uvidíme, zda náš speciální příklad lze vyřešit dosazením konkrétních hodnot do obecného řešení. Při hledání obecného řešení narazíme na součet geometrické posloupnosti, ale žádné obavy, těm, kterým to nic neříká, ukážeme, jak se takový součet poměrně lehce spočte. Takže dost z úvodů a jdeme na zadání našeho příkladu, tedy zatím toho speciálního.
Chlápek provozuje tradiční pánské holičství, což znamená, že se chodí k němu stříhat a holit pouze osoby mužského pohlaví. Je mu trapné vybírat peníze od zákazníků přímo, tak jde na to různými oklikami. Jednou u něj byli tři zákazníci a povídá: Pánové, podívejte se tam na ten stolek. Jak vidíte, má zásuvku, a v té je nějaká částka. Každý z vás se po ostřihání do zásuvky podívá a zjistí, jaká částka v zásuvce je, poté dá do zásuvky stejnou částku a vezme si 40 Kč. Bohužel tentokráte mu jeho populistický kalkul moc nevyšel, když zákazníky ostříhal a podíval se do zásuvky, nebyla tam ani koruna. Kolik korun bylo v zásuvce na začátku?
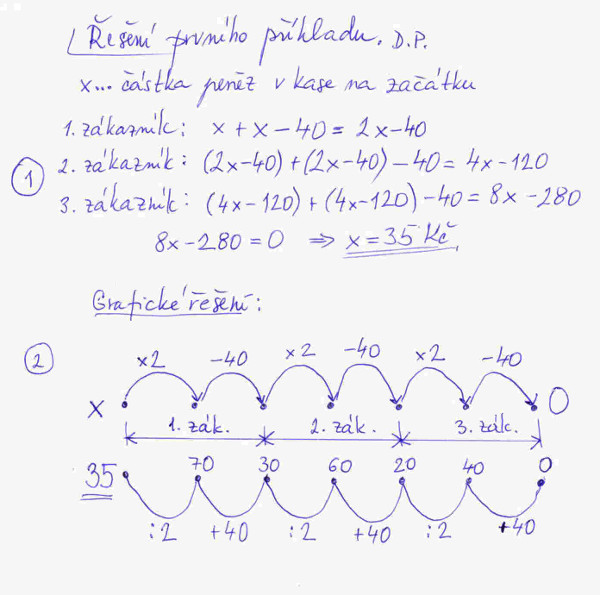
Řešení je na obrázku č. 1; číslo obrázku zjistíte po najetí kurzoru myši na obrázek. Myslím, že obě řešení nepotřebují zvláštní výklad. Pouze u grafického řešení si dovolím nenápadně zmínit, že při postupu vpřed, počáteční částku sice neznáme, ale víme, jaké aritmetické operace tři zákazníci postupně vykonávají, a rovněž víme, že na konci nebyly v zásuvce žádné peníze. Při zpětném postupu známé výchozí hodnotu, tedy 0 Kč, a jaké inverzní operace vůči těm původním při postupu vpřed, musíme postupně provést, abychom se dopracovali k částce, která byla v zásuvce na počátku. Proč inverzní operace? Má to jednoduchou logiku zřejmou z dvou jednoduchých příkladů. Dám vám 100 Kč, tím budete mít to, co jste měl na začátku + 100 Kč. Jakou částku jste měl, než jsem vám peníze dal? Jednoduše odečtu 100 Kč od částky, kterou máte po mém velkorysém daru, nebo mi vrátíte 100 Kč a já se podívám, kolik vám zbylo. Prostě jednou +, pak –, tedy inverzně. Podobně je to s násobením a dělením. Někdo vám dá tři krát tolik korun, kolik máte. Vy mi prozradíte, kolik máte teď, a ptáte se, kolik jste měl na začátku. Řešení je prosté, vydělím finální částku třemi.
A teď slíbené zobecnění našeho příkladu. Jediná změna bude, že holičství nahradíme bankou a zákazníky klienty. Doporučuji pozorně sledovat analogii obecného zadání se zadáním příkladu s holičstvím.
V bance je na začátku x Kč. Do banky přijde postupně n klientů. První klient vloží do banky takovou částku, že množství peněz v trezoru se zvětší q1krát. Z banky si odnese p1 Kč. Druhý klient vloží do banky takovou částku, že množství peněz v bance se zvětší q2 krát. Z banky si odnese p2 Kč. Ntý klient vloží do banky takovou částku, že množství peněz v bance se zvětší qn krát a z banky si odnese pn Kč. Nakonec v bance zůstane a Kč. Kolik korun v bance bylo na začátku?
Jak na to půjdeme? Mohli bychom postupovat jako při řešení prvního příkladu klasickým postupem, tedy ne grafem, ale popravdě vykouzlit z tohoto postupu obecné řešení by nebylo vůbec jednoduché. Ale zkusit to můžete. My si ale raději pomůžeme malou fintou. Přepíšeme si tři zápisy pro naše tři zákazníky do jedné jediné rovnice. Jak? To vidíte na obrázku č. 2 pod bodem č.1. Z tohoto jednořádkového zápisu již relativně snadno odvodíme obecnější zápis, který vyhovuje našemu obecnému zadání. Tento zápis, včetně řešení této zdánlivě složité rovnice, vidíte v bodě č. 2. V bodě č. 3 je speciální řešení této rovnice, kdy násobky jsou stejné, rovněž i částky, které si klienti z banky odnesou. A dle našeho příkladu z holičství, v bance zůstane trezor prázdný, což je sci-fi, jelikož pokud zůstane prázdný, to znamená, že banka byla vytunelovaná. V každém případě se nás složitý vzorec výrazně za těchto podmínek zjednoduší, ale aby se tak stalo, musíme vědět, jak spočíst součet geometrické posloupnosti, viz dodatek. Jenom si připomeňme, že pokud v geometrické posloupnosti vydělíte kterýkoliv člen členem, který mu bezprostředně předchází, vždy dostaneme stejnou konstantu, této konstantě se říká kvocient. Aby byla geometrická posloupnost jednoznačně definovaná, kromě kvocientu ještě musíme znát první člen a počet členů posloupnosti. Pokud je počet členů nekonečný, mluvíme o řadě. Občas se to plete.

Abychom si ověřili, že náš vzorec opravdu funguje, dosadili jsem do něj hodnoty z příkladu v holičství. Výsledek nám vyšel stejný. Vidíme, že příklad z holičství jsme nakonec vyřešili třemi postupy. A o tom také občas matematika je. A to je vše.
V Brně 10. června 2020.
Dodatek. Výpočet součtu geometrické posloupnosti o n členech.
