Integrál je krásná věc
Dušan Polanský
Populárních knih o matematice vychází v poslední době málem požehnaně. Jenomže jsou obvykle až tak populární, že jsou málem k ničemu. Utápí se v historických detailech, obecném povídání a konkrétním výpočtům se vyhýbají, že prý běžný čtenář, laik, by jim beztak neporozuměl. Mám pocit, že je to jenom výmluva. Komerční popularizátoři látku, o níž píší, buď nemají do hloubky zvládnutou, a proto ji také neumí srozumitelně a jasně vyložit, nebo ji zvládnutou mají, ale také ve finále neumí to, co ti první.
Nejsa výjimkou v umění popularizace, nejsa matematik a nemaje látku, o níž budu vykládat, ani zdaleka do hloubky zvládnutou, chtěl bych se těm, kteří neví, co to integrál je, kouzlo téhle nádherné matematické operace pokusit přiblížit. Znalosti předpokládám, jako obvykle, na úrovni první třídy střední školy. Tam, kde budu pracovat i se znalostmi nad tento rozsah, pokusím se vše srozumitelně buď vysvětlit, nebo šikovně obejít; přesně jako v životě.
Vše na světě má svůj protipól, negaci, výjimkou nejsou ani matematické operace. Sčítání má odčítání, násobení dělení, no a integrál derivaci. Sice operace derivování je v matematice veledůležitá, ale my se jí raději rafinovaně vyhneme. Integrál si vysvětlíme na výpočtu ploch ohraničených osou x a shora nějakou křivkou y = f(x). Není to náhoda, jelikož právě výpočet obsahu plochy složitých plošných útvarů motivoval matematiky k zavedení integrálu. Integrální počet někdo využívá i v praxi; tím nemyslím učitele, co jej učí nebo jej používají při výkladu jiné látky, jelikož škola není praxe. V mém profesním životě tomu tak nebylo, vždy jsem vystačil se čtyřmi základními aritmetickými operacemi na úrovni základní školy, takže integrál je pro mne především krásná věc, asi jako když se dívám na hezkou ženu ve středním věku.
Než se po úvodu dlouhém jak nohy dívky Miss Universe – volí se od mého roku narození – konečně podíváme na první obrázek, tak ještě jedno malé uklidnění: nemějte obavy z počátečních obecných úvah, v dalším již budeme konkrétní. Na obrázku označeném A vidíme symboliku integrálu a jeho geometrický význam. Symbolem integrálu je fajfka. Tahle fajfka nám pomůže elegantně spočíst velikost plochy pod křivkou danou rovnicí y = f(x). Dolní a bočné ohraničení plošného obrazce je zřejmé z obrázku. Křivka může být jakákoliv, např. horní polovina kružnice, elipsy, či jenom přímka. Nebojte se podivného symbolu dx, je to diferenciál x, čteme déx. Ten nám říká, že integračním intervalem je osa x. Integrační interval uvedený na dolním a horním konci znaku integrálu nám říká, odkud pokud na ose x integrujeme. Na našem obrázku od souřadnice a po souřadnici b. Pokud dokážeme funkci y = f(x) integrovat, výsledek integrace si označíme obecně F(x), pak stačí do F(x) dosadit horní hranici integračního intervalu x = b a odečíst ji od F(x), kde za x jsme dosadili spodní hranici integračního intervalu, tj. x = a. Vypočtený rozdíl je hledaný obsah plochy. Funkce F(x) se nazývá primitivní funkce. Pokud vynásobíme plochu nějakým číslem c, tak jsme neudělali nic jiného, než příslušně zvětšili či zmenšili plochu o c násobek, proto číslo c můžeme vyjmout před znak integrálu, formální zápis téhle skutečnosti můžete rovněž vidět na obrázku.
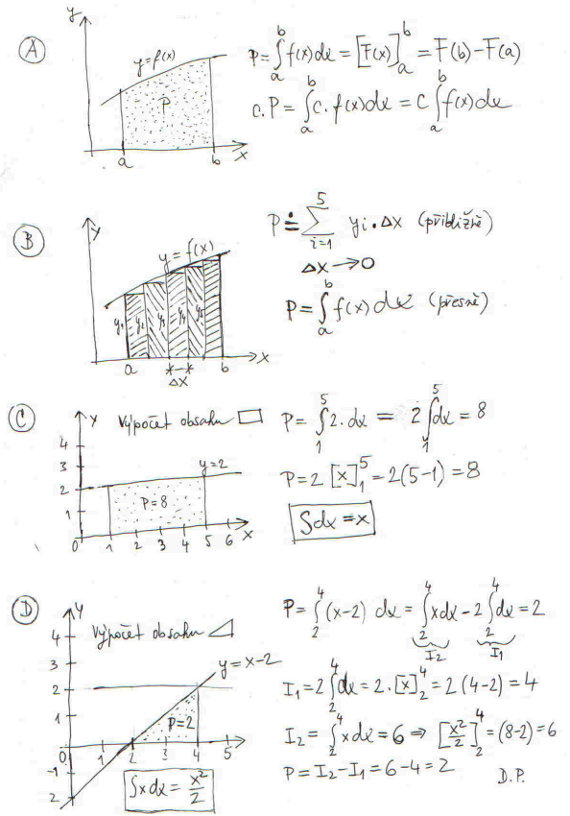
Jak spočíst alespoň přibližně obsah jakékoliv plochy? Obrázek B nám říká, jak na to. Osu x si rozdělíme na malinkaté pravidelné dílky, nad každým dílkem si vztyčíme obdélníček, jehož horní strana je rovnoběžná s osou x, čímž se jenom přibližně (křivka je obecně křivá, obdélník je rovný) blíží svoji délkou délce příslušného fragmentu křivky f(x). Již z obrázku lze odhadnout, že když plochu těchhle přibližných obdélníčků sečteme, tak jejich suma se bude blížit hledanému obsahu plochy pod křivkou y = f(x). Čím bude dělení osy x hustější a hustější, tím se naše suma obdélníčků bude blížit skutečnému obsahu plochy přesněji a přesněji. Jenomže i když budou intervaly dělení super malinkaté, stále nebudeme znát naprosto přesný obsah hledané plochy, tedy s jedinou výjimkou, když křivka bude úsečka rovnoběžná s osou x, v tom případě suma uzounkých obdélníčků přesně dá obsah plochy, tedy obdélníka. No a právě integrál je tu od toho, aby nám ušetřil dřinu s počítáním. Pokud umíme integrál z funkce f(x) spočíst, tedy známe funkci F(x) máme vyhráno; dokážeme vypočíst přesný obsah plochy pod křivkou y = f(x).
Obecné je k ničemu, s tím si vystačí tak politici nebo lidé, co jim padlo do klína bez sebemenší námahy veliké bohatství. Když integrálem lze spočítat obsah plochy, musí výpočet o to více fungovat i na obyčejný obdélník. Výpočet plochy obdélníka integrálem je znázorněn pod písmenem C. Funkce y = f(x) má velice jednoduchý tvar: y = 2. Integrační interval je od x = 1 po x = 5. Obsah obdélníka je na první pohled jasný, je to 8 plošných jednotek. Aby nám výpočet sedl na předem známý výsledek musí integrál z dx být x; tedy pokud zvolíme nejjednodušší tvar primitivní funkce.
Další plochou, jejíž obsah spočteme, bude trojúhelník, viz obrázek D. Křivka y = f(x), vlastně přímka, tvořící přeponu trojúhelníka, je dána rovnicí y = x – 2. Pokud nevěříte, dosaďte si za x = 0 a vyjde vám, že y = –2; pak y = 0 a vyjde vám, že x = 2. Jak je vidno z obrázku, přímka těmito body prochází. Obsahu našeho trojúhelníku je roven 2 plošným jednotkám. Z tohoto předem známého výsledku je odhadnut i integrál funkce x, vychází, že je x2/2. Obecně: integrál funkce xn je xn+1/n+1.
Je otázkou, zda nějak takhle matematici kdysi hledali primitivní funkce. Popravdě ani pomyslet. Využívají již zmíněného faktu, že inverzní operací k integrování je derivování: derivace F (x) = f(x). Ze znalosti derivací některých funkcí se odvodí tzv. základní integrály a další integrály se již počítají různými technikami s využitím základních integrálů. Příklad na využití derivace: když vím, že derivace x je 1, tím okamžitě vím, že integrál z 1.dx, což je integrál z dx, je x. Podobně, když vím, že derivace x2/2 je x, tak lehce spočtu integrál z funkce x, je x2/2.
V dalším již takhle složitě integrály konkrétních funkcí počítat nebudeme, tj. ze znalosti obsahu plochy dedukovat jako Sherlock Holmes výraz pro primitivní funkci. Náš cíl je daleko skromnější. Chceme pochopit, co to vůbec integrál je a k čemu může být v nepraktickém životě dobrý.
Na obrázku E si ukážeme výpočet obsahu kruhu pomocí integrálu. Tvar křivky y = f(x) je odvozen z rovnice kružnice. Spočteme si obsah pouze horní poloviny kruhu, který pak vynásobíme dvěma a dostaneme celou plochu kruhu. Tahle malá finta nám umožní vyhnout se znaménku mínus u funkce y = f(x). Integrační interval je jasný, od –r po +r. Výpočet integrálu z odmocniny r2 – x2, zde není uveden, vážný zájemce jej najde v každé učebnici integrálního počtu nebo ve vysokoškolské učebnici matematické analýzy. Výpočet není až tak triviální, používá poměrně náročné techniky výpočtu. Pro nás je ale důležitý jenom výsledek. Výsledný integrál v sobě obsahuje i funkci arcsin, což je cyklometrická funkce.
Jenom malé opáčko. Jistě víte, že sinus je trigonometrická funkce. Pro určitý uhel hledáme daným předpisem definovanou hodnotu, např. sinus 90° je +1. Arkussinus, zkratka arcsin, je inverzní funkce k sinus. Při arcsin je zadána nějaká hodnota z oboru hodnot funkce sinus, tj. od –1 do +1, cílem je najít odpovídající uhel, pro nějž platí, že sinus určeného úhlu se rovná zadané hodnotě z oboru hodnot funkce sinus, např. pro +1 to je 90°. Matematici, ale i fyzici více než stupňovou míru milují míru obloukovou, v ní je např. úhel 90° roven pi/2. V našem příkladě bychom napsali výsledek takhle: arcsin1 = pí/2 (v jazyce internetových stránek, HTML, písmeno pí v řeckém zápisu není k mání). Můžete namítnout, že funkce sinus nabývá +1 i pro další úhly, např. 5/2 pí. Máte pravdu, dokonce pro nekonečný počet hodnot. Jenomže kdybychom uvažovali podobně, tak funkce arkussinus by byla mnohoznačná, a tím by i výsledky vycházely podle toho, který úhel jsme zvolili za výsledek. Aby se takovému mnohoznačnému výkladu zabránilo, funkce arkussinus smí nabývat hodnoty pouze z oboru hodnot od – pí/2 po +pí/2, čímž se stane funkcí jednoznačnou. Pro názornost ještě obrázek z volně dostupných stránek calculatorsoup.com.
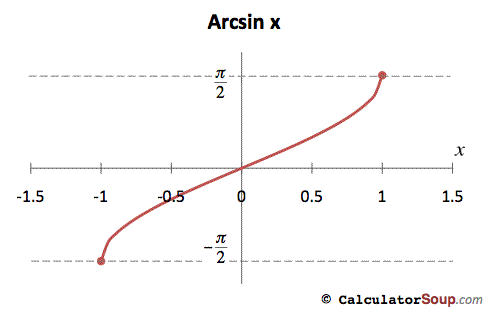
Konečně se dostáváme k výpočtu obsahu kruhu. Vlastní výpočet je na obrázku E, snad je s určitým nadhledem jakž takž uchopitelný. Nakonec cílem tohoto textu není naučit, ale inspirovat.

Poslední výpočet, který si uvedeme, je výpočet obsahu plochy elipsy, viz obrázek F. Popravdě výpočet bude technicky navlas stejný, ale opakování je matka moudrosti. Elipsa má dvě poloosy: hlavní o délce a a vedlejší o délce b. Vidíme, že je to jakási zdeformovaná kružnice. Když do rovnice elipsy dosadíme za a = r a za b = r, dostaneme rovnici kružnice. Z rovnice elipsy je odvozena i rovnice křivky y = f(x). Je velice podobná rovnici kruhu, jenom před odmocninou máme zlomek b/a. Opět spočteme jenom obsah horní poloviny elipsy, čímž se zbavíme i znaménka mínus před celým výrazem. Jistě jste si všimli, že kruh je vlastně speciální případ elipsy, kdy platí: a = b = r. Pokud hodnotu r dosadíme místo a a b do vzorce pro obsah elipsy, dostaneme známý vzorec pro obsah kruhu.

Možná si teď položíte otázku: Mohli bychom pomocí integrálu vypočíst i obvody kružnice a elipsy, když se nám tak elegantně podařilo určit jejich obsahy? Mohli, mohli, ale má to pořádný háček. U kružnice by výpočet zafungoval bez problémů, ale u elipsy by nás čekalo nepříjemné překvapení. Výpočet délky elipsy vede k výpočtu tzv. eliptického integrálu, pro který neumíme najít primitivní funkci, která by se dala zapsat nějak tak "rozumně" jako primitivní funkce vypočtené výše. O co jde přesněji? Když se podíváte na výsledný tvar všech našich primitivních funkcí, tak jsou to, obrazně řečeno, uchopitelné funkce. Podobné funkce nazýváme primitivní elementární funkce. Trochu obecněji: primitivní funkce vytvořena ze základních elementárních funkcí konečným počtem základních aritmetických operací (sčítání, odčítání, násobení, dělení) a tvořením složených funkcí (např. esinx) se zove primitivní elementární funkce. Základní elementární funkce známe již ze střední školy, jsou to: konstanty, mocniny, goniometrické funkce, cyklometrické funkce, exponenciální funkce a logaritmické funkce. Výsledek výpočtu eliptických integrálů nelze vyjádřit jako primitivní elementární funkci, prostě to nejde, a právě proto se k výpočtu eliptických integrálů v praxi používají tabulky. Popravdě znám jenom jednu živou bytost, která v praxi potřebovala spočíst eliptický integrál, ale já to nejsem. Leč proč vždy uvažovat jenom prakticky?
V Brně 12. listopadu 2013.
Doplněk: Pro ty, co jim je funkce arcsinx krajně nesympatická, jsem zařadil do dodatku výpočet obsahu elipsy bez použití této funkce. Navíc oproti předchozím technikám se zde používá substituční metoda, což neznamená nic jiného, než šikovné nahrazení původní integrační proměnné jinou proměnnou tak, aby se výpočet zjednodušil. Ovšem pak je potřeba provést kontrolu hranic integrace, jelikož pro novou proměnnou mohou být jiné. Pokud se nechytáte, nic se neděje, tohle je opravdu jenom technický formální doplněk.
