Kalorimetrie koupelnové vany
Dušan Polanský
Byl jsem požádán, zda bych se nepodíval na problém s napouštěním vody do koupelnové vany. Jak známo, při napouštění vody mícháme teplou a studenou vodu tak, aby teplota lázně vyhovovala našemu tělu. Dokud jsme vanu měli, tak jsem si ji napouštěl dost horkou, po renovaci původního jádra máme již jenom sprchovací kout, takže už si tak moc koupání neužívám, spíš fofruji, abych měl hygienu co nejdříve za sebou.
V zadání, je uvedeno na obrázku č. 2 (číslo obrázku zjistíte po najetí kurzoru myši na obrázek) pod bodem č. 1, je řečeno, že máme k dispozici dvě teplé vody, jedna o teplotě 60 °C a druhá o teplotě 55 °C. Abychom se dopracovali k teplotě lázně, tedy např. k 38 °C je potřeba teplou vodu namíchat se studenou vodou, ta má dle zadání teplotu 15 °C. Otázka je zdánlivě jednoduchá: Jakou teplou vodu je z hlediska energetických úspor k míchání se studenou vodou výhodnější použít, tu o teplotě 60 °C, nebo 55 °C? Je zřejmé, že obecné řešení nezávisí na zde uvedených teplotách.
Také je zřejmé, že je to problém z kalorimetrie. Její název coby součásti nauky o teple, tedy jsme v království fyziky, je odvozen z měření množství kalorií. Kalorie je jednotka energie, ovšem dnes je kalorie většinou nahrazována Joulem, což je jednotka energie v soustavě SI, která platí od roku 1960. Jenom si připomeňme – protože i my budeme důsledně používat jednotky SI –, že základní jednotky v této soustavě jsou sekunda, metr, kilogram, Ampér, Kelvin, mol a kandela. My v našem příkladu si vystačíme s metrem, kilogramem a Kelvinem.
Pokud se nepletu, z kalorimetrie jsme něco málo měli ve fyzice na základce, na stavební průmyslovce jsme měli fyziku jenom jeden rok a navíc chlápek, co nás na fyziku měl, byl vše možné, jenom ne učitel fyziky. Na technické výšce se kalorimetrie nebrala, možná i proto, že kalorimetrie je typická středoškolská látka, ovšem na takové chemické vysoké jistě jí je pozornost věnována. Pokud jde o matematiku, vystačíme si s učivem ze základní školy.
Než se do výpočtů dáme, začneme malým opáčkem té látky z kalorimetrie, kterou budeme potřebovat. Ve Wikipedii se dočteme, že jedna kalorie je množství energie, které dokáže zvýšit teplotu 1 gramu vody ze 14,5 °C na 15,5 °C. No a jelikož víme, že měrná tepelná kapacita vody je asi 4185 J·kg−1·K−1, platí, že 1 cal je cca 4,185 J. Jinak měrná tepelná kapacita látky je množství energie, kterou musíme dodat tělesu o hmotnosti 1 kg, abychom jeho teplotu zvýšili o 1Kelvin. Když už jsme u Kelvinu, Kelvin je jednotka termodynamické teploty, je rovna zlomku 1/273,16 termodynamické teploty trojného bodu vody. Ze základky víme, pro přepočet °C na Kelviny se používá pro běžné výpočty konstanta 273 (v současné době přesně 273,15), která se k °C připočte, u čehož i v naší koupelně zůstaneme. V praxi se při běžných výpočtech měrná tepelná kapacita vody uvažuje 4200 J·kg−1·K−1 a hustota vody 1000 kg m−3, tedy že 1 litr vody má hmotnost 1 kg.
Lze říct, že základ celé kalorimetrie stojí na dvou vzorcích, ty jsou uvedeny na obrázku č. 1. První vzorec, viz bod č.1, je určen k výpočtu energie potřebné k ohřátí určité látky o dané měrné tepelné kapacitě a dané hmotnosti o daný počet Kelvinů. Druhý vzorec, viz bod č. 2, definuje vztah platný pro vyrovnání teplot mezi dvěma látkami o různých teplotách a všeobecně i různých měrných tepelných kapacitách a hmotnostech. Na levé straně rovnice je teplo do soustavy dodané látkou o hmotnosti m1, měrné tepelné kapacitě c1 a teplotě T1. Na pravé straně teplo spotřebované látkou o hmotnosti m2, měrné tepelné kapacitě c2 a teplotě T2. Podle první termodynamické věty po krátkem čase v této soustavě nastane rovnovážný stav, kdy obě tělesa mají stejnou teplotu T. Tento vzore lze jednoduše zobecnit i pro více látek. V bodě č. 3 je uveden jednoduchý příklad na aplikaci vzorce uvedeného v bodě č. 2. Jelikož mícháme dvě stejné vody o různých teplotách, měrné tepelné kapacity nám ve výsledném vzorci vůbec nefigurují.

Konečně můžeme přistoupit k řešení našeho problému. Ovšem ve fyzice bychom nikdy neměli na problém vlítnout jako D’Artagnan na svého stařičkého Žluťáka, kterého mu daroval jeho otec. Napřed si musíme ujasnit potup řešení, nakonec to dělá každý, kdo něco praktického v životě řeší. Je jasné, že když budeme napouštět vanu teplou vodou o teplotě 60 °C, této vody bude potřeba méně než vody o teplotě 55 °C. Jenomže na ohřátí určitého množství vody na 60 °C je potřeba více energie než na ohřátí stejného množství vody o teplotě 55 °C, takže tímto se výhoda úspory teplé vody určitě alespoň částečně neguje. Intuitivně tušíme, že při malém rozdílu teplot 55 °C a 60 °C výsledek energetických úspor bude velmi těsný, navíc když si uvědomíme, že vztahy v našich vzorcích jsou lineární, přesněji se jedná o nepřímou úměru – ušetření teplé vody, zvyšuje v stejném poměru energetickou náročnost na její ohřátí – neměl by být rozdíl dokonce žádný, tedy když připustíme malé rozdíly v důsledku zaokrouhlování výsledku, měli bychom se dopracovat k stejným výsledným hodnotám. Leč uvidíme, jak to dopadne.
Abychom se přesvědčili, zda je naše úvaha správná, zaprvé spočteme potřebné množství teplé vody u obou teplot, a zadruhé výpočtem podle vzorce z obrázku č. 1 z bodu č. 1 určíme, kolik energie budeme potřebovat na ohřátí příslušného množství studené vody na příslušnou teplotu teplé vody. V praxi našeho příkladu je realita taková, že jednoduše spotřebitel vodu o teplotě 55 °C nebo 60 °C dostává z vně námi řešeného systému. Abychom mohli počítat konkrétně, budeme uvažovat, že do vany chceme napustit 100 l vody, což je hmotnost 100 kg.
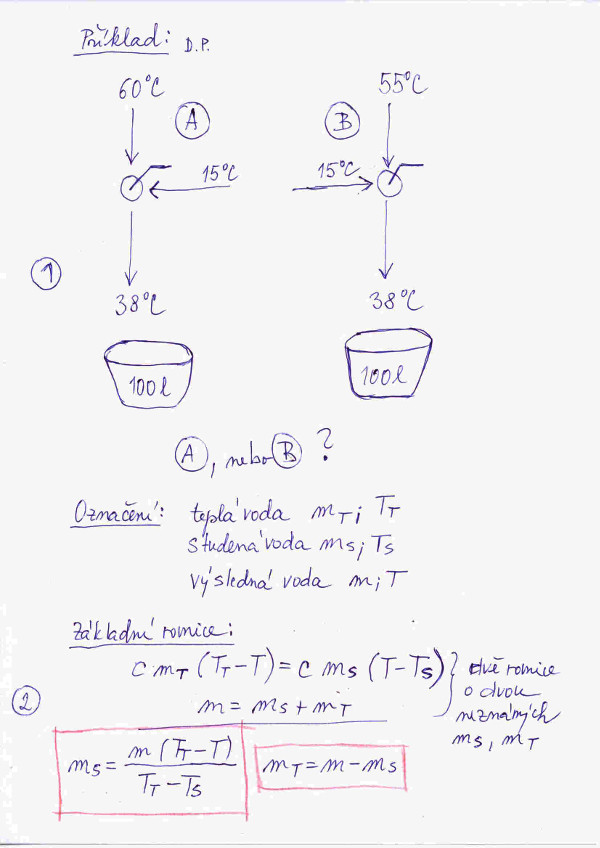
Obecné řešení problému je uvedeno na obrázku č. 2 v bodě č. 2. Není to nic jiného než do našeho problému přepsaná rovnice pro vyrovnávaní teplot. Navíc zde máme další rovnici pro množství teplé a studené vody, jejich součet musí nám dát 100 l, tedy 100 kg. Tím jsme se dopracovali k řešení jednoduché soustavy dvou rovnic o dvou neznámých. Zde uvádím jenom výsledek, ale výpočet doporučuji si provést z cvičných důvodů coby vzpomínku na poslední ročník základky. No a když by s řešením byly problémy, podívejte se na řešení na obrázku č. 4.
Takže obecné řešení máme, teď již jenom budeme dosazovat příslušné hodnoty. Můžete použít excel, ale bohatě postačí i kalkulačka. Konkrétní výpočty jsou vidět na obrázku č. 3. Výpočet je proveden nejen pro teploty ze zadání, ale pro zajímavost i pro teplotu 70 °C. Při zanedbání efektu zaokrouhlení vidíme, že použití té či oné teplé vody nám nepřináší žádnou energetickou úvahu. Proč tomu tak je? Proč nám vyšel stejný výsledek? Jako by vzorec pro Q nezávisel vůbec na teplotě přiváděné vody! A opravdu nezávisí!

Podívejte se na obrázek č. 4, bod č. 2. Q závisí pouze na rozdílu T a TS, vůbec ve vzorci nefiguruje TT! Proč? Protože množství teplé vody je již zohledněno v množství vody potřebné na ohřátí lázně na teplotu T! Čím je TT teplejší, tím méně litrů této vody je potřeba! Vidíme, že jsme si mohli ušetřit pracné výpočty na obrázku č. 3. Stačilo spočíst Q podle vzorce Q = cm (T-TS), což nám dá stejnou hodnotu, k jakým jsme se dopočítali na obrázku č. 3. Přiznám se, že schválně jsem to vzal velikým obloukem, aby bylo vidět, že někdy člověk na první pohled určitou zákonitost nemusí objevit, ale konkrétní výpočty ukazují, že tam přece jenom je, což ho přiměje pokusit se dopracovat k výsledku jinou cestou. V našem příkladu se to povedlo.

Jenom dodejme, že z hlediska technického opotřebení použitého instalačního materiálu není jedno, zda napouštíte více či méně teplou vodu. Teplejší voda dává obvykle ventilům a těsněním více zabrat, protože je agresivnější.
Zdánlivě jsme počítali hodně zbytečně, ale zase na druhé straně, člověka nic tak nepotěší, jako když si praktickým výpočtem potvrdí to, co intuitivně tuší. No a nakonec, proč i nějak takhle neobjevovat krásu fyziky, v našem případě kalorimetrie!
V Brně 9. března 2020.