Objem n-rozměrné koule
Dušan Polanský
Zbytečný úvod
V těchto nelehkých covidových časech a až doteď za ne příliš hezkého počasí se člověk potřebuje něčím zabavit. Čumět stále do počítače či mobilu nebo na TV asi také nebude dobré předsevzetí. Ti, co žijí v rodinném domě se zahradou, či na chalupě nebo v obyvatelné chatě někde v přírodě jsou na tom o poznání lépe, mohou být více na luftu a mít více pohybu. My v panelácích jsme na tom po této stránce hůře, pokud se chceme hýbat, musíme vyrážet na procházky do přírody. Ovšem po takové procházce či dělání něčeho kolem nemovitosti nezaškodí opět se něčím duchovním rozptýlit. A proč ne výpočtem objemu n-rozměrné koule? Sice takový výpočet je k ničemu, ale člověk je tvor, ktorý občas s potěšením dělá i věci bez praktického významu, ale přitom takové, že jej potěší. Takže pokud máte základní znalosti z integrálního počtu, zvu vás na malý výlet do n-rozměrného prostoru. Jelikož nejsem matematik, ale důchodce směřující neodvratně k pozemskému zániku výklad bude volnější. Ovšem to by nemělo až tak vadit, jelikož nemyslím, že text budou číst matematici, ti by podobné texty měli pro nás spíš psát a ne je číst v podání málem sedmdesátiletého plešatého a unaveného laika.
Pointa
Náším cílem je najít vzorec pro výpočet objemu n-rozměrné koule v n-rozměrném prostoru, často se takové kouli říká hyperkoule. Ze základní školy známe vzoreček pro výpočet obsahu kruhu. Kruh můžeme chápat jako 2-rozměrnou kouli v rovině, tedy v 2-rozměrném prostoru. Na obrázku č. 1 (číslo obrázku zjistíte po najetí kurzoru myši na obrázek) je výpočet obsahu kruhu pomocí integrálu. Proč něco počítat jednoduše, když to jde také složitě!

Teď si ukážeme na obr. č. 2, opět s pomocí integrálu, výpočet objemu klasické koule, jak ji např. známe u řádně, podle normy, nafoukaného fotbalového míče. Je zajímavé, že výpočet je o něco jednodušší než u kruhu, což je ale dáno tím, že již umíme spočíst obsah kruhu.
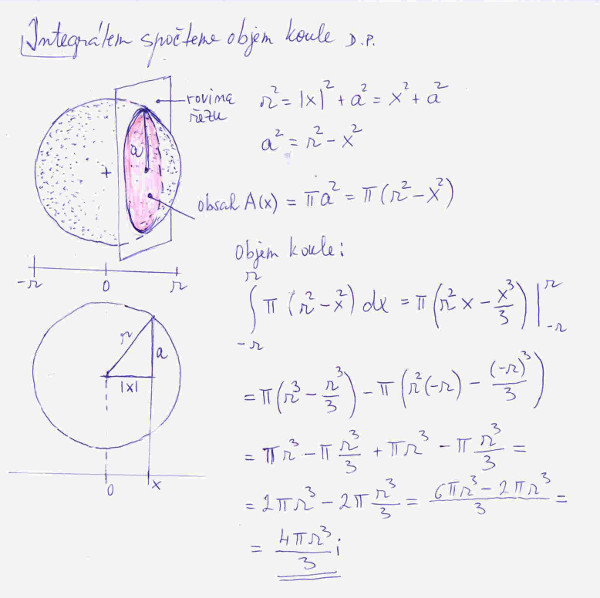
Co můžeme zatím konstatovat? Že objem koule je přímo úměrný mocnině poloměru toho řádu, objem (u kruhu tomu říkáme obsah) kolikarozměrné koule chceme spočíst. U kruhu je plocha úměrná r2, u koule r3. Koeficient úměrnosti je u kruhu pí, u koule 4/3pí. Lze předpokládat, že to tak nějak podobně dopadne i u n-rozměrné koule, tedy že bude objem úměrný rn a opět tam bude figurovat jistý koeficient. Označme si tento koeficient písmenem C s příslušným indexem rozměru, tedy C2, C3 až Cn. Pokud bychom ve vzorcích pro obsah či objem uváděli místo r průměr d, tak příslušný koeficient by musel být vždy menší než 1, např. u kruhu by byl pi/4. Proč? Kdyby byl 1, tak bychom spočetli obsah příslušného čtverce, do kterého je kruh vepsán, přitom víme, že obsah kruhu je vždy o něco menší než obsah příslušného čtverce. Ale my v dalším nebudeme pracovat s d, ale zůstaneme dle zvyklostí u r a navíc nám to zjednoduší výpočty integrálů.
Než budeme pokračovat dále, musíme formálně vyřešit problém s označením rozměrů. V třírozměrném prostoru obvykle značíme pravoúhlé souřadnice písmeny x, y a z, potažmo stejně příslušné pravoúhlé souřadnicové osy. Ovšem ve vícerozměrných prostorech je užitečně zavést praktičtější označení souřadnic, potažmo příslušných souřadnicových os. Značíme je: x1, x2 až xn. Poznamenejme, že matematici občas pracují i s nekonečně rozměrnými prostory, někdy se jim říká Hilbertovy prostory. Po této čistě formální poznámce si na obrázku č. 3. udělejme malou reakapitulaci toho, co zatím víme, potažmo toho co nevíme. Hlavně si pozorně přečtěte text uvedený pod bodem 4. Je zde uvedeno, jak lze formálně vypočíst koeficient C2 v třírozměrném prostoru v případě, že kouli protneme rovinou ve vzdálenosti x od středu kruhu. Tuhle úvahu jsme již použili při výpočtu objemu 3-rozměrné koule. A jak asi již tušíte, na téhle úvaze postavíme výpočet hledaných koeficientů v n-rozměrném prostoru. Opět n-rozměrnou kouli protneme rovinou a náš výpočet bude analogií výše uvedeného výpočtu objemu koule. Je zřejmé, že průnik bude koule o jednom rozměru menším. Její poloměr není veliký problém spočíst, jak vidíme v bodě č. 1.

Na obrázku č.4 je zmíněný postup popsán pro n-rozměrnou kouli. Nejprve určíme objem koule mezi rovinami, které jsou ve vzdálenosti od středu x1 a (x1 + dx1). Pokud střed koule bude v počátku a meze integrace budou od -r do +r, měli bychom se dopracovat k výsledku, ovšem za podmínky, že se nám podaří spočíst integrál uvedený pod písmenem A.

Výpočet zmíněného integrálu je uveden na obrázku č. 5. Postup je opět analogií techniky výpočtu objemu koule na obrázku č. 2. Jediný problém je, že narazíme na integrály uvedené pod písmenem (b). Obvykle jsou spočteny v každé podrobnější učebnici integrálního počtu, výpočet sice není složitý, ale poměrně dlouhý. Na konci obrázku je uveden vztah mezi koeficienty Cn a Cn-2, což je přímo výborné, tedy pokud si uvědomíme, že pokud známe hodnotu koeficientů C2 a C3, postupně můžeme spočíst i objem jakkoliv rozměrné koule. Na základě těchto hodnot a vztahu mezi koeficienty Cn a Cn-2 lehce můžeme spočíst objem 4-rozměrné koule, potažmo 5-rozměrné koule, a pak mohu pokračovat dále. Ovšem tenhle postup je trochu pracný, spíš bychom uvítali univerzální vzorečky pro sudé a liché hodnoty Cn.

Jak se tedy alespoň intuitivně dopracovat k těmto univerzálním vzorečkům? Náznak takového postupu je uveden na posledním obrázku, tedy obrázku č. 6. A tím máme počty za sebou.

A co závěr? Z matematiky raději již nic, stejné nám v covidové době ničím nepomohla, maximálně trápí žáky a studenty. Spíš si přejme, aby covidová doba konečně skončila, a my mohli vyrazit do přírody, na zahrady, na víkendy či dovolené k moři nebo do hor či na chaty nebo chalupy. No a kdo to štěstí či možnost nemá, alespoň do své oblíbené hospody či vinotéky. Očkování, Hospodin a zdravý rozum nám k tomu všem pomáhej.
V Brně 23. března 2021.