Příklad na použití křivkového integrálu
Dušan Polanský
Ve škole se v matematice obvykle počítají spíš školské příklady než příklady alespoň částečně propojené s realitou. Logiku to má, člověk se stane učitelem hlavně proto, že nechce hlavně s běžnou, nemluvě o výrobní, realitou moc mít. Škola je již ze své podstaty speciální typ skleníku, podobně jako státní správa. To není kritika, jenom konstatování určitého sociologického faktu.
Proč o tom vůbec píši? Čtenář asi mající zálibu v chemii, což já vůbec nemám, se na mě obrátil ještě na jaře letošního roku s prosbou, zda bych se nepodíval na jeden příklad z knihy [1] na straně 52, že třebaže je příklad vyřešený, že přesto se téměř nechytá. Sken zmíněné stránky mi poslal e-mailem. Hned mi bylo jasné, že to není čistě matematická úloha, protože byla v tom i termodynamika. Řešení je v knize podáno přímočaře, není uveden každý detail výpočtu, jelikož autoři oprávněně předpokládají, že student zvládl předchozí látku. Popravdě nejprve jsem chtěl čtenáře odbýt, což by nebylo poprvé ani naposled, přece nejsem žádná matematická charita, navíc na matematiku sáhnu v poslední době velice sporadicky a moje hlava my v 67 už také nepodává žádné oslňující výkony, natož když je nepodávala ani v mladších letech. A koneckonců proč bych měl pro někoho počítat nějaký příklad. Leč nakonec mi to nedalo a nad příkladem jsem se zamyslel. Zde je jeho zadání:
Vypočítejme práci, kterou vykoná 1 mol ideálního plynu při přechodu ze stavu M = (P1, T1) do stavu N = (P2, T2) po úsečce MN. P je tlak a T teplota plynu.
Po chvilce dumání jsem pochopil, že tento příklad, ač má jednoduché zadání, je docela náročný nejen na znalosti z matematiky, ale řešitel musí něco znát i z fyziky. Člověk musí umět trochu derivovat, trochu integrovat, dokonce umět spočíst jednoduchý křivkový integrál, umět parametrizovat přímku, no a v neposlední řadě alespoň něco málo znát z termodynamiky. Pokud si vzpomínám na vysokou školu, tak termodynamika se mi jevila nejtěžší z celé fyziky, vyžaduje totiž dost abstraktní myšlení. Abych to nedramatizoval, nakonec jsem čtenáři slíbil, že příklad v dohledné době na svých stránkách podrobně vysvětlím (nejsem ani učitel, ani matematik), aby měl jakous takous šanci příklad pochopit. Dohledná doba trvala dost dlouho, jelikož celé léto jsem promarodil, pobýval jsem dvakrát v nemocnici a absolvoval několik vyšetření. Sice výsledek nic moc, ale znáte to, v 67 již člověk nemůže počítat ze zázraky, natož když genetický základ nic moc. Prostě na výpočet došlo až teď.
Postup bude takový, že si nejdříve zhruba povíme, co je to úplný diferenciál, poté si spočteme nějaký příklad na křivkový integrál, abychom získali minimální rutinu potřebnou pro výpočet křivkového integrálu v našem příkladu. Poté si stručně vysvětlíme, co to znamená parametrizovat přímku, a jak se to dělá. No a nakonec vyzbrojeni tímto aparátem se vrhneme na řešení příkladu.
Proč právě úplný (často i nehezky totální) diferenciál? Jde o to, že křivkový integrál budeme počítat z výrazů ve tvaru P(x,y) dx + Q(x,y)dy, matematici podobným výrazům říkají diferenciální forma. V tomto výraze se mění současně proměnná x i y, žádná z nich nemá privilegované postavení. Ve škole se obvykle setkáváme se zadáním funkce ve tvaru y = f (x), kde x vystupuje jako nezávislá proměnná, kdežto y jako závislá proměnná. Pokud se nezmění x, s proměnnou y se nemůže nic potenciálně dít. Výrazy tvaru P(x,y) dx + Q(x,y)dy mají ve fyzice, speciálně hlavně v termodynamice, veliké uplatnění, jde o to, že pokud derivace P(x,y) podle y se rovná derivaci Q(x,y) podle x, a pokud křivka leží v jednoduše souvislé oblasti, tak hodnota křivkového nezávisí na volbě cesty z bodu A do bodu B. Pokud výraz P(x,y)dx + Q(x,y)dy splňuje uvedenou podmínku, tak se mu říká úplný diferenciál, kupříkladu (6xy2 – y3)dx + (6x2y – 3xy2)dy je takovým diferenciálem. Kupříkladu i gravitační nebo elektromeagnetické jsou příklady polí, kde vynaložená energie na přenesení břemena z bodu A do bodu B nezávisí na tvaru cesty přenosu, tedy na tvaru integrační křivky. V takových případech mluvíme o potenciálových polích. Zmínil jsem jednoduše souvislou oblast. Představte si oblast, v níž leží uzavřená křivka, kterou lze pohodlně stlačovat. Pokud ji dokážete stlačit do bodu, aniž byste se dostali mimo oblast, v níž křivka leží, tak táto oblast je jednoduše souvislá. Jedná se o topologický pojem. Topologie je obor matematiky, podobně jako např. numerická analýza.
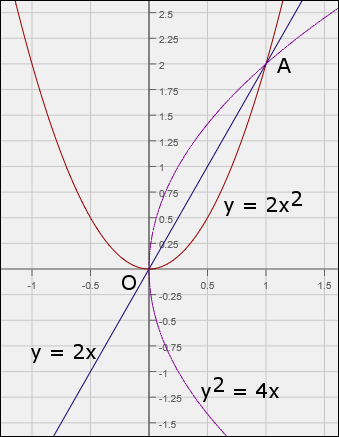
Konečně začneme i něco počítat. Pro zajímavost si spočteme křivkový integrál, jehož výsledná hodnota bude záviset na integrační cestě, tedy integrovaný výraz nebude úplným diferenciálem. Zadání příkladu jsem vzal z [2] z příkladů k samostatnému řešení. Výsledek mého snažení je ve shodě s výsledky uvedenými na konci knihy. Popravdě jsem si vybral nejjednodušší příklad, když už se tak chválím. Na obrázku č. 1 (číslo obrázku se zobrazí po najetí myši na obrázek) vidíte průběh integračních cest, které spojují body O a A. Průběh velice jednoduchých funkčních závislostí jsem nakreslil s použitím grafického editoru [3]. Vlastní řešení vidíte na obrázku č. 2. Hlavně si všímejte triku, kterými jsem výrazy pod integrálem převedl na řešení integrálu, kde integrujeme podle jedné proměnné. Tento trik využijeme i při řešení našeho příkladu. Pokud jde o znalosti integrálního počtu, vystačíme s integrálem funkce xn.
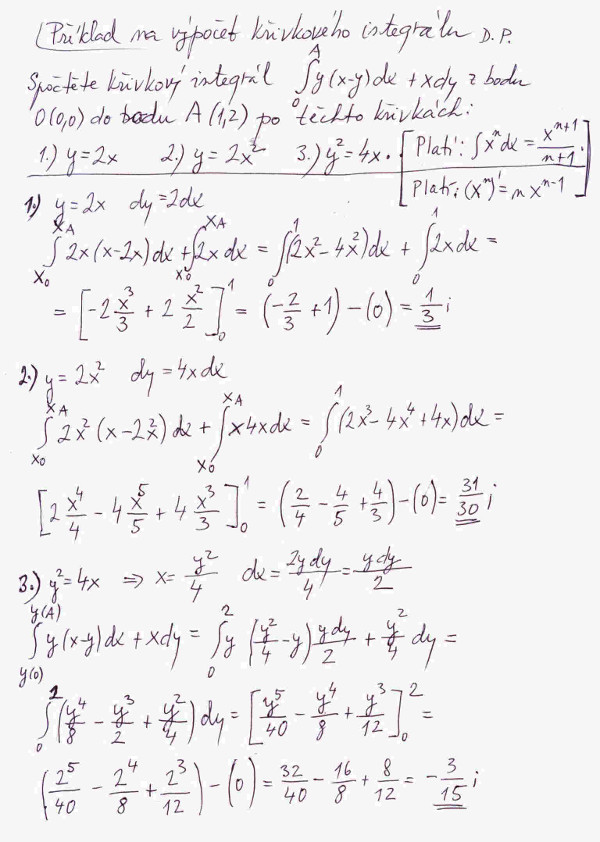
Pokud jde o parametrizaci přímky, vše by snad mělo být zřejmé z obrázku č. 3. Parametrizace přímky se běžně učí na střední škole. Jak je z příkladu patrno, stejnou přímku lze parametrizovat nekonečně mnoha způsoby, jenom vybrat ten, který se co nejvíce hodí na řešený problém.

Než se pustíme do vlastního řešení, dvě malé odbočky do světa termodynamiky. Ovšem nebudeme dokazovat, že stavová rovnice pro 1 mol ideálního plynu zní PV = RT.
První odbočka. Proč vůbec v našem příkladu vystupují dvě stavové veličiny (tlak a teplota)? Proč ne např. tři? O tom kolik, rozhoduje Gibbsův fázový zákon: Obsahuje-li systém f fází a k složek, pak počet stavových veličin postačujících k určení stavu tohoto systému je dán vzorcem v = k – f + 2. V našem příkladu k = 1 a f = 1, z čehož plyne, že v = 2.
Druhá odbočka.Budeme potřebovat vzoreček pro práci vykonanou plynem při jeho expanzi. Zkusme si tento vzoreček odvodit. Nech náš systém je válec s pístem, uvnitř válce je plyn pod tlakem P. Nechť se plyn ve válci rozpíná a nech se posune o malou délku dl, čímž vykoná práci dA = Fdl. Při ploše pístu S můžeme psát dA = PSdl, ovšem Sdl = dV, takže dA= PdV.
Vlastní řešení příkladu je na obrázku č. 4. Výpočet jsem provedl podrobně a snad i jasně. Jedno důležité upozornění pro vlastníky zmíněné knihy: autoři (jak je zřejmé z řešení zmíněného příkladu) důsledně pracují s pojmem vektorového pole, takže výpočet v knize má formálně jiný zápis než ten můj. Tomuto zápisu jsem se úmyslně vyhnul, abych nemusel zavádět a vysvětlovat pojem vektorového pole. Budiž mi to odpuštěno. A to je vše.

Literatura a pomůcky:
[1] Kolda S., Krajňáková D., Kimla A.: Matematika pro chemiky II, Praha, SNTL/ALFA, 1990. Strana 52, příklad 6.25.
[2] Zaporožec G. I.: Rukavodstvo k rešeňju zadač po matematičeskomu analizu, Moskva, Vysšaja škola,1964. Strana 320, zadání příkladu č. 876. Výsledek téhož příkladu na straně 473.
[3] https://www.meta-calculator.com aplikace: graphing-calculator.
V Brně 1. listopadu 2019.