Laplaceův a Gaussův integrál
Dušan Polanský
Střípek málokdy píšu tím stylem, že si řeknu: O tomhle jsem ještě nepsal, tak něco vyplodím. Obvykle je to jinak, k psaní mě inspiruje něco z mého okolí. Podobně je to s tímto textem.
V létě jsem byl s vnoučaty v zoologické zahradě u nás v Brně. Nebyla to ničím výjimečná návštěva, chodíme tam poměrně často, takže někdy už ani nekoukáme na zvířata či ryby nebo plazy, ale kupříkladu skončíme v bufetu u piva a limonád a vnoučata si hrají vedle na písku nebo se předvádí na tribuně. Pokud Zoo v Brně neznáte, podél některých prohlídkových tras jsou i klasické dřevěné černé školní tabule, vždy dvě vedle sebe. K dispozici je běžná bílá školní třída, kyblík s vodou a hadr na umytí tabule. Jedna taková dvojtabule je u pavilonu s ptáky a rybami. No a právě k těmto tabulím se vnoučata rozběhly, že si budou kreslit. Obě byly fest počmárané a pokreslené. Čekalo mě umytí obou tabulí. Když jsem přišel blíže, uviděl jsem na jedné tabuli úplně nahoře napsán velice úhledným písmen tvar Laplaceova integrálu a jeho výsledek. Ve Wikipedii se lze dočíst, že Pierre Simon de Laplace (1749–1827) byl francouzský astronom, fyzik, matematik a politik.
Obě tabule jsem poctivě umyl až na zmíněný integrál. Poté co tabule uschly, výsledek jsem smazal, což bylo formální, jelikož výsledek znám zpaměti – jak za chvíli uvidíte, je velice lehce zapamatovatelný –, vzal jsem křídu a že se dám do výpočtu. Postup výpočtu jsem znal, takže jsem měl docela slušnou šanci dopracovat se k výsledku. Jenomže k výpočtu nedošlo, malý Toník, v té době měl dva a půl roku, ukazujíce na hadr a tabuli začal vykřikovat: Děda, tři, děda tři, což v překladu do řeči dospělých znamená: Děda, utři tabuli! Na své tabuli nechtěl mít nic, chtěl si ji počmárat komplet sám, což u malých dětí není nic neobvyklého. Vojtíšek s Jindrou také odmítly jakékoliv moje zásahy do plochy jejich tabulí, přitom Jindra si zabrala hned dvě odvrácené strany.
Jelikož k výpočtu jsem se nedostal, sedl jsem si na lavičku a ledabyle jsem pozoroval kreslířské výkony vnoučat. Od houpačky stojící kousek bokem, houpaly se na ni dvě větší děti, popošel ke mně starší pán; mohl mít tak sedmdesát. Jak jsem si již všiml předtím, sledoval pozorně celé dění u našich tabulí. S úsměvem na tváři mě pozdravil a sdělil mi, že si všimnul, že jsem integrál nesmazal a že jsem jej chtěl spočíst. Zda jsem matematik nebo učitel? Ne, ne, kdepak, s matematikou nemám nic společného, vystačil jsem celý život s kupeckými počty. To jenom občas, náhodně, obyčejná zábava. Začal mi vyprávět, že učil na základní i střední škole matematiku, ale že na integrál na tabuli, také si jej všimnul, by si netroufl. Že sice na střední škole občas základy integrálního počtu učil, ale integrál na tabuli nikdy se studenty nepočítal. Ještě doplnil, že i teď si přivydělává doučováním matematiky, že hlavně doučuje středoškoláky. Ještě chvíli jsme si kolem matematiky povídali, ale pak moje dcera zavelela, že nastal čas dát se na pochod domů. Se starším pánem jsem se rozloučil a slíbil jsem si, že výpočet integrálu z tabule si do konce roku na své stránky dám. Takže proto tohle zbytečné matematické povídání. Zbytečné proto, že výpočet Laplaceho integrálu je v každé slušnější knize o integrálním počtu. Výpočet lze dohledat i na internetu. Problém je jediný, že autoři většinou vypustí detaily výpočtu, že přece to je každému jasné, a také neuvedou, jaké znalosti jsou k výpočtu potřeba. Já tyhle trapné samozřejmosti nevypustil a ještě jsem přidal něco navíc.
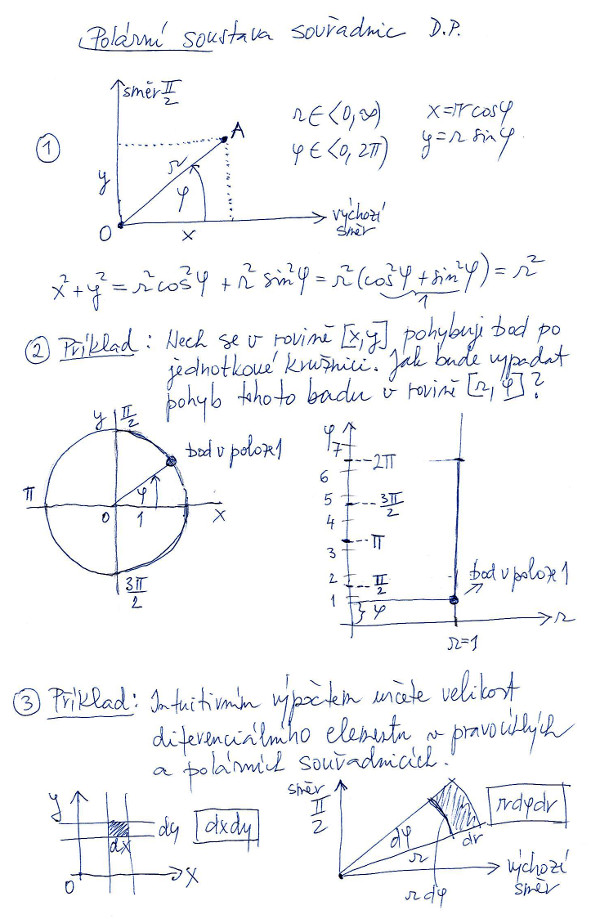
Po neslušně dlouhém a vyčerpávajícím úvodu se konečně dostáváme k matematice. Jaké znalosti jsou k porozumění tohoto textu potřebné? Přibližně na úrovni elementárního úvodu do diferenciálního a integrálního počtu. Vše, co budeme k výpočtům potřebovat, jsem shrnul na obrázcích č. 1 a č. 2; číslo obrázku zjistíte po najetí myší na obrázek. Z pokročilejších technik integrálního počtu používáme pouze větu o derivaci integrálu, její znění je na obrázku č. 2, ale k této větě se ještě vrátíme.
K stručné rekapitulaci znalostí, o nichž bychom měli mít alespoň tucha. Hodně budeme využívat polární souřadnice. Na obrázku č. 1 v bodě č. 1 je jejich definice. V bodě č. 2 je příklad na zobrazení pohybu bodu po jednotkové kružnici v polárních souřadnicích. V bodě č. 3 je intuitivní výpočet vzorce pro diferenciální element (diferenciální znamená malinkatý až mrňavý) v pravoúhlých a polárních souřadnicích. Intuitivní výpočet proto, že kdybychom byli matematici, ale my nejsme, správně bychom měli spočíst tzv. Jakobián polárních souřadnic. Pokud se právě teď nechytáte, nic se neděje, vystačíme si s našim intuitivním odvozením na obrázku.
Na obrázku č. 2 v bodě č. 1 je malé opáčko k derivování exponenciální funkce, pochopitelně ne náhodně, ale proto, že exponenciální funkci derivovat budeme. Podobně budeme potřebovat spočíst integrál, v němž integrovanou funkcí bude právě exponenciální funkce, výpočet je uveden v bodě č. 2. Pod bodem č. 3 je uvedena věta o derivaci integrálu podle parametru, jež se obvykle v základním kursu integrálního počtu neprobírá. Důležité si je uvědomit, že zde derivujeme podle parametru a, ne podle proměnné x. Za chvíli uvidíme, jak se tahle technika při praktickém výpočtu poměrně složitého integrálu dá využít.

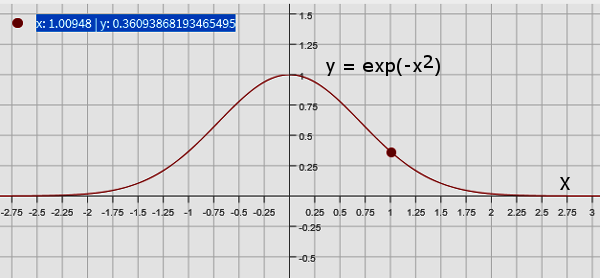
Na obrázku č. 4 je úplně nahoře uveden tvar již zmíněného Laplaceova integrálu. Než se ale pustíme do jeho výpočtu, sluší se vědět jak graf funkce, s jejíž integrací se budeme trápit, vypadá. Zobrazen je na obrázku č. 3. Pro nakreslení obrázku s rastrem v pozadí jsem použil volně dostupný webový program www.meta-calculator.com. Texty jsem doplnil volně dostupným programem GIMP. Když si graf nakreslíte, můžete v zmíněném obrázku využít automatický odečet hodnot x a y. Stačí myší pohybovat po křivce funkce, viz hodnoty pro jeden takový bod na modrém pozadí.
Jazykem geometrie jednoduchý integrál není nic jiného než výpočet obsahu plochy ohraničené v našem případě osou x a grafem funkce. I v matematice, podobně jako v technických vědách, by mělo platit, že než se na příslušný výpočet vrhneme, měli bychom se pokusit výsledek alespoň přibližně odhadnout. Když se na obrázek č. 3 pozorněji podíváme, zdá se, že obsah by neměl být větší než 2, ale měl by být větší než 1,5 plošných jednotek. Také tušíme, že obsah asi nebude vyjádřen konečným číslem, jelikož graf se podél osy x táhne do nekonečna v kladném i záporném směru. Uvidíme, zda naše intuitivní, čistě laické úvahy mají hlavu a patu.
Na obrázku č. 4 je výpočet Laplaceova integrálu proveden fintou přes zavedení polárních souřadnic. Na výpočet se jde oklikou, místo I počítáme integrál I2. Poté si zavedeme polární souřadnice, které nám výpočet zjednoduší. Pro vyřešení integrálu, který nám po zavedení polárních souřadnic z toho vylezl, použijeme substituci a nakonec vyřešíme jednoduchý integrál, v němž integrandem je funkce e-u. Integrál z téhle funkce již spočíst umíme, viz obrázek č. 2. Konečný výsledek je odmocnina z čísla pí. Na Základní škole jsme se učili, že číslo pí je iracionální, což znamená, že jej nelze vyjádřit zlomkem m/n, kde m je celé číslo a n přirozené číslo, takže výsledek Laplaceova integrálu je rovněž iracionální číslo, operace odmocnění nemůže na tom nic změnit. Pokud jde o obsah plochy pod vyšetřovanou funkcí, opravdu je někde mezi 1,5 a 2; o něco přesněji a přibližněji na 6 desetinných míst je obsah 1,772453.

Zvládnouce hravě Laplaceův integrál, zkusíme spočíst Gaussův integrál, viz obrázek č. 5. Ve Wikipedii se dočteme, že Johann Carl Friedrich Gauss (1777–1855) byl geodet, astronom a fyzik, ale především geniální matematik. V našem výpočtu se budeme snažit určit velikost konstanty K tak, abychom normalizovali integrál na pravé straně, tedy aby pravá strana jako celek nám dala 1. Výpočet je téměř navlas identický s výpočtem Laplaceova integrálu. Vidíme, že velikost konstanty K a tedy i počítaného integrálu, kde integrand má tvar -1/2ax2, je odmocnina z 2pí/a, přitom uvažujeme a > 0. Opět nám vyšla iracionalita, jako kdyby těch iracionalit nebylo dost v našich životech, ještě se s nimi potkáváme i v matematice.

A na závěr ještě něco těžšího, viz obrázek č. 6. Vidíme, že v integrandu je navíc výraz xn, kde platíˇ: n > -1, alfa > 0. Pro všechna n s našimi znalostmi výpočet nezvládneme, uvidíme že pouze pro nulu a sudá čísla. Integrál budeme řešit ve dvou krocích. V prvním kroku spočteme integrál bez xn. K tomu využijeme znalost výpočtu Laplaceova integrálu. V druhém kroku využijeme již výše zmíněnou větu o derivaci integrálu podle parametru, viz obrázek č. 2 bod č. 3. Jednoduše levou i pravou stranu musíme derivovat podle parametru alfa, přičemž x zde nevystupuje jako proměnná, ale jako konstanta, proměnnou je právě parametr alfa. V bodě č. 3 jsme se pokusili o jakési zobecnění našeho výsledku, viz vzorec s červenou svislicí vlevo. Výpočet pro jedničku a lichá čísla není také vůbec složitý, zvládli bychom jej pomocí integrace per partes, ale tuhle techniku jsme si zde nevysvětlili, takže výpočet vypouštíme.

Možná se teď ptáte, kde člověk narazí na tak relativně složitou funkcí jako je funkce v našem posledním integrálu. Kupříkladu při řešení kvantového harmonického oscilátoru. Pokud mi nevěříte, zadejte si do google.com heslo quantum harmonic oscilator a podívejte se na tvar výsledních vlnových funkcí. Pochopitelně nic takového v praktickém životě (u zkoušky z kvantové mechaniky na výšce budiž) nepotřebuje 99,999 % obyvatel Země, ale znáte to, lidé se baví ve volnu všelijak, tak proč ne právě výpočtem podobných integrálů. Dodejme, že námi spočtené integrály mají široké uplatnění nejen v čisté matematice, ale i ve fyzice, v teorii pravděpodobnosti, v teorii chyb atd. Koneckonců kdyby nebyly tak důležité, tak bych o nich nepsal. A to je vše.
V Brně 2. listopadu 2017.