Nejen o lineárním programování
Dušan Polanský
Zbytečný prolog
S matematikou je jeden veliký problém, většina lidí v životě vystačí s kupeckými počty, takže o důležitosti matematiky lze přinejmenším diskutovat. Ne jinak je tomu u většiny matematiků, protože matematiku jenom učí a v reálu používají opět jenom kupecké počty. Osobně matematické znalosti nepovažuji o nic důležitější než jakékoliv jiné znalosti, dokonce si myslím, že pro život jsou matematické znalosti spíš nedůležité. Ovšem to mi nebrání, abych se občas matematikou coby formou duševní relaxace nepobavil. Nedávno jsem byl k takové relaxaci tak trochu nepřímo vyzván. Kolega programátor mi povídá, že slyšel, jak se dva maníci bavili o lineárním programování, ale přitom o žádném programování – tak jak jej on programátor zná – nebyla řeč. Usmál jsem se a řekl mu, že vím, o čem je řeč. A začal jsem psát. Popravdě to ale nebyl jediný důvod, ten druhý snad pochopíte, pokud si přečtete i epilog.
Lineární programování je i není programování. Pod programováním si obvykle představujeme psaní programu v nějakém programovacím jazyce, ale žádné obavy, program psát nebudeme, to by nám ještě scházelo, vždyť programátorský chleba není žádný med. My jenom využijeme program, který již někdo kdysi napsal a je k dispozici v Excelu. Pokud jde o znalosti, vystačíme se znalostmi ze základní školy. Kde to bude potřeba, nějakou tu matematickou maličkost si dovysvětlíme.
Vše začalo po válce, u nás pak v 60. a v 70. letech. Do módy se dostaly matematické metody, které měly podpořit optimalizaci všeho možného, hlavně minimalizaci nákladů, a tím i maximalizaci zisku. Jednou z takových metod je i lineární programování. Jinak v zahraniční literatuře tyhle metody obvykle najdete v učebnicích finitní matematiky, do které kromě toho obvykle patří základy kombinatoriky, teorie pravděpodobnosti, teorie Markovových řetězců a procesů a teorie her. V letech 1971 až 1976 jsem studoval na vysoké vojenské škole v Žilině a také jsme měli dva semestry přednášek a cvičení ze zmíněných matematických metod, předmět měl název Základy teorie riadenia. Matně si vzpomínám, že na ústní zkoušce jedna z třech otázek zněla: Vysvětlite princip dynamického programování, a to bylo moje štěstí, jelikož dvě předchozí otázky nic moc, popravdě ani se nebylo co divit, přípravu na zkoušku jsem zcela odbil. Nakonec jsem zkoušku měl za dva. V té době se na vysoké hodnotilo takto: za jedna, za dva, za tři a pak již jenom vyhazov ze zkoušky.
Pokud se zeptáte, zda jsem někdy prakticky něco z optimalizačních metod v profesní praxi natvrdo použil, férově odpovím, že ne. Ale když jsem sloužil ještě jako voják z povolání, v jedné ze stovek 24 hodinových služeb, které jsem odsloužil, jsem měl pomocníka důstojníka v záloze. Byl to náměstek v jakémsi podniku a všimnul si, že si jen tak z dlouhé chvíle listuji v jakési populární matematické knize. Rozmluvil se, že by chtěl v podniku zracionalizovat rozvoz produkce, což je problém z teorie grafů a pak částečně i z lineárního programování. V té době jsem si z této problematiky ze školy už toho moc nepamatoval, matematice je tak pro zábavu jsem se vůbec nevěnoval, jelikož dálkové studium, malé děti a časově náročná služba mi to absolutně nedovolovaly, proto jsem mu jenom laicky – podobně jako je napsán tenhle článek – vysvětlil, jak by asi mohl problém uchopit. Asi za dva měsíce se mi ozval, že mu moje informace pomohli problém vyřešit. O několik let později jsem znalost lineárního programování využil pro oživení elementárního úvodu do Excelu, v rámci vysokoškolského předmětu Základy informatiky. V tom předmětu se probíralo snad všechno letem světem, což chronicky nesnáším. Do základů sice tahle látka nepatřila, ale mně se zdála docela zajímavá, tak jsem ji do výuky zahrnul. Studentům popravdě látka moc neseděla, hlavní problém měli se sestavením matematického modelu problému, viz dále. U zkoušky jsem znalost téhle látky proto raději nepožadoval. Nakonec i dobrý kuchař by se měl přizpůsobit chutím strávníků.
Jádro povídání
Takže po vcelku zbytečném úvodním povídání přistoupíme k lineárnímu programování. Vše si ukážeme na jednoduchém příkladu, který je zadán tak, aby nám vyšel hezký lehce ověřitelný výsledek. Podívejte se (zatím nic nepište!) na obrázek č. 1 (číslo obrázku se vám zobrazí po najetí myší na obrázek), je na něm vidět v netextové podobě zadání. Jádro zadání je podbarveno žlutě. Vyrábíme dva druhy výrobků, k výrobě každého potřebujeme určité množství každé suroviny (množství jsou uvedené v žlutě podbarvené tabulce úplně nahoře). Každé suroviny máme k dispozici jenom určité množství (12 a 8). Dále víme, jaký zisk máme z každého výrobku (z prvního 3 peněžní jednotky, z druhého jenom 2). Náš problém zní:Kolik výrobků každého druhu máme vyrobit, abychom maximalizovali náš zisk? Když budeme znát počty výrobků, spočíst zisk je již jednoduché.
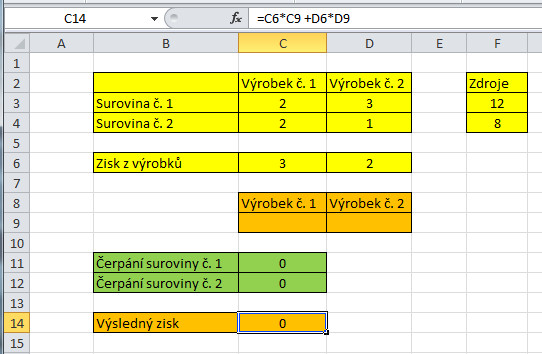
Při řešení podobných optimalizačních problémů si je potřeba nejdřív ujasnit zadání, v dalším kroku pak sestavit matematický model problému. Třetí krok spočívá ve vyhledání programu, který by za nás po dosazení správných hodnot spočetl. V době, kdy jsem studoval v Žilině, jsme vlastní výpočet museli oddřít ručně. Mohu vás ujistit, že je to hrozná otrava, protože je kolem toho dost teorie z lineární algebry a technika výpočtu není až tak jednoduchá, takže je veliká pravděpodobnost, že se člověk sekne. K obrázku č. 1 se ještě vrátíme, pro pochopení zatím stačí to, co vidíme. Posledním krokem při řešení jakéhokoliv problému je správná interpretace výsledku. Což nemusí být vždy až tak jednoduché, stačí si vzpomenout, jak je někdy složitá názorná interpretace vzorců ve fyzice.
Problém jsme snad pochopili a můžeme přistoupit k sestavení matematického modelu. Zatím neznámý počet výrobků č. 1 si označíme x, neznámý počet výrobků č. 2 písmenem y a zisk P. Naším cílem je maximalizovat tzv. účelovou funkci P = 3x + 2y. Proč, dědo? Jak by se zeptal vnouček Vojtíšek. Protože zisk z výrobku č. 1 jsou 3 peněžní jednotky a z výrobku č. 2 jsou 2 peněžní jednotky. Jaká další omezení klademe na proměnné x a y. Určitě musí být větší nebo rovné nule, protože záporný počet výrobků vyrobit neumíme. Ale to není vše, máme omezené zdroje surovin. Omezení jsou dvě: 2x + 3y musí být menší nebo rovno 12 a 2x + 1y musí být menší nebo rovno 8. Na obrázku č. 2., viz níže, je zcela nahoře napsaný náš matematický model. Sumárně model tvoří jedna lineární rovnice, tzv. účelová funkce, a čtyři lineární nerovnice. Lineární proto, že x a y vystupují v rovnici a nerovnicích jenom lineárně, proto také mluvíme o lineárním programování. Naším cílem je maximalizovat hodnotu P. Teoreticky teď již stačí spustit Excel, vyvolat správný program, do něho dosadit správné vstupy a Excel by nám měl vychrlit výsledek, tedy x a y, při nichž bude P v rámci dostupných zdrojů surovin maximální.

Než tak učiníme, zkusme problém vyřešit graficky bez Excelu. Snad nám to pomůže hlouběji pochopit základní myšlenku lineárního programování. Předtím ale mále opáčko z geometrie. Ze základní školy si jistě pamatujete, že přímka v rovině má rovnici Ax + By + C = 0, kde A nebo B musí být různé od nuly, kdyby A a B byly současně nuly a C by bylo různé od nuly, vyšel by nám nesmysl. Obrazem nerovnice, v níž vystupuje rovnice přímky v rovině, je plocha nad a pod přímkou, případně i samotná přímka pokud nerovnost obsahuje i znaménko =. Přímka v rovině se kreslí docela příjemně. Stačí do rovnice přímky dosadit x = 0, tím dostaneme bod, kde přímka protíná osu y, pak dosadíme y = 0 a dostaneme bod, kde přímka protíná osu x. No a dvěma body v rovině již přímku umíme nakreslit. Přímky z našeho matematického modelu vidíte nakreslené modře na obrázku č. 2.

Intuitivně je asi zřejmé, která nerovnost z našeho matematického modelu graficky znamená plochu nad a která pod přímkou. Matematika sice s intuicí a citem pracuje, dokonce podle slavného důkazu Kurta Gödela z roku 1931 ani jinou volbu nemá, ale bez důkazů to v matematice ve většině případů přece jenom nejde. Triviální důkaz toho, že pod respektive nad přímkou se opravdu rozumí pod respektive nad přímkou přesně tak, jako tyto pojmy chápe i dítě ve školce je uveden na obrázku č. 3. Přímka na obrázku má rovnici 2x + 3y = 12, její konstrukce je snad jasná z výpočtu, který je uveden pod rovnicí přímky v rámečku. Na přímce jsme zvolili libovolný bod P(x,y). Bod P1 má souřadnice (x,y1), a protože y1 > y určitě 2x + 3y1 > 12. Z toho plyne, že všechny body plochy nad přímkou splňují nerovnost 2x + 3y > 12. Podobná úvaha platí pro bod P2. Ten má souřadnice (x,y2), a protože y2 < y určitě 2x + 3y2 < 12. Z toho zase plyne, že všechny body plochy pod přímkou splňují nerovnost 2x + 3y < 12.
Čtyři neostré nerovnosti z matematického modelu vymezují v rovině vytečkovanou plochu z obrázku č. 2. Určitě v této ploše bude ležet řešení, které nám přinese maximální zisk. Jak jej ale najít? Zkusme do účelové funkce P = 3x + 2y dosadit hodnotu P = 6, pak P = 10 a obě přímky vynést do obrázku č. 2. Na obrázku jsou vytaženy červenou barvou a označili jsme je L1 a L2. Všimněme si, že směrnice (tedy sklon přímky vůči ose x) je u obou rovnic stejný. Proč? Protože sklon přímky závisí pouze na koeficientech u neznámých x a y. Zkuste si přepsat rovnic 6 = 3x + 2y do tvaru y = kx + q. Písmeno k v této rovnici je směrnice přímky. Do podobného tvaru si přepište rovnici 10 = 3x + 2y. Zjistíte, že k, tedy směrnice přímky je obou přímek stejná, mění se pouze hodnota q, která definuje vzdálenost od počátečního bodu, kde přímka protíná osu y. My chceme pochopitelně najít řešení, kde hodnota neznámé P bude co největší, protože P je zisk. Když se pozorně podíváme na obrázek č. 2, tak se zvyšující hodnotou P se přímka rovnoběžně posouvá dále a dále od počátečního bodu. Nám jde o to, aby se výsledná přímka dotýkala co nejvzdálenějšího bodu tečkované plochy od počátku, protože pak hodnota P bude jistě největší, protože x a y budou v rámci tečkované plochy největší možné. Najít v našem příkladu takový bod nebude až tak těžké. Vidíme že je to ten bod, kde se protínají přímky 2x + y = 8 a 2x + 3y = 12. Souřadnice tohoto bodu lehce zjistíme řešením soustavy těchto dvou rovnic o dvou neznámých. Kupříkladu tak, že z první rovnice vyjádříme y a dosadíme tenhle výraz za y do druhé rovnice, čímž z ní dostaneme rovnici o jedné neznámé x. Řešením téhle rovnice nám vyjde x = 3. Pak za x dosadíme do první rovnice hodnotu 3 a spočteme y. Vyjde nám, že y = 2. Takže zmíněný, námi hledaný, bod má souřadnice P(3,2).
Teď přistoupíme k interpretaci výsledku získaného grafickou cestou. Co v našem modelu vyjadřuje bod P(3,2)? O neznámé P víme, že vyjadřuje hodnotu zisku. Xová souřadnice bodu P je 3, ypsilonová je 2. Ale co jsou v našem příkladu x a y? Jsou to počty výrobků č. 1 a č. 2. Takže bod P(3,2) nám říká, že při x = 3 a y =2 by měl být zisk maximální. Jaký náš zisk bude? Zjistíme to jednoduše, do rovnice P = 3x + 2y dosadíme za x počet 3 a za y počet 2. P nám vyjde 13 peněžních jednotek. Určitě nás nepřekvapí, že rovnice červeně nakreslené přímky, L3, procházející bodem P(3,2), je právě 13 = 3x + 2y. Rovněž lehce zjistíme, že při počtu výrobků 3 a 2 vyčerpáme zcela oba zdroje surovin, stačí hodnoty 3 a 2 dosadit do nerovnic, které popisují omezení pro zdroje. To jistě zvládnete i sami.
Máme vyhráno? Jenom částečně. Naše úloha je velice jednoduchá, kdyby došlo na lámání chleba, dala by se vyřešit i metodou pokus omyl. V reálném světě jsou zadání daleko složitější, matematický model může obsahovat i desítky nerovnic a účelová funkce bude ve většině případů obsahovat více než dvě proměnné. Daleko efektivnějším řešením je využití programu, který umí řešit úlohy lineárního programování. Takových programů je na trhu hodně, ale my bohatě vystačíme s Excelem, který obsahuje doplněk Řešitel a tento Řešitel zase obsahuje program, který umí řešit lineární úlohy. K tomu používá algoritmus založený na tzv. simplexové metodě.
Teď si ukážeme, jak se řeší naše úloha v Excelu. Opět musíme mít k dispozici matematický model problému, bez toho se z místa nepohneme. S vytvořením matematického modelu vám žádný program na světě nepomůže. Tento model jsme si v našem případě vytvořili. Teď nám půjde o to, jak tento matematický model šikovně zadrátovat do Excelu a jak vyvolat Řešitele a donutit jej problém vyřešit. Uvidíme, zda nám dodá stejné výsledky jako grafické řešení.
Než se do toho dáme, malé upozornění. Standardně Řešitel v Excelu není k dispozici, je to doplněk, který si musíte aktivovat. V Excelu 2003 se to dělá tak, že zvolíte ve vodorovné nabídce Nástroje >> Doplňky, tam si zaškrtněte Řešitel a volbu potvrďte OK. V Excelu 2010 dosáhnete stejného efektu přes Soubor >> Možnosti >> Doplňky. Takže budeme předpokládat, že Řešitele máme k dispozici (v Excelu 2003 v záložce Nástroje, v Excelu 2010 v záložce Data).
A konečně můžeme přistoupit k vložení zadání do Excelu, viz obrázek č. 1. Vše to, co je ve třech žlutých tabulkách jednoduše opíšete. Dále tam máme dvě buňky C9 a D9, do těch nám Řešitel po výpočtu zapíše počty výrobků č. 1 a č. 2. Tyto dvě buňky necháme prázdné. Zelenou barvou máme vyznačené buňky C11 a C12, do těch vložíme vzorce popisující čerpání zdrojů, tedy surovin č. 1 a č. 2. Co je zapsáno v buňce C11? =C3*C9 + D3*D9. Co je napsáno v C12? =C4*C9 +D4*D9. To, co je napsáno v buňce C14 vidíte na obrázku, je to účelová funkce z našeho modelu.
Než si spustíme Řešitele a vyplníme to, co bude od nás požadovat, zkusme selskou úvahou dojít na to, co bude od nás chtít. Určitě bude chtít adresu buňky, kde je vložená definice účelové funkce, jinak by těžko spočetl zisk a nevěděl by, co má maximalizovat. Také bude chtít vědět, kam má vložit hodnoty vypočtených neznámých, tedy počty výrobků č. 1 a č. 2. Jistě budeme muset do Řešitele vložit čtyři nerovnosti z našeho modelu. Dvě pro omezení zdrojů a dvě pro nezápornost počtů výrobků. A nakonec mu sdělíme, jakou metodu výpočtu má použít, protože těch metod umí více.
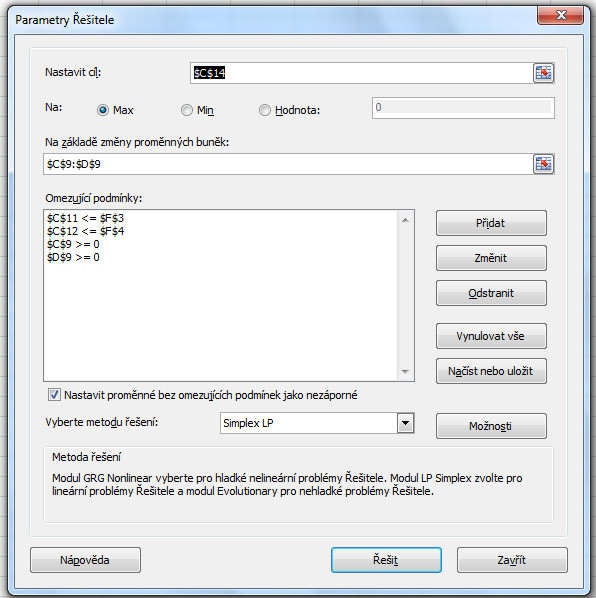
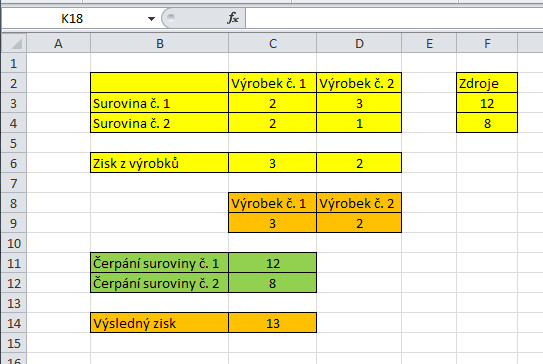
Na obrázku č. 4 vidíte, co jsme nakonec kam do Řešitele doplnili. Obrazovka je z Excelu 2010, v Excelu 2003 je vizuálně trochu jiná, ale kritická pole pro vložení stejného matematického modelu jsou tam stejné. Logika výpočtu je stále stejná bez ohledu na použitý nástroj. Metodu výpočtu jsme zvolili Simplex LP. Proč? Ve vysvětlujícím textu je nám doporučeno použít tuto metodu pro řešení lineárních problémů, a náš problém takový je. Pak by již mělo stačit kliknout na tlačítko Řešit a Řešitel by nám měl doplnit do našeho listu, počty výrobků a zisk. Pokud by na vás řešitel vychrlil nějakou divnou hlášku o buňce, ignorujte ji. Před vlastním zobrazením výsledků se vás ještě Řešitel zeptá, jak má s řešením naložit. Zvolte volbu Uchovat řešení řešitele. Na posledním obrázku, tedy č. 5, konečně vidíme výsledek výpočtu. A hle, výsledek našeho grafického řešení je ve shodě s řešením Řešitele. Skvělé! No a to je fakticky vše. Teď už víte o lineárním programování přesně to, co já.
Snad ještě malá technická poznámka. Zde nám počty výrobků vyšli vzorně celočíselné a vyčerpali jsme do puntíku i oba zdroje surovin. V reálu to bude spíš výjimka. Hodnoty neznámých nám vyjdou často necelá čísla. Pak je potřeba z výsledku vzít jenom celé části, problém to není, protože Excel má funkci =CELÁ.ČÁST. Pochopitelně zisk musíme pak spočíst pouze z celých hodnot, ne z těch s desetinnými místy, které nám dodá Řešitel.
Zbytečný epilog
Na lineární programování mám i jednu velice smutnou vzpomínku. V průběhu studií v Žilině, pak po skončení školy a nastoupení do zaměstnání v Brně, a hlavně při služebních cestách do Prahy se mi podařilo zkompletovat všecku literaturu k matematickému programování, jehož podmnožinou je i lineární programování, co u nás do té doby vyšla, tedy asi do roku 1977. Další zakoupené tituly byly hlavně z diferenciální geometrie, některé opravdu vzácné ještě z doby, kdy se skripta psala volně rukopisem bez psacího stroje. Byl tu ale jedne problém, kam s nimi. V Žilině jsem 5 let bydlel na internátě a v Brně po škole asi 14 měsíců na ubytovně, proto mi nezbývalo nic jiného než mít knihy u rodičů v Malackách. Byt byl sice malý, ale patřily k němu dva sklepy. V jednom jsem si udělal vysoký regál, do něhož jsem knihy ukládal. Ke konci roku 1977 jsem dostal výměr na vojenský být, nic velikého, ale bylo to poprvé v mém životě, kdy jsem měl své soukromí. Hned poté, co jsem si koupil na půjčku velikou knihovnu, vzal jsem veliký kufr a vyrazil k rodičům, že si vlakem převezu přibližně první třetinu knih do Brna. Jenomže čekalo mě smutné překvapení: knihy byly pryč a místo nich v regálu stály sklenice se zavařenými okurkami. Přitom ve sklepe místo ještě bylo, jenom to chtělo udělat si regál. Vše skončilo ostrou hádkou s otcem. Zeptal jsem se ho, kde knihy skončily. Že postupně je vyhazoval do popelnice. Od rodičů jsem si nevzal od 19. let ani korunu, jediné co jsem chtěl, abych dočasně mohl mít u nich uložené ve sklepě knihy do doby než dostanu byt. Pak jsem si již nikdy žádnou knihu z matematického programování ani diferenciální geometrie nekoupil. I tenhle čánek byl napsán z hlavy, pouze zadání jsme měl ještě z dob vysokoškolské výuky načmárané na á čtyřce. V hranaté závorce jsem měl pro kontrolu uveden správný výsledek.
Jenomže Boží mlýny melou tragikomicky spravedlivě i tehdy, když nikdo o žádnou spravedlnost moc nestojí. Když táta zemřel, přispěl jsem penězi bratrovi výrazně na zařízení pohřbu, pořízení hřbitovní desky a zaplacení pronájmu za místo odpočinku. Bratr totiž žil u rodičů a pracoval tam, kde táta měl být pohřben. Asi půl roce po pohřbu jsem byl na služební cestě v Bratislavě a bylo přirozené, že jsem chtěl položit kytku k jeho desce s urnou, ale ani po dvou hodinách hledání se mi nepodařilo najít jeho místo odpočinku. Na správě hřbitova mi bylo sděleno, že do konce úložní doby nikdo urnu nezvyzvednul, takže jeho popel v souladu s příslušným zákonem byl zcela nedávno, tedy a tedy, rozptýlen na rozptylové loučce. Zda se tam chci jít podívat? Přiznám se, že jsem nešel. Kytku jsem položil na hrob mně zcela neznámé mladé dívky. Nevím ani proč, ale v té chvíli jsem vzpomněl na moje knihy, které skončily v popelnici. Tátův popel zase kdesi anonymně na rozptylové loučce. Neskončilo to ani pro jenoho z nás dobře, ale jsme si kvit. Přesně jako v matematické rovnici, kde se levá strana rovná pravé.
Napsáno počátkem listopadu, publikováno 8. 11. 2015 v Brně.