Logaritmus coby určitý integrál
Dušan Polanský
Možná, že dále zmíněnou zkušenost máte i vy. Dáte se do řeči s někým zcela neznámým a po krátkém povídání zjistíte, že přece jen něco společného máte, kupříkladu oba znáte někoho, koho zná každý z vás, byli jste na dovolené na stejném místě, vychodili jste stejnou školu, máte podobné zdravotní problémy, podobnou práci, podobné zájmy, nebo dokonce jste vzdálení příbuzní apod. Ne jinak je to nejednou i v matematice. V tomto povídání si ukážeme souvislost mezi zdánlivě, tedy alespoň na první pohled, rozdílnými funkcemi, a to funkcí inverzní a logaritmickou. Bohužel porozumění vyžaduje elementární znalost teorie určitého integrálu a praxe počítání s ním.
Předstartovní příprava
Začnu učeně. V matematice je řada funkcí, kterou jsou definovány nebo lze je definovat jako určitý integrál s proměnnou horní nebo dolní mezí. Jednou takovou funkcí je i přirozený logaritmus, tedy logaritmus se základem e (eulerovo číslo). Pochopitelně logaritmus se dá definovat i čistě algebraicky, jak se to nakonec děje na střední škole. Nakonec i já jsem jedno takové zcela elementární povídání založené na algebraickém přístupu napsal, viz tento odkaz.
Ovšem určitým integrálem lze definovat i rafinovanější funkce, které jen tak lehce nejde jinak definovat, kupříkladu Legendrovy eliptické integrály, pomocí níž se dá kupříkladu lehce spočíst délka elipsy, tedy když máte po ruce příslušné tabulky.
Onehdy mě napadlo, podívat se, zda někde jsou odvozeny základní vlastnosti logaritmů – jak je známe ze střední školy –, tak že se důsledně pracuje !jenom! s definicí logaritmické funkce určitým integrálem s proměnnou horní mezí. Díval jsem se nejen na naše učebnice, ale kupříkladu i učebnice některých amerických univerzit, mám jich v knihovně několik, a mohu potvrdit, že mají vesměs velice dobrou pedagogickou úroveň, hodně obrázků, často v barvě, plus názornost a jasnost výkladu, ale bohužel, nepodařilo se mi najít to, co jsem hledal. Někde byly základní vlastnosti logaritmů dokázány klasicky algebraicky, někde byly dokázány dvě vlastnosti přes integrální definici a zbývající různými, často umělými triky, až jsem se někdy divil proč tak zbytečně uměle. Pochopitelně nemám k dispozici celý fond učebnic integrálního počtu všech vysokých škol světa, na to by mi ani malý panelákový byt nestačil. Ještě jsem chvíli šmejdil po internetu, ale pak mě to přestalo bavit. Jednoduše jsem vzal papír a propisku a odvodil jsem si to sám.
Ještě na bídné alibi dodám, že na konci výše zmíněného mého článku jsem coby jakýsi nezávislý doplněk sice uvedl definici ln x coby určitého integrálu v mezích od 1 do t pokud t > 0, integrační proměnná tam byla označena jako x, ovšem ale už ne itegrálem, leč diferenciálním počtem je dokázána jedna základní vlastnost přirozeného logaritmu: ln (ab) = ln a + ln b. Ale už tehdy jsem si byl dobře vědom, že je to takové nešikovné škrábání se za uchem přes hlavu, ale někdy účel světí prostředky, chtěl jsem se vyhnout kvůli elementárnosti textu výpočtům pomocí integrálů.
Logaritmická funkce definovaná určitým integrálem
Nejprve se spolu podívejme na obr. č. 1 (číslo obrázku se objeví po najetí kurzoru myši na obrázek).
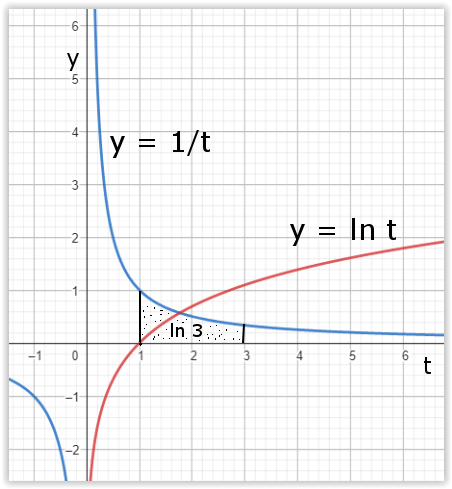
Jsou zde na něm vykresleny fragmenty dvou funkcí, inverzní a logaritmické funkce. Nezávislou proměnná je zde označená jako t; písmenko x si rezervujeme na něco jiného. Na první pohled není mezi funkcemi nějaká souvislost, možná že pro t > 0 hodnoty obou funkcí při přibližování k nule se přibližují více a více k nekonečnu. Sice jedna k plusovému nekonečnu, druhá k mínusovému nekonečnu, a to je tak vše. Zatím nebudeme věnovat pozornost vytečkované ploše s textem ln 3, k tomu se za chvíli dostaneme. A přesto zdání nesouvislosti nás klame, souvislost mezi nimi je totiž veliká. Jaká, to nám hned osvětlí obrázek č. 2.

V něm v bodě č. 1 je uvedena druhá základní vlastnost určitého integrálu, ta první (pro zopakování) nám říká, že určitý integrál funkce f(x) v mezích od a do b, se rovná rozdílu F(a) – F(b), kde F(x) je primitivní funkce k funkci f(x). A právě tahle druhá základní vlastnost nám umožní definovat přirozený logaritmus, tak jak učiněno v bodě č. 2. Všimněte si, že x jsme zde použili pro označení proměnné horní meze, kdežto integrujeme podle proměnné t! Z téhle definice je také hned zřejmý význam tečkované plochy na obrázku č. 1. Její obsah je roven ln 3. Abychom se o tom vizuálně přesvědčili, podívejme se na výstup z grafického kalkulátoru Geogebra na obrázku č. 3.

Zdá se, že integrální definice pro tento případ docela dobře funguje. Ovšem to coby důkaz nestačí, to je jenom jeden jednotlivý případ. Teď nám proto půjde o to, dokázat, že základní vzorečky o vlastnostech logaritmů, které známe již ze střední školy, lze dokázat i pomocí integrální definice logaritmické funkce, teprve tím budeme mít pevnější půdu pod nohama. Na začátku obrázku č. 4 pod písmeny a) až e) jsou tyto vlastnosti uvedené v pořadí, které není až tak obvyklé pro učebnice. Proč asi? Důvod je přísně logický, totiž při odvozování se při tomto uspořádání nebudeme muset odvolávat na ještě nedokázanou vlastnost.
Při dokazování vlastností b) až d) pro výpočet určitého integrálu používáme důsledně vždy nějakou šikovnou substituci, tedy zavádíme místo původní integrační proměnné jinou proměnnou, a jak víme z integrálního počtu, v takovém případě musíme určit nové integrační meze pro tuto novou proměnnou. To je ve výpočtech pečlivě ukázáno a provedeno. Vše vidíme na obrázcích č. 4 až č. 6. Výpočty jsem provedl podrobně, aby si čtenář nekazil náladu zbytečnostmi.
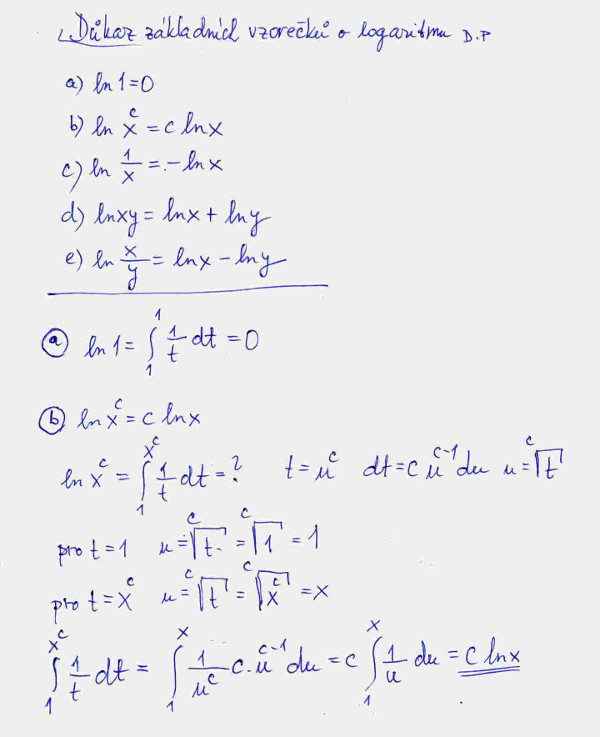
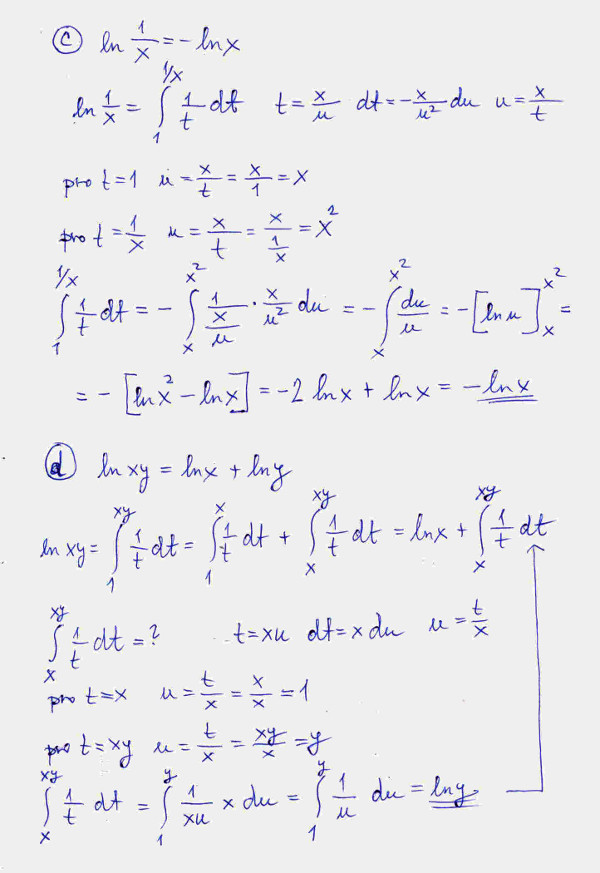

Tím bychom mohli vlastně skončit, jenže pozorný čtenář si jistě povšimne, že naše integrální definice sice platí pro mez x > 0, ale zatím jsme se pohybovali pouze v mezi od 1 do nekonečna. Jak ale je to s hodnotami menšími než 1, ale většími než 0? Můžeme si to představit tak, že změníme integrační hranice, horní mez by byla 1 a dolní x, v tomto případě by se jednalo o určitý integrál s proměnnou dolní mezí, jenomže naše definice logaritmické funkce je definovaná s proměnnou horní mezí! Co s tím?
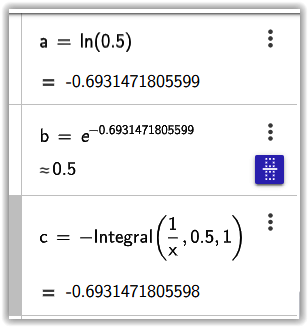
Stačí maličkost! Dobře víme, že když u určitého integrálu zaměníme integrační meze, musíte změnit znaménko celého integrálu. Takže budeme pracovat s mezemi od 0 < x < 1, ale před integrál dáme znaménko mínus. Na obrázku č. 7 je proveden pro porovnání výpočet ln 0,5 jednak kalkulátorem a jednak pomocí integrální definice. Vypadá to, že to funguje i pro hodnoty logaritmu menší než 1. Ovšem kalkulátor Geogebra mi jaksi odmítnul vygenerovat k tomu nějaký obrázek. Budiž jeho vůle, nebo moje neznalost. No, a to je vše. Ani to snad moc nebolelo. Pak mi povídejte, že logaritmus je pěkně hnusný a nesympatický, jak občas studenti tvrdí! Pro mne jsou dalece nesympatičtější těstoviny, které kromě přílohy do polévky téměř nemusím.
V Brně 14. února 2023.