Neoblíbené logaritmy
Dušan Polanský
Za mých středoškolských studií (1967–1971) za logaritmy učily a také prakticky používaly, tedy alespoň na stavební průmyslovce. Bylo to dáno tím, že ještě nebyly kalkulačky a při výpočtech v odborných předmětech se hodně používalo logaritmické pravítko. Výpočty pravítkem byly vždy jenom přibližné, což bylo dáno konstrukcí pravítka a přesností odečtu hodnot ze stupnice, ale dosažená přesnost výpočtů bohatě v stavařských předmětech dostačovala. Pokud jde o tabulky, tak se používaly pětimístné. Opět dosažená přesnost postačovala. Pochopitelně byly k dostání i sedmimístné tabulky, viz např. [2], ale ty se na středních školách obvykle nepoužívaly.
Pokud jde o logaritmické pravítko, nikdo nám nevysvětlil propojení teorie logaritmů s konstrukci pravítka (v slangu logáro), pouze jsme věděli, že hlavní stupnice je logaritmická. Pravítko jsme v odborných předmětech používali mechanicky, ale zase proč ne, většina uživatelů také neví, a popravdě je to ani nezajímá, co se děje uvnitř v počítači, a přesto počítač úspěšně používá. Podobně jako používá např. auto, televizor, lednici, mobil.
Nedávno jsem se dočetl, že logaritmy studenti nemají v oblibě, asi podobně jako nerovnosti s absolutními hodnotami. Moralizovat a mudrovat je zcela zbytečné, s čím se člověk potkává jenom ve škole, ale ne v životě, je a bude vždy neoblíbené, což je nakonec správné. Máme se učit pro život, ne pro memorování, třebaže mnozí učitelé zastávají názor, že škola je také fragment života, takže jaképak copak: Studenti, učte se pro školu!
Jenomže někdy trochu opatrnosti neuškodí ani v matematice, ačkoliv její zamýšlenou maturitní povinnost považuji za dost problematickou. Logaritmům se nedá i přes dokonale kalkulačky a tabulkové procesory (např. Excel) jenom tak lehce uniknout. V pokročilejší fyzice, technických vědách, v teorii informací a chemii na ně narazíte. Takže nebude snad od věci to úplně nejelementárnější si o nich říct, přesněji si zopakovat. K pochopení vystačíme s látkou ze základky, maximálně navíc budeme potřebovat vědět, že např. mocninu 2–n lze zapsat jako 1/2 n.
Většina z nás zcela intuitivně tuší, že obvykle každá matematická operace má i operaci inverzní. Pokud platí c = a + b, např. 10 = 7 + 3, tak pomocí inverzní operace odčítání (–) můžeme zapsat výpočet pro a i b: a = c – b, b = c – a. Pokud platí c = a × b, např. 30 = 3 × 10, tak pomocí operace dělení (/) dokážeme zapsat výpočet pro a i b: a = c/b, b = c/a. Ale teď budeme trochu opatrnější, pokud platí c = ab, kupříkladu 1024 = 2 10 tak bez váhání pomocí operace odmocnění dokážeme vypočíst a jako b-tou odmocninu z c. Ovšem jakou operaci použít pro zápis výpočtu b, tedy exponentu? Právě k tomu slouží operace logaritmus, tedy v zkratce řečeno logaritmus je exponent. Tímto exponentem umocníme tzv. základ, v našem označení a (základ může být principiálně jakékoliv kladné číslo mimo 1), a měli bychom dostat c. V našem numerickém příkladu vyjádříme exponent 10 jako log 21024, což čteme: logaritmus 1024 o základě 2 je 10. Popravdě základ 2 se moc nepoužívá, občas v informatice, ve středoškolské matematice se většinou probírají logaritmy o základě 10, jsou to tzv. dekadické logaritmy (Briggsovy) a značí se log. Hlavně ve fyzice a vyšší matematice se užívá logaritmů o základě e (cca 2,718), takové logaritmy značíme obvykle ln (logaritmus naturalis).
My se sice budeme věnovat dekadickým logaritmům, ale pro názorné vysvětlení vztahu exponenciální a logaritmické funkce se hodí již zmíněné logaritmy o základě 2. Na obrázku č. 1 vidíme vztah těchto dvou funkcí jak v podobě tabulkové, tak i grafické. Vidíme, že jsou symetrické podle přímky y = x, v matematice takovým funkcím říkáme inverzní. Jak jsme se k inverzní funkci dopracovali? Vyšli jsme z exponenciální funkce y = 2x, z té se dostaneme k inverzní funkci (v té vyjádříme zatím čistě formálně x jako funkci y v stejném tvaru jako jsme vyjádřili y) x = 2y, v které ale musíme dát y správnou formu i správný význam. V našem případě to bude y = log2x, což je funkce logaritmická, protože dle definice logaritmu platí, že: x = 2log2x. I proto nás moc nepřekvapí, že v kalkulačce nad klávesou log je napsáno 10x. Všichni víme, že exponenciální funkci (a další funkce napsané nad klávesou) vyvoláme po stisku klávesy 2ndf. Z našeho obrázku je zřejmé, že logaritmická funkce má smysl pouze pro kladná čísla. S nulou jsou jako vždy problémy, protože logaritmus nuly je nehezké číslo: mínus nekonečno.
Trik s vytvořením inverzní funkce si je užitečné zapamatovat, např. velice podobně postupujeme, když chceme vyrobit k funkcím goniometrickýn inverzní funkce, tedy funkce cyklometrické.

Už jsme si řekli, že éra výpočtů pomocí logaritmů skončila s nástupem kalkulaček a počítačů. Do té doby výpočty s velikým čísly, s čísly s mnoha desetinnými místy, složité odmocniny či mocniny se počítali logaritmicky. Kupříkladu když máte ručně pod sebou (dnes to školáci ani moc neumí) vynásobit dvě čísla 25,689 × 56,897 docela se nadřete, kdežto když máte k dispozici logaritmické tabulky výpočet se o něco zjednoduší. Za chvíli si na praktickém příkladě ukážeme, jak se kdysi pomocí logaritmů počítalo, ale napřed si odvodíme základní pravidla pro počítání s logaritmy, protože ty budeme pro naše výpočty potřebovat. Obvykle je studenti znají mechanicky, ale jejich odvození, jak můžete vidět na obrázku č. 2, je poměrně jednoduché. V bodě č. 1 je definice logaritmu, v bodě č. 2 jsou vykřičníkem označené dva důležité vztahy, které jsme si odvodili o kousek výše, akorát tam jsme uvažovali základ 2. V dalších bodech jsou odvozeny základní vztahy pro počítání s logaritmy právě s využitím zmíněných důležitých vztahů. Je intuitivně zřejmé, že sčítání je jednodušší operace než násobení, podobně odčítání než dělení, násobení než umocnění a dělení než odmocnění. No a právě na tyto jednodušší operace se při počítání s logaritmy složitější operace převádějí. V tom je počtářská pointa využití logaritmů.

Teď si ukážeme, jak se s logaritmy počítalo. Jelikož většina z vás nemá k dispozici klasické tištěné Valouchovy tabulky, např. viz [2], popravdě také k čemu, použijeme k tomu vědeckou kalkulačku. Tu má dnes k dispozici každý student. Dokonce přesnost logaritmů získaných kalkulačkou je vyšší než např. v zmíněné literatuře. Výpočty jsou na obrázku č. 3.

V prvním příkladu máme logaritmicky spočíst třetí odmocninu z 729. Předem víme, že je to přesně 9. Jde o to, zda se trefíme do 9 i při logaritmickém výpočtu. Vidíme, že pokud použijeme hodnotu z výpočtu, že jo. Proč? Protože i ta moje levná kalkulačka za necelých 100 Kč při výpočtu pracuje s více číslicemi než zobrazuje na displeji (moje zobrazuje 10 číslic). Pokud nepracujeme s průběžnou hodnotou z předchozích výpočtů, displej vynulujeme klávesou C a zadáme číslo 0,954242509, pak po volbě inverzní funkce 10x, výsledek se k 9 jenom velmi těsně blíží. Vidíme, že logaritmické výpočty jsou často jenom přibližné.
V druhém příkladu máme spočíst hodnotu relativně složitého vzorce. Vzorec jsem převzal z [1], str. 236. Tam je výpočet proveden s využitím pětimístných logaritmů čísel z tabulek, proto i my počítáme s pěti desetinnými místy. Výsledky jsou velice podobné. Je to tím, že pokud počtář v tabulkách nenašel příslušnou hodnotu, tak se dělali poměrně složité interpolace, kdežto my jsme v kalkulátoru jednoduše uvažovali jenom pět desetinných míst bez jakékoliv interpolace či zaokrouhlování.
V posledním, třetím, příkladu máme určit algoritmus čísla 0,42132 na 7 desetinných míst jednak z tabulek [2], a jednak pomocí kalkulačky. Vidíme, že zdánlivě jsou to různé hodnoty, ale opravdu jenom zdánlivě, protože v bezkalkulačkovém věku se používal zápis výhodnější pro ruční výpočty, kdežto kalkulačka nám dá tvar se záporným znaménkem.
No a to je o základech logaritmů z mé strany vše.
Doplněk: Samostatnou kapitolu tvoří logaritmické rovnice, které patří do veliké skupiny funkcí transcendentních (kupříkladu tam patří funkce exponenciální; goniometrické a k ním inverzní funkce cyklometrické). V logaritmické funkci vystupuje neznámá v logaritmu. Často k výsledku vedou šikovné algebraické úpravy. Na internetu je takových rovnic vyřešených habaděj, ovšem jak jsem se zběžně díval, téměř žádná pozornost není věnována rovnicím, jako je např. zdánlivě jednoduchá rovnice: x = 50 * log(x). Tahle má na první mrknutí určitě řešení x = 100, ovšem může mít i jiná řešení, např. přibližné řešení 1,049519. U takovýchto rovnic nám algebraické úpravy nepomohou, musíme zvolit numerické nebo grafické řešení. Je zajímavé, že jsem zvolil v Excelu techniku úmyslných cyklických odkazů, ale na zde uvedenou rovnici technika nezabrala. Kupříkladu rovnici x = cos(x) pomocí iterativních přepočtů (právě ty využívá zmíněná technika cyklických odkazů) Excel hravě zvládnul. Zmíněnou rovnici s logaritmickou funkcí lze ale vyřešit pomocí excelovského doplňku Řešitel. Ale to je již povídání o jiné problematice.
Literatura:
[1] Kudláček L., Válka F., Burian F.: Matematika pro I. a II. ročník studia na středních průmyslových školách pro pracující. Praha 1963, SPN. [2]Valouch M., Valouch M. A.: Sedmimístné logaritmy čísel. Praha 1953, NČAV.
V Brně 31. ledna 2019.
Doplněk z 19. listopadu 1920: Tento doplněk je určen pro ty, co znají základy diferenciálního a integrálního počtu. Jde o to, že přirozený logaritmus (značí se ln) lze zavést pomocí určitého integrálu. Jak se to obvykle dělá, je vidět na obrázku č. 4. Jenom dodejme, že integrál lze definovat tímto způsobem proto, že funkce 1/x je spojitá pro všechna kladná x.

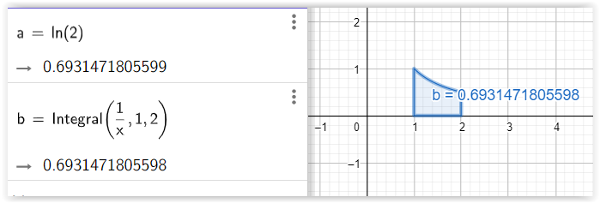
Ovšem vše je potřeba ověřit výpočtem. Na pomoc si vemem program Geogebra. Zkusme porovnat hodnotu ln(2) získanou z kalkulátoru a spočtenou právě zavedeným integrálem. Výsledek tohoto porovnání vidíme na obrázku č. 5. Výsledky se liší až na 13 desetinném místě, což je dáno především způsobem výpočtu hodnot funkce ln(x), které se počítají pomocí nekonečné řady.
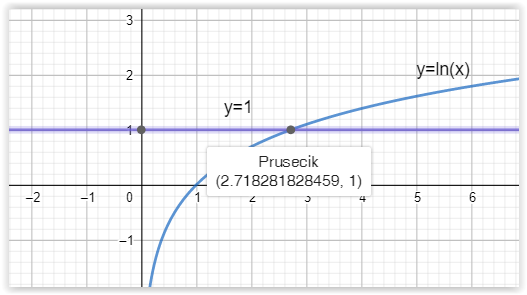
No a protože funkce ln(x) je rostoucí, nabude každé hodnoty pouze jednou. Určitě tedy existuje jediné číslo, v němž ln(x) nabude hodnoty 1. Toto číslo značíme e, a je to číslo důležité nejen v matematice, ale i v technických a jiných vědách. Nelze se pak divit, že má i své vlastní jméno: eulerovo číslo; tak je pojmenováno po významném matematikovi Leonhardovi Paulovi Eulerovi (1707 - 1783). Jaká je jeho přibližná hodnota, můžete vidět na obrázku č. 6.