K čemu je dobrá Lorenzova křivka
Dušan Polanský
Nedávno jsem si na internetu se zájmem přečetl článek Kateřiny Mahdalové: Data odhalují, kolik veškerého majetku v Česku patří skupině nejbohatších. Článek je napsán zajímavě, fakticky a působí věrohodně, což v dnešních časech není až tak běžné. Ovšem u podobných průzkumů se vždy nabízí jedna docela zásadní otázka: Jak se postupovalo při získávání dat, jaká metodika byla použita? To se obvykle nedozvíme. Máme na výběr: věřit, nebo nevěřit. Já tentokráte uvěřil, určitě ne na 100 %, ale nějak tak, že by to tak mohlo s dost velikou pravděpodobností být.
Po přečtení zmíněného článku může zvídavého čtenáře napadnout otázka: A vůbec, jak je u nás rozloženo vlastnictví majetku napříč celým spektrem obyvatel našeho státu? Hned odpovím, že to nevíme, a že to jenom odhadujeme. A vůbec, jde alespoň teoreticky vyjádřit míru rozdělení majetku ve státě nějakým číslem? Tak to víme, a o tom si něco povíme.
Zdůrazněme si, že nás zde nezajímá politikum, tedy jak se kdo k majetku dostal, zda někdo pracovitostí a důvtipem či podfukem nebo darem od státu anebo dědictvím atd. Půjde nám jenom kvantitativní vyjádření míry majetkové nerovnosti.
Pro grafické vyjádření (nejen) majetkových nerovností, potažmo míry koncentrace majetku, se používá Lorenzova křivka. Je pojmenovaná po americkém statistikovy Max Otto Lorenzovi (1876 – 1959). Jinak nerovnosti, potažmo míry koncentrace, mohou být různé, např. podle států rozdělení zásob vzácných prvků, ropy, nositelů Nobelových cen, ale my se raději vrátíme k majetkovým nerovnostem.
Lorenzův návrh byl prostý: roztřídit nositele znaku (v našem případě majetku) podle velikosti, od malých po velké. Podívejme se společně na následující obrázek, a něco si k němu povíme.
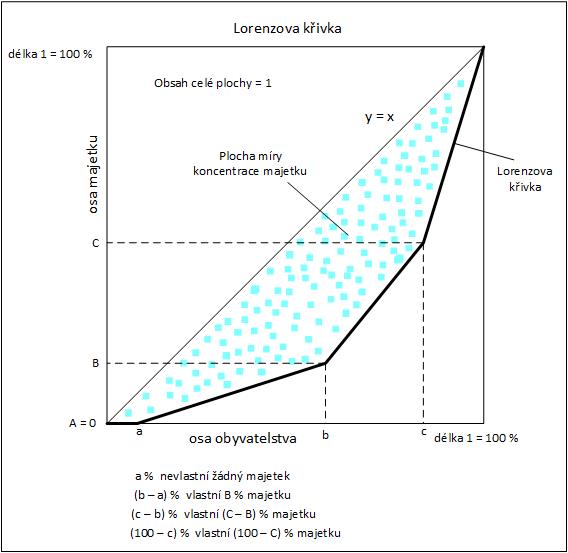
Základem je plocha čtverce o obsahu 1 nějaké plošné jednotky. Čtverec je rozdělen úhlopříčkou (matematicky má rovnici y = x) na dvě stejné poloviny, každá má obsah 0,5. Na osu x vynášíme % obyvatelstva, na osu y % vlastněného majetku z celkového objemu majetku. Podle doporučení pána Lorenze budeme do naší soustavy souřadnic vynášet výši majetku (to je námi sledovaný konkrétní znak) od malých hodnot po velkém. Jsou i lidé, co nemají nic, jejich počet v procentech obyvatelstva nechť je a %, a jelikož nemají nic, mají majetkovou souřadnici (osa y) na 0 %. Dále vidíme, že (b – a) % obyvatel vlastní B % majetku, (c – b) % obyvatel (C – B) % majetku, a nakonec (100 – c) % obyvatel vlastní (100 – C) % procent majetku.
Zmínil jsem křivku, ale co jsem na obrázku tlustě nakreslil je určitě lomená čára. Je to proto, že jsem uvažoval (kvůli názornosti) jenom málo intervalů procentního rozdělení majetku. Pokud by těch intervalů bylo více, už by se naše lomená čára více podobala křivce. V každém případě naše křivka je ohnutá směrem dolu, geometricky řečeno je konvexní. Vidíme, že čím je křivka prohnutější směrem k ose x a prudčeji pak stoupá podle pravé svislé strany našeho čtverce (má rovnici x = 1), tím je rozdělení majetku nerovnoměrnější, neboli koncentrace majetku v rukách jednotlivců je větší, proto se zcela logicky nabízí použít velikost plochy mezi úhlopříčkou a Lorenzovou křivkou jako kritérium majetkové nerovnosti. Tahle plocha je na obrázku vyčtverečkovaná světle modrou barvou. Tahle plocha může být maximálně 0,5 plošných jednotek, a to v případě, že veškerý majetek by vlastnila jedna jediná osoba a my ostatní nic. Druhým extrémem je 0 plošných jednotek, to v případě když Lorenzova křivka se kryje s úhlopříčkou, šlo by o absolutně rovnostářské rozdělení majetku, všichni bychom byli na tom majetkově stejně.
Ve statistice jsou docela oblíbené koeficienty mezi 0 a 1. Proto se obvykle jako míra nerovnosti majetku v praxi používá dvojnásobek míry koncentrace, tzv. Giniho koeficient. Pokud si jej zadáte do vyhledávání ve vašem prohlížeči, zjistíte pro některé státy i jeho hodnoty. Kupříkladu pro Švédsko je to 0,250; pro Německo 0,283; pro USA 0,466; pro Mexiko 0,546; pro Nabimii 0,707. Pokud jde o ČR spíš se odhaduje, že prý je někde mezi 0,2 až 0,3. Ale znáte to, pokud to není podloženo alespoň jakž takž přesnými daty, je to stále jenom prý, a popravdě hádače a filozofy nemám v oblibě.
V Brně 22. ledna 2024.