Mealyho automat
Dušan Polanský
V letech 1978 až 1984 jsem dálkově studoval na VUT v Brně elektronické počítače. Důvod mého studia vůbec nesouvisel se zájmem o počítače, což je ale pro tohle povídání sekundární. Horší bylo, že to byla doba končící vlády velikých a středních sálových počítačů. Jakmile jsme dostudovali, začaly se pomalu prosazovat zcela nové technologie (ty, co dnes kralují), o nichž jsme se na škole nedozvěděli vůbec nic. Studentovi medicíny se to nemůže stát, anatomie a příznaky nemocí se nemění. Evolučně se mění léky, léčební postupy a přístrojové vybavení, ale k těmto věcem se absolventi medicíny pořádně dostanou beztak až po skončení školy v praxi. Nemluvě vůbec o studiu cizích jazyků, jazyk vám nikdo jen tak nezmění.
Specifikem tehdejšího studia na VUT v Brně bylo, že se poměrně veliká pozornost věnovala výuce překladačů. Ovšem, aby jeden pochopil, jak funguje překladač nějakého programovacího jazyka, musí něco znát z formalizované teorie jazyků a gramatik. Je to sice dost podobné jazykům a gramatice klasických jazyků, ale u těch počítačových je vše striktně definováno a formalizováno, de facto je to taková trochu podivná matematika. Abych mohl vykonat zkoušku z gramatiky a jazyků, musel jsem mít nejprve zápočet, jenomže abych měl zápočet, musel jsem vyřešit příklad. Jeho přesné znění si již nepamatuji, ale pointa všech příkladů u tohoto předmětu byla stejná. Na vstupu je jakýsi řetězec znaků a ten se má podle určitých gramatických pravidel transformovat do požadovaného výstupního řetězce. Kupříkladu si představme, že na vstupu jsou znaky –+–+–++156. Je potřeba vymyslet taková pravidla, že pomocí nich transformujeme tento řetězec na správný číselný řetězec s jedním aritmetickým znaménkem, buď +, nebo –, v našem příkladu by to dopadlo takto: –156. Pravidla naší gramatiky musí být tak šikovně vymyšlena, abychom jednak uměli načíst číslice, a jednak se zbavili nějak šikovně všech zbytečných znamének a nechali tam nakonec jenom jedno, to správné. Jinak jazyk tohoto příkladu je velice jednoduchý: jsou to číslice 0 až 9 a znaménka +, –. Bohužel příklad se mi nedařilo vyřešit, jednoduše se mi nedostávalo od Boha příslušného IQ. Již asi od třinácti let jsem si docela přesně vědom, jak vysoko mám laťku, kterou ještě zvládnu přeskočit.
Co s tím? V záloze se zdála být poslední možnost, totiž že poprosím některého více inteligentního spolužáka, aby mi příklad vyřešil, za což ho pozvu na jídlo a pivo. Ale nedalo mi to. Šel jsem na to přes grafiku, zkoušel jsem malovat různé grafy; volně, jak mě to napadlo. Nakonec jsem s úlevou zjistil, že můj graf zvládá jakýkoliv vstupní řetězec znaků podle zadání příkladu a vychrlí na výstupu ten správný, požadovaný. Z grafu jsem již snadno odvodil příslušná pravidla gramatiky. Přesto k zápočtu jsem šel s obavou. Po ruce jsem měl kromě pravidel gramatiky i svůj graf. Odborný asistent mi zadal na vstupu jakýsi řetězec a já měl na svých pravidlech ukázat, že výstup bude takový, jak se dle zadání požaduje. Na pravidla gramatiky jsem se vykašlal a vše jsem vysvětlil na grafu. Byl jsem pochválen, že jsem na to šel přes jakýsi (vyslovil jakési anglicky znějící jméno) automat. Jakýsi píšu proto, že v té době to anglické jméno jsem slyšel poprvé a vůbec jsem jej nepochytil, takže jsem místo odpovědi jenom něco zakoktal.
Na chodbě ukazuje jednomu velice inteligentnímu kolegovi můj graf, a povídám mu, že asistent mi řekl, že to je nějaký automat. Hned pohotově reaguje: „Jasné, to jsme měli v minulém semestru v logických systémech.“ Tak těm jsem moc nedal. V dálkovém studiu se ve škole celá látka nepřednášela ani zdaleka, většinu látky jsme si museli nastudovat sami. S automaty to bylo možná podobně nebo jsem v té době na přednášce nebyl kvůli časové vytíženosti v zaměstnání. Či tak nebo onak látku kolem automatů jsem zcela vypustil, věříce, že otázku z automatů si nevytáhnu. Ale nedalo mi to, hned doma jsme se do skript Logické systémy podíval a zjistil jsem, že je to docela zajímavá teorie. Látku jsem si hned doplnil a znám ji jakž takž dodnes. V praxi jsem ji využil pouze jednou. Bývalý kolega z práce, programátor, naklikal pomocí workflow (představte si něco, jako řízené a vyhodnocované toky dat) jakousi funkcionalitu, jenomže nefungovala zcela tak, jak jsme očekávali. Celou funkcionalitu jsem zachytil pomocou grafu automatu. Najednou bylo hezky vidět, kde je problém.
Vlastní zkouška z Gramatik a jazyků po zmíněném zápočtu moc slavně nedopadla, dostal jsem to za tři (podobně jako již ze zmíněných Logických systémů), což v té době byl poslední možný stupeň, aby člověk zkoušku vůbec měl, také se místo trojky říkalo "mám to". Studium jsem neflinkal, ale při dvoch malých dětech, vojenském povolání extrémně náročném na čas, častých 24 hodinových službách, jsem dálkové studium často časově nezvládal.
Ale vraťme se z vysoké školy na střední stupeň. Za nás jsme se nic kolem počítačů neučili. Dnes se tam kromě informatiky učí i něco málo o dvojkové soustavě, tedy o soustavě, v níž vystačíme s dvěma znaky, zvanými číslice. Jsou to číslice 0 a 1. Kupříkladu v elektrotechnice se často pracuje jenom s dvěma stavy: proud obvodem teče, nebo neteče; zařízení je zapnuto, nebo vypnuto; na výstupu je, nebo není signál apod. Dále se využívá v logice, kde obvykle 1 představuje pravdu, 0 nepravdu. V běžném životě počítáme jenom desítkově, ovšem dvojkovou soustavu používáme, ač si to obvykle ani neuvědomujeme i tam: miluje mě, nebo nemiluje; budu, nebo nebudu dědit; udělám, nebo neudělám zkoušku apod.
Vidíme, že výuka dvojkové soustavy své opodstatnění má. Učitelé při vysvětlování zmíněné látky vytrvale studentům či učňům vysvětlují, že principiálně se s dvojkovou soustavou pracuje stejně jako s desítkovou, jenom základ je jiný, u desítkové soustavy je základ číslo 10, u dvojkové číslo 2. Podobnost je dána tím, desítková i dvojková soustava jsou poziční soustavy, což znamená, že číslici na určité pozici musíme vynásobit příslušnou mocninou základu danou příslušnou pozicí číslice, abychom věděli, jakou kvantitativní hodnotu konkrétní číslice reprezentuje.
Uvažujme nejprve desítkovou soustavu, v které používáme deset znaků, zvaných číslice: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Pro větší názornost a konkrétnost budeme uvažovat číslo 373 v desítkové soustavě. Máme tam dvě číslice 3, ale každá reprezentuje zcela jinou kvantitativní hodnotu, což je dáno pozicí, na které se ta která číslice 3 nachází. Na poslední pozici znamená číslo 3, protože 100 je 1 a 3. 1 = 3, kdežto na počáteční pozici číslo 300, protože 102 je 100 a 3. 100 = 300. A samotnou kvantitativní hodnotu celého čísla dostaneme součtem: 3.100 + 7.101 + 3.102. Pokud jde o jednu ze základních aritmetických operací, sčítání, platí pravidlo, že lze sčítat pouze číslice na stejné pozici. Jediná komplikace vzniká, když součet číslic na stejné pozici je roven číslu 10 nebo je větší než 10. V tomto případě musíme pamatovat na přenos do vyššího řádu. Kupříkladu když sečteme na stejné – např. poslední, jednotkové – pozici číslice 9 a 8, dostaneme číslo 17, číslici 7 zapíšeme na jednotkovou pozici, ale nesmím zapomenout na to, co zbylo do 17, tedy na číslo 10, přesněji 1 desítku, kterou musíme připočíst k počtu desítek na desítkové pozici. Obecně mluvíme o přenosu do vyššího řádu. Příklad výpočtu součtu dvou desítkových čísel při zápisu pod sebou pro jeho elementárnost vynecháme.
Jelikož jsme si řekli, že s dvojkovou soustavou se pracuje stejně jako s desítkovou, povídání z předchozího odstavce teď téměř zopakujeme. V té používáme pouze dva znaky, zvané číslice: 0 a 1. Uvažujme pro větší názornost a konkrétnost číslo 1101 v dvojkové soustavě. Máme tam tři číslice 1, ale každá reprezentuje zcela jinou kvantitativní hodnotu, což je dáno pozicí, na které se ta která číslice 1 nachází. Ta na poslední pozici znamená číslo 1, protože 1.20 = 1, na třetí pozici od konce kvantitativně reprezentuje číslo 4, protože 1.22 = 4 a na čtvrté pozici od konce kvantitativně číslo 8, protože 1. 23 = 8. Samotnou hodnotu čísla dostaneme výpočtem součtu: 1.20 + 0.21 + 1.22 + 1.23, což je 13. Pokud jde o jednu ze základních aritmetických operací, sčítání, platí, že lze sčítat pouze číslice na stejné pozici. Jediná komplikace vzniká, když součet číslic na stejné pozici je roven nebo větší než 1. V tom případě musíme pamatovat na přenos do vyššího řádu. Kupříkladu když sečteme na stejné, např. poslední jednotkové pozici, číslice 1 a 1, dostaneme dvojkově číslo 10 (což je desítkově 2), číslici 0 zapíšeme na jednotkovou pozici, ale nesmím zapomenout na zbývající číslo, tedy 2, přesněji 1 dvojku, kterou musíme připočíst k počtu dvojek na dvojkové pozici (21 = 2). Malý příklad pro větší názornost: sečteme si pod sebou dvě dvojková čísla: 1111 (desítkově 15) a 1110 (desítkově 14). Dostaneme 11101 (desítkově 29). Jak jsme počítali? 0 + 1 =1; 1 + 1 = 10, nulu zapíšeme, 1 si zapamatujeme pro přenos do vyššího řádu; 1 + 1 = 10 + 1 (přenos) = 11, 1 zapíšeme, 1 si zapamatujeme pro přenos do vyššího řádu; 1 + 1 = 10 + 1 (přenos) = 11, 1 zapíšeme, 1 si zapamatujeme a zapíšeme ji do nejvyššího řádu.
Pochopitelně tohle povídání je zcela elementární a podobných výkladů je na Internetu více než dost. Můj důvod je jako obvykle jiný. Což tak na naše dvojkové sčítání jít přes automat, o němž jsem se již zmínil v úvodu! Díval jsem se na Internet, na výklad sčítání dvou dvojkových čísel přes automat jsem nenarazil. Ale určitě někde bude, přece nemůžu být jediný, koho by dvojkové sčítání napadlo takhle vyložit středoškolákům nebo učňům! Nebojte se výklad bude zcela lapidární a pochopí jej i babička ze zapadlé vesnice. Občas sice použijeme formálnější zápis, ale předtím si neformálně vše vysvětlíme. Každý formalismus má v sobě zcela přirozenou logičnost, jelikož jej vymysleli lidé.
Abychom se po dlouhém vyčerpávajícím prologu nějak rozběhli, na obrázku č. 1 (číslo obrázku zjistíte po najetí kurzoru myší na něj) je nakreslený ohodnocený orientovaný graf. Orientovaný je proto, že šipky vyznačují orientaci hran. Ohodnocený proto, že všechny hrany jsou ohodnoceny textem. Kolečka jsou stavy, v nichž se můžeme octnout. Veškerý text chápeme intuitivně tak, jak mu rozumíme v běžném jazyce. Abychom se z jednoho stavu dostali do jiného, musí se něco stát (nějaká událost). Jeden stav je výchozí, ten jsme vyznačili dvojitým orámováním. Koncový stav náš automat definovaný nemá, můžeme skončit všelijak. Podobné grafy se s oblibou používají v knihách, kde máme co činit s lidským myšlením a chováním.
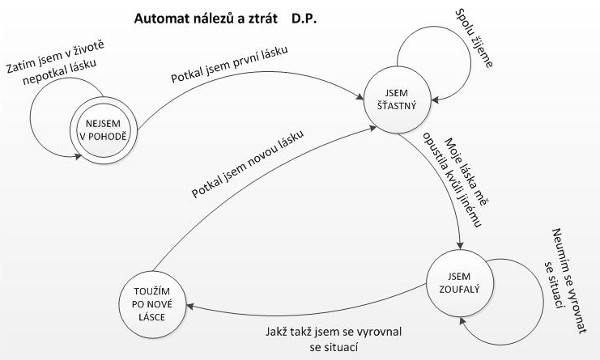
Náším cílem bude nakreslit podobný graf, bude to graf automatu, pomocí něhož sečteme dvě dvojková čísla bez přemýšlení, přesně jako cvičené opice. Jak budeme postupovat? Nejdříve si definujeme jeden speciální druh automatu, jeho logiku fungování zachytíme ve dvou tabulkách. Pak si přesněji definujeme orientovaný ohodnocený graf. Posléze si vysvětlíme postup, jak transformovat automat definovaný tabulkami na orientovaný ohodnocený graf. Pochopitelně nakonec si vše otestujeme na příkladu, zda automat v podobě grafu funguje tak, jak očekáváme.
V praxi se používají dva typy automatů: Mealyho a Mooreův (ten druhý se ještě někdy dělí na I. a II. druhu). Nám se více bude hodit Mealyho, ale jinak platí že Mealyho a Moorův automat jsou vzájemně ekvivalentní. Ekvivalenci automatů si nebudeme přesně definovat, ale zjednodušeně řečeno, když známe jeden typ automatu, umíme nadefinovat i ten druhý tak, aby oba dělaly to stejné. Pro vzájemné převody automatů známe formální postupy, tedy algoritmy.
Vstupy Mealyho automatu jsou tvořeny všemi možnými kombinacemi, které mohou vzniknout při součtu dvou dvojkových čísel: 00, 01, 10, 11. První číslice z dvojice patří prvnímu dvojkovému číslu, druhá druhému dvojkovému číslu. Možné výstupy jsou 0 a 1, protože pod stejnou pozici čísel, jejichž součet hledáme, můžeme zapsat pouze 0, nebo 1. Mealyho automat na začátku bude výždy ve výchozím stavu (je to na začátku jeho činnosti jeho aktuální stav), ten musíme přesně určit. V tomto stavu načte na vstupu aktuální data. Vstupy vyhodnotí a podle nich buď zůstane v aktuálním stavu, nebo se přepne do jiného stavu přičemž na výstup dodá data, která jsou definována aktuálním stavem a aktuálním vstupem. V novém aktuálním stavu (pokud zůstal ve výchozím stavu, je to jeho aktuální stav) stavu opět přijme na vstupu data a buď opět zůstane v aktuálním stavu, nebo se přepne do jiného stavu (ten se stane jeho novým aktuálním stavem) přičemž na výstup dodá data, která jsou definována původním aktuálním stavem a původním aktuálním vstupem. Činnost automatu bude pokračovat do té doby, dokud budou na vstupu nějaká data. Vlastní funkcionalita Mealyho automatu je určena dvěma funkcemi. Přechodová funkce nám určuje, do jakého stavu se automat přepne, případně nepřepne a zůstane v aktuálním stavu, poté co v určitém stavu přijal na vstupu aktuální data. Výstupní funkce nám zase určuje, jaké konkrétní výstupní hodnoty automat dodá na výstup poté, co v určitém aktuálním stavu přijal na vstupu aktuální data. Shrnuto: k jednoznačné defici Mealyho automat musíme znát 5 atributů: vstupy, stavy automatu, výstupy, přechodovou a výstupní funkci. Bez přesné formální definice se obejdeme. Na obrázku č. 2 je příklad Mealyho automatu, který umí sečíst dvě dvojková čísla. Při jeho definici jsme vystačili se dvěma stavy: X1 a X2.
Jak jsme se ke konkrétním hodnotám v tabulkách dopracovali? Ukážeme si vyplnění jednoho políčka v obou tabulkách, ostatní políčka si již lehce doplníte sami. V přechodové funkci jsme v stavu X1 (tedy musíme přičíst 1 k vyššímu řádu) a na vstupu máme 00. Do jakého stavu se automat přepne? Do stavu X2. Proč? No proto, že sice máme přenos z vyššího řádu, ale na vstupu máme 00, takže výstup bude: 0 + 0 = 0 + 1 z přenosu = 1. Tuto hodnotu zapíšeme do výstupní funkce do políčka, kde se křižuje X1 a 00 a můžeme přistoupit k zpracování další dvojice bez přenosu do vyššího řádu z pozice, kterou jsme právě zpracovali, což je typické pro stav X2.

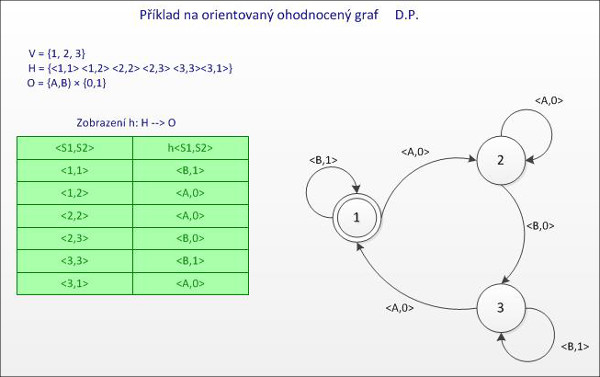
Nevýhodou tabulkového zápisu je jeho menší názornost. V dalším si vysvětlíme, jak lze Mealyho automat transformovat na orientovaný ohodnocený graf, který je obvykle názornější než tabulky. Na obrázku č. 3 je jakýsi ohodnocený orientovaný graf. Graf má vrcholy, má hrany, protože graf je orientovaný, musíme nějak vyznačit, v kterém vrcholu hrana začíná a v kterém končí. A protože graf je ohodnocený, musí být cosi nad každou hranou zapsáno, čemuž říkáme ohodnocení hrany. Nám bude vyhovovat, aby ohodnocení mělo dvě podmnožiny znaků (určitě tušíme, že v grafu automatu budou vyjadřovat vstupy a výstupy). Náš graf tedy bude mít celkem 4 atributy: vrcholy (V), orientované hrany (H), množinu všech možných uspořádaných dvojic vstupů a výstupů (O) a zobrazení h, které definuje jaké ohodnocení se má té které orientované hraně přiřadit. To, co zobrazený graf vyjadřuje, nás vůbec nezajímá, jde nám pouze o pochopení formálního zápisu a vyjádření grafické podoby. Náš graf na prvním obrázku byl jednodušší, ohodnocení hran vyjadřovalo pouze vstupy (podněty, události), které vyvolaly přechod do jiného stavu. Ohodnocení tohoto grafu má vstupy i výstupy. Vstupy používají znaky A, B, výstupy znaky 0, 1.
A stojíme před závěrečným krokem. Chceme Mealyho automat definovaný pomocí přechodové a výstupní funkce převést na graf. Formální postup popsaný na obrázku č. 4 vypadá docela složitě. Zkusme ale uvažovat logicky. Určitě vrcholy grafu budou stavy automatu. Jeden ze stavů bude výchozí, ten v grafu nějak vyznačíme, např. dvěma soustřednými kružnicemi. Orientovaných hran budeme mít pouze tolik, kolik je v přechodové funkcí přechodů ze stavů v levém sloupci do různých stavů v dalších sloupcích. Ohodnocení hran bude dáno všemi možnými kombinacemi vstupů a výstupů. Nejtěžším krokem bude přiřazení ohodnocení hranám. K tomu se budeme muset dívat do přechodové i výstupní funkce. Nejprve se podíváme do tabulky přechodvé funkce, zvolíme si konkrétní přechod z jednoho vstupního stavu (je zapsán v prvním sloupci) do druhého, přičemž si všimněme v hlavičce tabulky při jakém vstupu se tento přechod uskuteční. V tabulce výstupní funkce pro vstupní stav (z přechodové tabulky) a stejný vstup jaký byl v tabulce přechodvé funkce zjistíme výstup. Opět příklad. V tabulce přechodové funkce se v případě vstupního stavu X1 a vstupu 00 přepne automat do stavu X2. V tabulce výstupní funkce najdeme pro X1 a vstup 00 výstupní hodnotu 1. To znamená, že v grafu bude zakreslen přechod z X1 do X2 s ohodnocením <00,1>. A tak postupujeme dokud nevyčerpáme všechny přechody z jednodho stavu do druhého v tabulce přechodové funkce.
Na obrázku č. 4 vidíte Mealyho automat pro součet dvou dvojkových čísel v podobě grafu. Řekl bych, že je názornější než vyjádření pomocí tabulek přechodové a výstupní funkce.
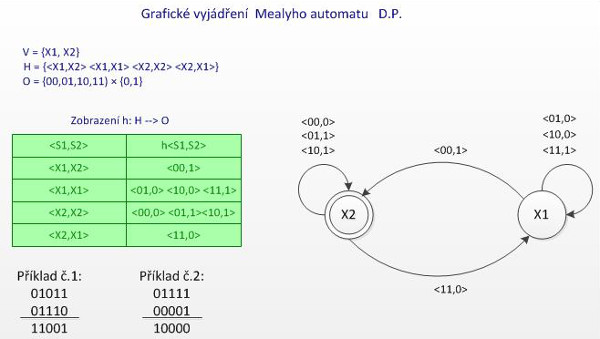
Sluší se náš automat otestovat na konkrétním příkladu. Teď již nemusíme znát žádná pravidla pro součet dvou dvojkových čísel, náš postup bude zcela mechanický. Máme sečíst dvě dvojková čísla: 1011 a 1110. Protože nevíme, zda se nakonec neuplatní i přenos z nejvyššího řádu těchto čísel do nejvyššího řádu výsledku, čísla si přepíšeme formálně tak, že před nejvyšší řád obou čísel napíšeme nulu: 01011 a 01110. A spustíme automat. Začneme ve výchozím stavu X2. Na vstupu máme 10, vidíme že výstup je 1, přičemž zůstáváme v stave X2. Další vstup je 11, automat nám naviguje pro tento vstup přechod ze stavu X2 do stavu X1, přičemž výstup je 0. Další kroky již nechám na vás, i kontrolu, že vše dopadlo dle očekávání, tedy že 11 + 14 = 25. Zkuste si ještě sečíst 1111 a 1. Nezapomeňte obě čísla automatu předpřipravit do vhodného tvaru: 01111 a 00001. No a to je málem vše.
Pokud vás automaty zaujaly, doporučuji k přečtení příslušnou kapitolu ze skript: RNDr. Jaroslav Janáček, CSc.: Teorie systémů, 1981, ALFA, Bratislava, Dočasná vysokoškolská učebnice, Vysoká škola dopravy a spojov Žilina. Skriptum je napsáno svěže a najdete zde i přesné formální definice objektů s nimiž zde pracujeme spíš na intuitivní úrovni. Několik málo označení z těch, co v textu používám, jsem převzal rovněž z tohoto titulu. Jelikož jinou knihu, v níž se pojednává o automatech, nemám, proto ani nevím, zda tohle označení je v souladu s dnešním úzusem. Ovšem označení je sekundární, důležitá je logika fungování.
V Brně mezi vánočním a novoročním svátkem Léta Páně 2016. Dopsáno na Silvestra těsně před půlnocí. Publikováno 2. ledna 2017.