Jena, koule, hádanka
Dušan Polanský
Starší dcera s rodinou strávila letošní Velikonoce v Německu poblíž Výmaru na pozvání své dlouholeté kamarádky a kolegyně ze studií. Při návratu domů se cestou stavili i v Jeně. Jena je střediskem sklářského, strojírenského (hlavně optické přístroje) a farmaceutického průmyslu. No a z Jeny mi poslala tuhle fotografii s prostým textem: Hádanka. Co to je?

Poslala mi ji proto, že ví, že k fyzice nemám negativní vztah, tím ale netvrdím, že mám pozitivní, jednoduše ji respektuji jako opravdovou vědu, v níž nestačí si vymyslet sebekrásnější teorii, leč aby byla uznána, musí být ověřena praktickými pokusy. Holt, není to filozofie. Na obrázku mě okamžitě upoutal vzoreček. Bylo jasné, že když ve vzorci vystupuje řecké písmeno lambda (λ), což, jak je známo, je ve fyzice časté označení pro vlnovou délku elektromagnetického záření (světlo je elektromagnetické záření), že vzorec souvisí s vlnovou optikou; dodám, že optiku máme ještě geometrickou a kvantovou. Písmenko d mi připomnělo mřížkovou konstanta, která souvisí s difrakční mřížkou, což je jakési zařízení, které má v sobě veliké množství štěrbin (vrypů). To moc si představte u běžných mřížek např. 100 vrypů na 1 mm, ale jsou i mřížky, které mají 2000 vrypů na 1 mm. Difrakční proto, že se pomocí difrakční mřížky studují difrakční jevy. Difrakce je jev, který bych laicky vysvětlil tak, že světlo vidí i za roh budovy. Trochu explicitněji: když světlo dopadá na překážku s malým otvorem, jehož rozměry jsou srovnatelné s vlnovou délkou dopadajícího světla, tak část vlny se za otvorem rozšíří i za neprůhlednou část překážky, což je to moje vidění za roh. A tušil jsem, že vzorec bude nějak souviset s mikroskopem. A tady jsem se svými znalostmi skončil.
Nejprve jsem si řekl, že by to chtělo schéma mikroskopu, aby bylo vidět jak vůbec tenhle optický přístroj funguje. Nějak se mi žádné schéma nepozdávalo, a tak jsem si nakreslil svoje. Všimněte si také vzorec pro výpočet zvětšení mikroskopu, 25 cm je konvenční zraková vzdálenost nebo vzdálenost zřetelného vidění, ovšem ne u důchodce, ale mladého člověka, který má cca 25 let.
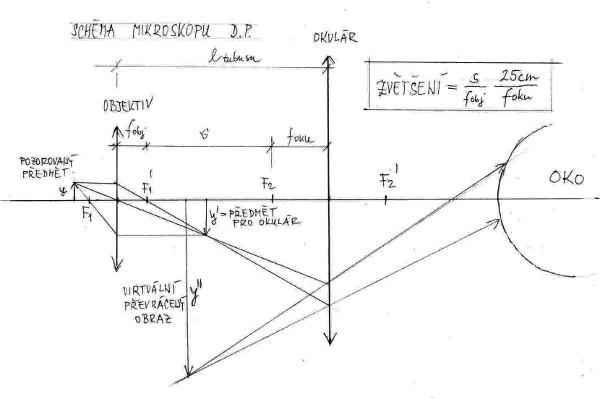
No a pak mě napadlo, že to chce vyřešit nějaký příklad. Sáhnul jsem po klasické sbírce příkladů z fyziky [2]. Našel jsem tam jeden jediný neřešený příklad na výpočet zvětšení mikroskoupu. Zadání je prosté: Máme spočíst zvětšení mikroskopu, když ohnisková vzdálenost okuláru je 20 mm, objektivu 5 mm a délka tubusu 12 cm. Do vzorce pro výpočet zvětšení potřebujeme znát velikost s, tzv. distanci (neboli optický interval mikroskopu), ta je: 120 - 5 -20 = 95 mm. Po dosazení do vzorce a po jednoduchém výpočtu dostaneme 237,5 násobné zvětšení. Výsledek sedí s výsledkem uvedeným v [2].
Ovšem horší to bylo se vzorcem na pomníku. Ale od čeho máme odbornou literaturu! Sáhnul jsem do své knihovny po titulu [1]. Lehce jsem v knize polistoval, a hle na stránkách 807 a 808 to bylo. Hádanka opravdu souvisí s optickým mikroskopem; ale opatrně, ne s elektronovým! Vzoreček na obrázku, jehož objevitelem je fyzik Ernst Abbe (1840–1905) nám říká, že ani optický mikroskop nemá nekonečnou rozlišitelnost (schopnost odlišit od sebe dva body), a že existuje jakási limitní vzdálenost mezi dvěma body, za níž již mikroskop ony dva body nedokáže coby jednotlivé entity rozeznat, tedy splynou mu v jeden bod. Tento problém je způsoben vlnovou povahou světla. Pokud budeme totiž vycházet z čistě geometrické teorie světla a nezohledníme jeho vlnovou povahu, mikroskop nemá žádnou limitní vzdálenost dvou bodů, za níž by je nedokázal rozeznat. Jenomže realita je realita. No a tuhle limitní vzdálenost můžeme lehce spočíst podle vzorečku na památníku. Vše jsem shrnul na dalším obrázku, a abych zvýraznil skutečnost, že vzdálenost d musí být větší, aby si mikroskop s rozlišením dvou bodů uměl rady, uvedl jsem ve vzorečku, že tahle vzdálenost musí být rovná nebo větší. Někdy se také místo schopnost říká mez, tedy rozlišovací mez optického mikroskopu.
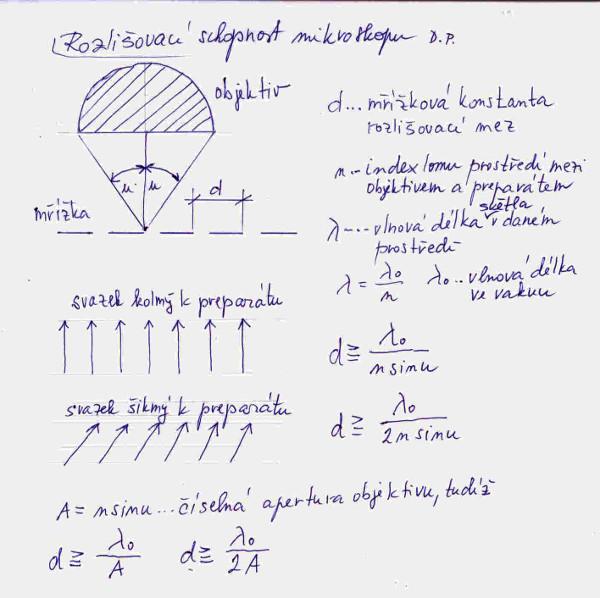
Ono vůbec fyzika si potrpí na fyzikální konstanty, za jejichž limitní hodnoty se jednoduše nedostanete, ať děláte co děláte. Asi nejznámější je rychlost světla. A co se již různí snílci vymysleli ptákovin, aby tuhle rychlost překonali, tedy alespoň v sci-fi románech či v tzv. popularizační literatuře, která často pod rouškou vědeckosti slouží k oblbnutí čtenářů. Nic naplat, je to tak a zůstane to tak navěky: světlo a informace se nemůže šířit větší rychlostí než je rychlost světla ve vakuu. Přiznám se, že ale jednu takovou konstantu nemám rád, jelikož její objevitel skončil velice smutně. Dnes fyzika ví, že prostor, ale také čas nejsou nekonečně dělitelné. Pokud jde o nejmenší oblast prostoru, jeho délka je daná určitým vzorečkem. Této délce se říká neprávem Planckova délka. Proč neprávem? Proto, že tuhle délku poprvé vyjádřil vzorcem v roce 1930 sovětský fyzik Matvej Petrovič Bronštejn (1906 – 1938). Jeho život skončil velmi smutně. 18. února 1938 byl zatčen Stalinovou policii, téhož dne odsouzen a téhož dne i popraven. V Stalinově impériu i hodnota génia byla nulová.
No a opět to chtělo vyřešit nějaký příklad. Opět jsem sáhnul po klasické sbírce příkladů z fyziky [2]. Našel jsem tam opět jeden jediný neřešený příklad s uvedením výsledku. Zde je původní zadání v slovenském jazyce.
Vypočítajte, aká je najmenšia vzdialenosť mezi dvoma čiarkami, ktoré při pozorování optickým mikroskopom môžeme rozoznať, keď pozorujeme v modrom svetle vlnovej dľžky λ= 450 nm a číselná apertúra objektívu A = 0,55! Určite, koľkokrát je táto vzdialenosť menšia než vzdialenosť, ktorú ešte rozozná voľné oko zo vzdialenosti l = 25 cm, keď vieme, že najmenší uhol, pod kterým ešte oko rozlišuje dve čiarky, alfa = 1´!
Přiznám se, že o té jedné sekundové minutě na vzdálenost 25 cm volným okem nejsem přesvědčen, ale ctím zadání. Dodejme, že při běžné intenzitě osvětlení je sítnice citlivá v oblasti elektromagnetického záření o vlnové délce od 380 nm do 760 nm, pomyslný střed je kolem 550 nm, což je žlutozelená barva, i proto je tak příjemné se dívat do zeleně lesů nebo rozkvetlé louky. No a tady je moje řešení. Nic složitého, tedy až na počítání s malými hodnotami. Víme si představit, že fotbalové hřiště je dlouhé cca 100 metrů, že do sousední vesnice to je 5 kilometrů atd. Leč představit si 1 μm (miliontinu metra) je těžší, kupříkladu jemný lidský vlas má průměr 100 μm, ale vryp na kompaktním disku má šířku pouze 0,5 μm! O nanometrech raději ani nemluvě!
![Řešení příkladu z [2].](../obrazky/mikroskop-3.jpg)
Při porovnání mého a autorského řešení mě potěšilo, že moje výsledky sedí s řešením autorů, tedy až na maličkost, mně vyšla hodnota 177, jim 178, ale to je vysvětlitelné zaokrouhlováním, jelikož se pracuje s malými hodnotami.
V literatuře se uvádí, že optický mikroskop je zařízení, které používáme k pozorování předmětů, které nejsme schopni spatřit pouhým okem (uvažuje se opět konvenční vzdálenost 25 cm), tj. předmětů, které mají velikost menší než 0,2 mm. Pokud chci ještě rozlišit volným okem na vzdálenost 25 cm dva body od sebe vzdálené 0,2 mm stačí se dívat pod cca úhlem 2°40´! Alespoň tak mi to vyšlo. Zkontrolujte mě!
U optického mikroskopu se uvádí rozlišovací schopnost od 0,2 mm do 0,2 μm. Pro rozeznání menších objektů musíme použít mikroskop elektronový, který rozliší objekty až do velikosti 0,1 nm (1 nm = 0,000 000 001 m). Dodejme, že se používají i skenovací mikroskopy. Běžně se používají skenovací tunelové mikroskopy pro plošné skenování, a velikým hitem současnosti je 3D laserový skenovací mikroskop, který umí naskenovat nejen plošné ale i prostorové struktury.

V každém případě mikroskop je přístroj s nenahraditelným významem pro veškeré přírodní vědy, nemluvě už vůbec o zdravotnictví. Ne náhodou byly za výzkum v oblasti mikroskopů uděleny i Nobelovy ceny. V roce 1953 ji obdržel Frits Zernike (1888-1966) zejména za vynález mikroskopu založeném na fázovém kontrastu; v roce 1986 Ernst Ruska (1906-1988) za vynález elektronového mikroskopu a Gerd Binnig (1947) a Heinrich Rohrer (1933-2013) za vynález řádkovacího tunelového mikroskopu.
Svět optiky, a tudíž i mikroskopů je víc než zajímavý. Pokud vás tento svět zaujal neváhejte, valte do obchodu a kupte si kvalitní optický mikroskop! A pokud se octnete v Jeně, nezapomeňte se dát vyfotit u výše vyfocené koule, tedy asi to bude oko, a symbolika těch čárek by mohla být snad podobná čárkám z námi řešeného příkladu. Ale teď trochu hádám. No a pokud vám ještě zbyde kousek času, tak si klidně s Ernsem Abbem popovídejte, a nemusí to být jenom o mikroskopu. Fyzici jsou totiž také jenom lidé s běžnými radostmi i starostmi.
Seznam použité literatury: [1] Horák, Z. Krupka, F.: Fyzika, Svazek 2, SNTL ALFA, Praha 1976. [2]Hajko, V. a kolektív: Fyzika v príkladoch, ALFA, Bratislava 1983
.V Brně 15. dubna 2023.