Mince a matematická indukce
Dušan Polanský
Důkaz matematickou indukcí je středoškolská látka, ale bere se i na výšce. Je to taková malá matematická rafinovanost, ačkoliv pochopení techniky tohoto důkazu je vcelku jednoduché. Často tento typ důkazu matematici používají k tomu, aby utajili intuitivní postup, jakým kápli na nějakou matematickou zákonitost, jednoduše nám nechtějí prozradit, jak jejich intuice zapracovala. No a na co přišli obvykle intuicí, dokážou následně čistě formálně právě matematickou indukcí. Kupříkladu dojít na binomickou větu není až tak jednoduché, ale její důkaz matematickou indukcí není až tak těžký. Na ukázku jsem ho zařadil do dodatku k tomuto textu. Pokud se vám zdá těžký, nic se neděje, pro pochopení řešeného problému je zcela irelevantní.
O co nám půjde. Budeme se snažit vyřešit průměrně složitý matematický hlavolam. V průběhu hledání řešení našeho problému se nám na intuitivní úrovni podaří vytušit určitou zákonitost. Ovšem zatím si máme právo jenom myslet, že jsme na něco přišli. Aby se z naší domněnky stala pravda, musíme náš intuitivní předpoklad dokázat. A k důkazu použijeme matematickou indukci a to trochu netradičně. Proč? No proto, aby to bylo patřičně netriviální. Triviálních důkazů matematickou indukcí najdete na internetu habaděj.
Čistě zbytečná technická poznámka. V textu jsou i dva obrázky s vývojovými diagramy. K jejich nakreslení jsem použil free program GIMP, který se k tomuto účelu vůbec nehodí, jelikož je to bitmapový grafický editor, viz kostrbatost kresby. Vývojové diagramy umí hezky i Word, např. 2016, ovšem neumí nakreslený diagram vyexportovat do obrázku příslušného formátu. Pokud je vývoják menší, můžete jej nasnímat do obrázku např. pomocí programu Gawin PrintScreen. Dokud jsem ještě byl aktivně zapojen do pracovního procesu, používal jsem v práci produkt Visio od Microsoftu, který opravdu vřele doporučuji. Sice není až tak levný, ale umí opravdu spoustu různých typů diagramů, plánů apod. Ale již dost žvanění, dáme se do zábavy.
Naše ůloha: máme libovolný, ale určitý počet mincí mezi nimi je jedna jediná falešná, pro konkrétnost je lehčí než standardní mince. Máme určit minimální maximum počtu vážení na rovnoramenných vahách (někdy se jim říká také miskové – misky jsou dvě) potřebných k určení falešné mince. Ale může se stát, že v určitých případech v určitém intervalu mincí, kde bude minimální maximum n, nebudeme potřebovat ani n vážení, ale méně.
Zkusme jak nám to půjde. V případě 1 mince neumíme rozhodnout, zda je falešná, jelikož nemáme její hmotnost s čím porovnat.
V případě 2 mincí vystačíme s 1 vážením. Na každou misku vah dáme 1 minci. Falešná mince bude v misce, která vystoupá výš.
V případě 3 mincí stále vystačíme s 1 vážením. Na každou misku vah dáme 1 minci a zbývající minci odložíme bokem. Pokud některá miska vystoupá výš, je v ní falešná mince. Pokud zůstanou misky v rovnováze, mince odložená bokem je falešná.
V případě 4 mincí budeme muset vážit 2 krát. Na každou misku položíme 2 mince. V misce, která vystoupá výš je falešná mince. K jejímu zjištění budeme potřebovat další vážení.
A jak to bude vypadat např. v případě 9 mincí? Na misky vah dáme po 3 mincích, 3 zbývající mince odložíme bokem. Pokud budou misky vah v rovnováze, falešná mince se nachází ve třech odložených mincích. Ale již víme, že v případě 3 mincí vystačíme s jedním vážením. Podobně tomu bude, pokud jedna miska vah při prvním vážení vystoupá výš. Takže celkem budeme vážit 2 krát.
A co případ 10 mincí? Na každou misku položíme 5 mincí. V misce, která vystoupá výš je falešná mince. Na každou misku dáme po 2 mincích. Jednu minci odložíme bokem. Jestli jsou misky v rovnováze, tak falešná mince je odložená bokem. V tomto případě vystačíme s 2 váženími. Pokud jedna miska vystoupá výš, musíme dalším vážením zjistit, která je falešná. Takže minimální maximum počtu vážení je 3.
Jak bude probíhat vážení v případě 27 mincí jsem zachytil na vývojovém diagramu. Ve vývojovém diagramu rozhodovací blok je ekvivalentem jednoho vážení. Kolik rozhodovacích bloků, tolik vážení. Vážili jsme celkem 3 krát.
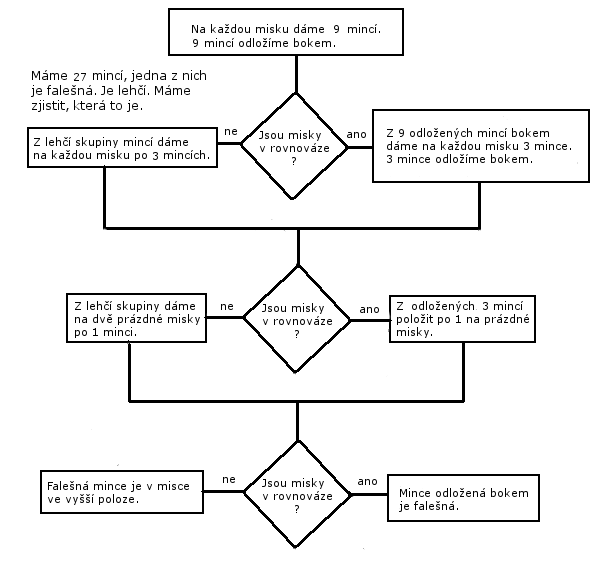
Jak to bude vypadat v případě 28 mincí? Na každou misku položíme 14 mincí. V misce, která vystoupá výš je falešná mince. Těchto 14 mincí rozdělíme opět na polovinu. V misce, která vystoupá výš je falešná mince. 7 mincí v lehčí misce doplníme 2 libovolnými mincemi z druhé misky, čímž budeme mít 9 mincí. Pro těchto 9 mincí použijeme postup pro 9 mincí, což jsou 2 vážení. Ale můžeme to udělat ještě jinak. Na každou misku položíme 14 mincí. V misce, která vystoupá výš je falešná mince. Počet mincí v této misce doplníme na 21, tedy z druhé misky přidáme 7 mincí. Na 21 mincí použijeme již uvedený postup. Tak či onak museli jsme vážit 4 krát.
Jak to bude vypadat v případě 80 mincí mincí je zachyceno na dalším vývojovém diagramu. Celkem jsme vážili 4 krát.
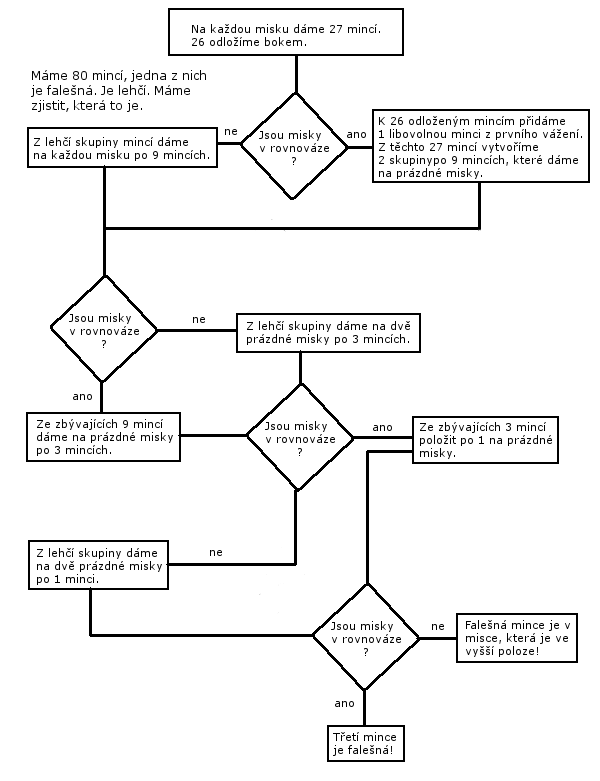
A co v případě 81 mincí? Na misky dáme po 27 mincích, zbývajících 27 odložíme bokem. Pokud jsou misky v rovnováze, tak falešná mince bude v odložených 27 mincích bokem. Pro zjištění, která to je, aplikujeme postup s 27 mincemi. Pokud misky nejsou v rovnováze, falešná mince bude v misce, která vystoupá výš. Ale těchto mincí je opět 27, takže opět aplikujeme postup pro 27 mincí. Tedy celkem budeme vážit 4 krát.
K čemu jsme se zatím intuitivně dopracovali, je zachyceno v následující tabulce:
| Počet mincí | 2 až 3 | 4 až 9 | 10 až 27 | 28 až 81 |
|---|---|---|---|---|
| Počet vážení | 1 | 2 | 3 | 4 |
Teď se soustřeďme na počty mincí, u kterých lze falešnou minci zjistit stejným počtem vážení. Sledujte pozorně tabulku. Číslo 2 lze zapsat jako 30 + 1, číslo 3 jako 31. Číslo 10 jako 32 + 1, číslo 27 jako 33. Číslo 28 jako 33 + 1, číslo 81 jako 34. A co je zajímavé: mocněnec čísla 3 u horní hranice intervalu, v něž lze falešnou minci určit stejným počtem vážení, je současně počtem vážení v příslušném intervalu. Náhoda, nebo zákonitost? To zatím nevíme, ale přesto si jenom nesměle dovolíme vyslovit určité tvrzení (domněnku, hypotézu).
Jestli máme m mincí a jedna z nich je falešná, za předpokladu že 3 n-1 + 1 <= m <= 3n, tak k určení falešné mince bychom měli vystačit maximálně s n počtem vážení.
Aby se z domněnky stal matematický fakt, tedy věta, je potřeba domněnku dokázat. A právě k tomu použijeme techniku důkazu zvanou matematická indukce. Pokud se nám to povede, odhalili jsem zákonitost pro libovolný počet mincí. Pak můžeme kupříkladu tvrdit, že jelikož 34 + 1 <= m <= 35, tak pro interval od 82 po 243 mincí k určení falešné mince budeme potřebovat maximálně 5 vážení.
Než se do důkazu dáme, připomeňme si princip důkazu matematickou indukcí. Dané tvrzení v přirozených číslech se dokazuje ve dvou krocích. První krok spočívá v prostém dosazení n = 1 a v jednoduchém ověření, že dokazované tvrzení pro tento případ platí. V druhém, indukčním, kroku, je snaha dokázat, že pokud dokazované tvrzení platí pro n = k, pak platí i pro n = k + 1. Z těchto dvou kroků implikujeme, že naše tvrzení platí pro všechna přirozená čísla, potažmo pro všechna přirozená čísla některým přirozeným číslem počítaje, první krok totiž nemusí vždy být n = 1.
Pokud dokazované tvrzení označíme P(n), kde n je přirozené číslo, můžeme matematickou indukci popsat i stručněji: jestliže P(1) je pravdivé, a pokud P(k) implikuje P(k+1) pro všechna přirozená čísla, pak P(n) je pravdivé pro všechna přirozená čísla. Na internetu a v řadě učebnic lze najít řadu vyřešených příkladu na důkaz matematickou indukci. Trochu složitější příklad je uveden na konci textu v dodatku.
Ovšem náš důkaz matematickou indukcí nebude zase až tak jednoduchý, kdyby byl, tak bych tento text nepsal. Když si pozorně promyslíme, jak jsme u různých počtů mincí postupovali při odhalování falešné mince, zjistíme, že jsme vlastně používali tři postupy. A pro každý postup budeme teď muset matematickou indukcí dokázat (potažmo nedokázat) pravdivost našeho zatím intuitivního tvrzení.
Zmínil jsem tři postupy. Které to jsou?
První postup použijeme, když počet mincí lze zapsat jako m = 3k+1, kupříkladu m = 3.32 = 27, viz vývojový diagram pro m = 27. Podobný postup bychom použili např. i pro 81, jelikož m = 3.33 = 81.
Druhý postup jsme použili, když počet mincí nebyl mocninou tří, ale v případě rovnováhy v prvním vážení jsme počet odložených mincí doplnili do mocniny tří, viz kupříkladu vývojový diagram pro m = 80. Počet mincí pro doplnění (označme jej r) leží v intervalu 0 <= r <= 3k. V případě 80 mincí jsem doplnili pouze 1 minci. Kupříkladu pro m = 70, bychom bokem odložili 16 mincí (70 - 54) a do počtu 27 bychom doplňovali 11 mincí. Obecně tento postup použijeme pro m = 2.3k + r, kde 0 <= r <= 3k.
Třetí postup jsme použili pro m = 28. Pokud by m bylo liché, např. m = 47 postup by byl velice podobný: lichou minci bychom odložili bokem a zbytek rozdělili na dvě poloviny, pokud by při prvním vážení byly v rovnováze, je mince odložená bokem falešná, pokud by nebyly v rovnováze, použijeme postup obdobný pro m= 28. Obecně tento postup použijeme pro 3k < m < 2.3k.
Pro větší konkrétnost si představme, že se pobybujeme v intervalu 28 <= m <= 81, viz tabulku. První postup bychom použili pouze pro m = 81, druhý pro 54 <= m <= 80 a třetí pro 28 <= m <= 53. Doporučuji si tuhle skutečnost řádně ujasnit, jinak se v důkazu ztratíte. A teď se konečně můžeme dát do důkazu.
I.Začneme s n = 1. Je zřejmé, že s jedním vážením vystačíme pouze pro m = 2 a m = 3.
II.Teď budeme předpokládat, že naše tvrzení je pravdivé pro libovolné p <= k, tedy že, pokud počet mincí leží v intervalu 3p - 1 + 1 < m < 3p, tak bychom měli vystačit s počtem vážení n = p. Z tohoto předpokladu se pokusíme dokázat, že pokud počet mincí leží v intervalu 3k + 1 < m < 3k + 1, tak si vystačíme s počtem vážení n = k + 1. Opět pro větší konkrétnost si můžeme předsatvit, že naše tvrzení platí pro počet mincí v intervalu 10 <= m <= 27, což je předpoklad, a na základě něho mám dokázat platnost pro počet mincí v intervalu 28 <= m <= 81.
V souladu s naší předchozí úvahou budeme v tomto kroku uvažovat tři případy: 1. m = 3k+1, 2. m = 2.3k + r, kde 0 <= r <= 3k, 3. 3k < m < 2.3k.
1. případ. Máme 3k + 1, tedy 3.3k mincí. Pro názornost si představme 81 mincí. Na misky dáme po 3k mincích. Zbývajících 3k odložíme bokem. Jesliže jsou misky v rovnováze, falešná mince je v mincích odložených bokem. K nalezení falešné mince z 3k mincí potřebujeme podle indukčního předpokladu k vážení, což spolu s prvním vážením dáva spolu k + 1 vážení. Jesliže nejsou misky v rovnováze, falešná mince je misce, která vystoupá výš. K nalezení falešné mince v této misce opět potřebujeme podle indukčního předpokladu k vážení, což spolu s prvním vážením dáva spolu k + 1 vážení.
2. případ. Nech je mincí m = 2.3k + r, kde 0 <= r <= 3k. Představme si kupříkladu 70 mincí. Na misky dáme po 3k mincí. Zbývající odložíme bokem, těch je r. V našem příkladu jsme na misky dali po 27 mincích a 16 jsme odložili bokem. Jesliže jsou misky v rovnováze, falešná mince je v mincích odložených bokem. K nalezení falešné mince doplníme mince odložené bokem z mincí v miskách do počtu 3k, tedy doplníme 3k - r, v našem příkladu 11 mincí. K nalezení falešné mince v takto vytvořené hromady potřebujeme podle indukčního předpokladu k vážení, což spolu s prvním vážením dáva spolu k + 1 vážení. Jesliže misky nejsou v rovnováze, falešná mince je v misce, která vystoupá výš. V této misce je 3k mincí. K nalezení falešné mince z této misky potřebujeme podle indukčního předpokladu k vážení, což spolu s prvním vážením dáva spolu k + 1 vážení.
3. případ. Nech je počet mincí v intervalu 3k < m < 2.3k. Mohou nastat dva případy: a) buď je m sudé číslo, tedy m = 2p, kde p < 3k, kupříkladu m = 40, b) m je liché, tedy m = 2p + 1, kde p < 3k, kupříkladu m = 47.
Případ a). Mincí je m = 2p. Mince rozdělíme na dvě poloviny po p mincí a vzájemně je zvážíme. V misce, která vystoupá výš je falešná mince. Počet mincí v misce, ketrá vystoupala výš, doplníme z mincí v druhé misce do 3k. K nalezení falešné mince z 3k mincí potřebujeme podle indukčního předpokladu k vážení, což spolu s prvním vážením dáva spolu k + 1 vážení.
Případ b). Mincí je m = 2p + 1. 1 minci dáme bokem. Zbývající mince rozdělíme na dvě poloviny a vzájemně je zvážíme. Pokud jsou misky v rovnováze, falešná mince je odložená bokem. Pokud nejsou, postupujeme podle případu a).
Tím je důkaz proveden.
Naším cílem nebylo jenom formálně dokázat nějaké tvrzení, které nám je pasívně sděleno, ale i na tohle tvrzení detailní analýzou problému dojít. O tom totiž v matematice především jde, tedy mělo by jít profesionálním matematikům, my laici jsem tu od toho, abychom výsledky matematiky aplikovali. V neposlední řadě doufám, že vám tento text pomohl hlouběji pochopit techniku důkazu matematickou indukcí.
V Brně 28. dubna 2020.
Doplněk: Formální důkaz binomické věty matematickou indukcí:
