Úlohy o nádobách a nerovnosti
Dušan Polanský
Zadumal jsem se, co v době silných omezení kvůli ataku SARS-CoV-2 dát z matematiky na papír, ono totiž tím, že žáci a studenti mají nedobrovolné prázdniny docela dost se snaží něčemu naučit či alespoň přiučit i na internetu. Pozoruji to i z toho, že u mých odborných článků z matematiky a fyziky dost narostla v těchto těžkých časech sledovanost. Nakonec jsem se schválně rozhodl pro docela neoblíbenou látku, pro nerovnosti. Pochopitelně chci se pokusit ukázat, že i nerovnosti mohou být zajímavé. Takže hurá na ně přes jeden typ hlavolamu!
Matematici si obecně docela potrpí na matematické hlavolamy, kterými trápí laiky, dokonce u toho někdy si i zamachrují. Nejsa matematik, tak si na hlavolamy nepotrpím a už vůbec nemachruji. Spíš se snažím laikovi coby křesťan něco srozumitelně vysvětlit, a hlavně ukázat, že obvykle za konkrétním hlavolamem je skryto obecnější řešení, kde konkrétní hlavolam figuruje jenom jako speciální případ.
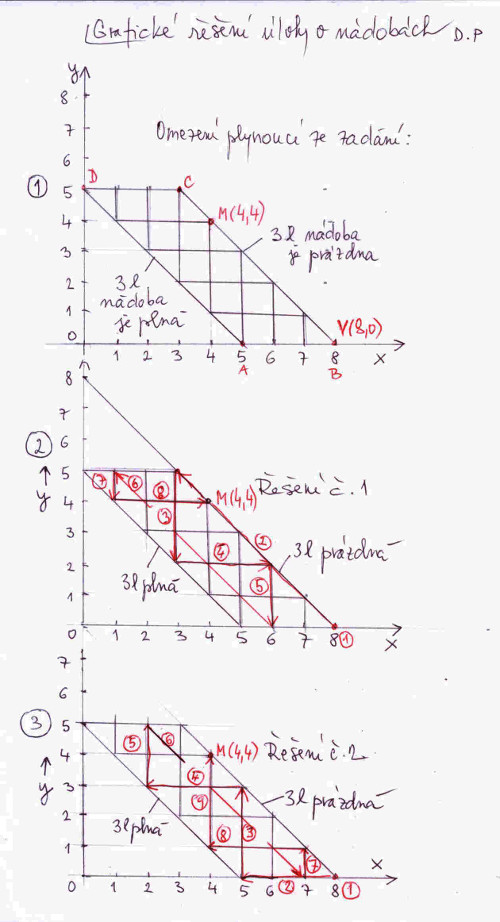
Docela velikou skupinou takových hlavolamů jsou úlohy o nádobách. Obvykle jsou k dispozici tři nádoby, každá o jiném objeme. Ve výchozím stavu je v některé nádobě určité množství vody, a zadání po nás chce, abychom vzájemným přeléváním vody mezi nádobami se dopracovali k stavu, kdy ve dvou konkrétních nádobách bude požadované množství vody. Abych byl konkrétnější, na obrázku č. 1. (číslo obrázku zjistíte po najetí kurzoru myši na obrázek) je zadaný i vyřešený (dokonce dvěma způsoby) takový jeden hlavolam. Zadání je poměrně jednoduché.
Máme tři nádoby, první má objem 8 l, druhá 5 l a třetí 3 l. V první nádobě je na počátku 8 litrů vody, přeléváním vody se máme dopracovat k stavu, kdy v první a druhé nádobě bude po 4 litrech vody. Kdo nemusí vodu, ať si doplní svůj oblíbený nápoj. Ale pozor 8 l je docela dost!
Pokud máte chuť a náladu můžete si zkusit úlohu vyřešit sami, pokud nemáte, na obrázku č. 1 vidíte dvě možná řešení. V tabulce každý řádek odpovídá určitému stavu všech nádob po přelití vody z jedné nádoby do druhé v předchozím řádku, tedy kromě výchozího stavu. Ovšem přiznám se na rovinu, že jsem se k těmto řešením dopracoval grafickou cestou. Jak, to si za chvíli podrobně ukážeme.

Intuitivně tušíme, že podobných úloh jenom s jinými objemy nádob může být nepřeberné množství. Kupříkladu k dispozici máme nádoby o objemu 12 l, 7 l a 5 l, první je plná, v konečném stavu má být v první a druhé nádobě po 6 litrech vody nebo další zadání: k dispozici máme nádoby o objemu 10 l, 7 l a 3 l, první je opět plná, a v konečném stavu má být v první a druhé nádobě po 5 litrech vody. Všimněme si, že u tohoto typu úloh jde o to, rozlít obsah vody v největší nádobě, která je plná, do dvou největších nádob tak, aby v každé byla polovina vody z největší nádoby. V knihách o matematických hlavolamech lze nalézt různé obměny těchto úloh. Kupříkladu, že v největší nádoba není plná, je tam pouze určité množství vody. Někdy se nepracuje s tekutinou, ale s váhovým množstvím nějaké látky např. v gramech. My v tomto povídání zůstaneme u typu úloh, jakou vidíme na obrázku č. 1. Ukážeme si, jak lze tento typ úlohy řešit graficky s využitím nerovností.
Pokud jde o požadované znalosti vystačíme se zcela elementární znalostí nerovností a analytické geometrie (stačí umět nakreslit z analytického zadání přímky obraz přímky v rovině x, y), tedy maximálně na úrovni prvního ročníku jakékoliv střední školy s maturitou.
Na obrázku č. 2 vidíme textové zadání úlohy převedeno do podoby soustavy nerovnic. Dobře si zafixujeme základní označení, viz bod č. 1: x je počet litrů v 8 l nádobě, y v 5 l, a počet litrů v třetí, nejmenší nádobě pak bude 8 – x – y litrů vody. Kupříkladu, když (3,5) chápeme jako uspořádanou dvojici, znamená to, že v 8 l nádobě jsou 3 litry vody, a v nádobě o objemu 5 l je 5 litrů vody, třetí nádoba je prázná, jelikož 8 - 3 - 5 = 0. S využitím tohoto označení jsou v bodě č. 2 formulovány 3 nerovnice, které v jiné podobě definují omezení na možné množství vody ve všech třech nádobách. Třetí nerovnost 0 ≤ 8 – x – y ≤ 3 upravíme do podoby 5 ≤ x + y ≤ 8. Tato nerovnost představuje dvě nerovnosti: 5 ≤ x + y a x + y ≤ 8. Tedy celkem máme čtyři nerovnosti, viz bod č. 3. Pokud vyjádříme tyto nerovnosti v grafické podobě dostaneme rovnoběžník ABCD, který vymezuje prostor řešení.

Ovšem ještě nejsme na konci. Teď si musíme ujasnit, jak máme postupovat při hledání řešení našeho hlavolamu. Nejprve si překreslíme náš rovnoběžník ABCD do podoby na obrázku č. 3, viz bod č. 1. Tečky jsou nahrazeny sítí protínajících se bodů v místě celočíselných souřadnic x a y. Zatím si nevšímejte nic z dalších popisů, k těm, ale i k dalším závěrům, se teprve dostaneme analýzou problému.
To, k čemu se analýzou postupně dopracujeme, si budeme vzestupně číslovat. U každého bodu pozorně sledujte obrázek pod bodem č. 1.
- Zadání je graficky jasné: máme se z bodu V(8,0), tedy že v největší nádobě je 8 l vody a v 5 l nádobě je 0 litrů dopracovat do bodu M(4,4), tedy že v těchto nádobách bude po 4 litrech vody.
- Vidíme, že případu, kdy 5 l nádoba je prázdná, tedy y-ová souřadnice je nulová, odpovídá úsečka AB, tedy možnosti 5, 6, 7 a 8 l. A naopak stavu, kdy je 5 l nádoba plná, tedy y-ová souřadnice má hodnotu 5, odpovídá úsečka DC, tedy možnosti 0, 1, 2 a 3 l, pouze tolik litrů vody může být v 8 l nádobě (pokud je 5 l nádoba plná).
- A jak je to s třetí nádobou? Kdy bud prázdná a kdy bude plná? Prázdná bude, pokud v zbývajících nádobách bude spolu 8 litrů vody. Této podmínce vyhovují pouze tyto množství vody: (8,0), (7,1), (6,2), (5,3), (4,4) a (3,5), což jsou body na přímce BC. Plná bude, pokud v zbývajících nádobách bude spolu 5 litrů vody. Této podmínce vyhovují pouze tyto množství vody: (5,0), (4,1), (3,2), (2,3), (1,4) a (0,5), což jsou body na přímce AD.
- Víme, že pokud přelíváme vodu z jedné nádoby do druhé, v třetí se množství vody nemění, to je dáno zadáním úlohy. Pokud se nemění množství vody v 8 l nádobě pohybujeme se po rovnoběžce s osou y. Pokud se nemění množství vody v 5 l nádobě pohybujeme se po rovnoběžce s osou x.
- A jak je to s třetí nádobou? Když se nemění množství vody v 3 l nádobě, tak suma x + y zůstává konstantní, tedy že se pohybujeme po přímce rovnoběžné s BC, kupříkladu, když je v třetí nádobě 1 l vody, tak suma x + y musí být 7 l. V kterých bodech může tato situace nastat? Jsou to body: (7,0), (6,1), (5,2), (4,3), (3,4) a (2,5). Když si tyto body spojíte, dostanete rovnoběžku s BC. Když je v třetí nádobě 2 l vody, tak suma x + y musí být 6 l. V kterých bodech táto situace může nastat? Jsou to body: (6,0), (5,1), (4,2), (3,3), (2,4) a (1,5). Když si tyto body spojíme, opět dostaneme opět rovnoběžku s BC. Speciálně když je 3 l nádoba plná pohybujeme se po přímce AD, a když prázdná po přímce BC, ale to již víme z bodu 3.
- Ještě se podívejme na body A, B, C a D. Nejprve čemu odpovídají body A a D. Už víme, že v bodě A je 3 l nádoba plná, takže musí platit x + y = 5, ale jelikož x = 5, tak musí být y = 0. V bodě D je 3 l nádoba plná, takže musí opět platit x + y = 5, ale jelikož y = 5, tak musí být x = 0. Teď čemu odpovídají body B a C. Už víme, že v bodě B je 3 l nádoba prázdna, takže musí platit x + y = 8, ale jelikož x = 8, tak musí být y = 0. V bodě C je 3 l nádoba opět prázdná, takže musí opět platit x + y = 8, ale jelikož y = 8, tak musí být x = 0. Vše je zřejmé i pouhým pohledem z obrázku. Závěrem k tomuto bodu můžeme říct, že jakákoliv orientovaná úsečka zachycující přechod z jednoho stavu obsahu třech nádob do stavu jiného, která leží na kterékoliv straně rovnoběžníku ABCD musí obsahovat jako koncový bod alespoň jeden z bodů A, B, C nebo D.
- Nakonec si je dobré uvědomit, třebaže to plyne již ze zadání, že pracujeme s celými litry vody, takže začátek a konec každé úsečky grafického řešení musí procházet body zadanými celými souřadnicemi. Tedy každý stav našeho systému je v každém kroku řešení plně popsán třemi celým čísly: x, y a 8 – x – y.
Na základě této analýzy můžeme definovat pravidla pro grafické řešení naší úlohy. Spojit bod V(8,0) s bodem M(4,4) lomenou čárou, jejíž vrcholy leží na obvodě rovnoběžníku ABCD, přičemž každý úsek této lomené čáry je rovnoběžný se souřadnými osami nebo s úsečkou BC. Přitom musíme dodržet pravidlo, že pokud úsek lomené čáry je podmnožinou obvodu ABCD, pak konec úseku musí obsahovat alespoň jeden vrchol rovnoběžníku ABCD. Dále pro počáteční a koncový bod každé úsečky znázorňující přechod z jednoho stavu do druhého platí omezení uvedené v bodě č. 7.
Na obrázku č. 3, bod č. 2 a č. 3. vidíte dvě geometrická řešení úlohy. Jejich přepis do tabulkové podoby byl již uveden je na obrázku č. 1.
Řešení nerovností nepatří k oblíbeným příkladům z matematiky, já je také nikdy neměl v lásce, ale myslím si, že někdy trochu přehnaně. Jenom to chce zvolit názorné příklady, kupříkladu jako je naše úloha o nádobách. Koneckonců čistě formální řešení čehokoliv bez konkrétního obsahu žáky a studenty od matematiky určitě více odstrašuje, než je k ní přitahuje. A vyhrožovat povinnou maturitou z matematiky to je už zcela o ničem.
V Brně 11. dubna 2020.