Nestrašte matematikou!
Dušan Polanský
Nedávno jsem sledoval slovenské televizní „Správy“, které začínají v 19,00 hod., a tam jsem se dozvěděl, že na Slovensku od roku 2027 bude pro nově začínající studenty na středních školách s maturitou povinná zkouška z matematiky, takže první maturanti budou skládat zkoušku z matematiky v roce 2031. Kdoví jak to nakonec ještě dopadne, znáte to, zákony se mění stále. A mezi námi, politiků co absolvovali vysokoškolskou matematiku nebude určitě moc, spíš pramálo. Takže politici rozhodují o něčem, co mají jenom z doslechu.
Když už se bavíme o matematice
Matematiku mám docela v oblibě, ale ne zas až tak veliké, abych byl zastáncem povinné maturitní zkoušky z matematiky. Když se budete chtít stát lékařem, je pro vás důležitější znalost angličtiny (kvůli domluvě s cizím pacientem), latiny (kvůli lékařskému názvosloví) a chemie či biologie, nebo matematiky? Když někdo studuje např. stavební průmyslovku (nebo jak se takové škole dnes říká), asi by nebylo správné, kdyby se mohl vyhnout maturitě z odborných předmětů, protože to by nám domy pak časem mohly začít padat na hlavu, což jistě nechceme. A nakonec v odborných předmětech matematika se používá. Vědci se shodují, že 21 století je a bude stoletím chemie, technologií a biologie, potažmo biochemie, tak proč není na gymnáziu povinná maturita např. z chemie či biologie?
Pochopitelně těm, co chtějí studovat na vysoké škole technické či na univerzitě nebo pedagogické fakultě matematiku, fyziku, chemii apod. vřele doporučuji vybrat si matematiku coby povinný maturitní předmět, jelikož bez kvalitního a pevného základu vyšší partie matematiky se zvládají těžko. Ale proč by měli mít matematiku povinnou všichni? Odpověď neznám. Matematici s oblibou uvádí, že učí logickému myšlení. Myslíte si, že když např. řemeslník má něco složitějšího zrealizovat, nemusí si úkol logicky ujasnit? Že stačí na to vlítnout?! To si totiž obvykle myslí hlavně ti, pro které je slovo řemeslo cizí a často i odpudivé slovo. Často to platí právě pro různé pseudointelektuály, kteří rozumí všemu a vlastně ničemu, ale často o mnohém rozhodují. A ani o matematicích nelze říct, že by to velicí milovníci praktických aplikací jejich vědy, spíš se utíkají k teoretickým úvahám. Ono totiž v praxi je vše o hodně složitější než v teorii.
Teď konečně něco z matematiky
Ale trochu jsem teď ujel od toho, kvůli čemu jsem tenhle článek začal psát. Je určen i pro středoškoláky, který matematiku až tak v lásce nemají. Chci jim ukázat krůček po krůčku, že třebaže nějaký výpočet vypadá málem hrůzně a vysoce intelektuálně, není finálně vůbec tak hrozný a hlavně, že dosažený výsledek nakonec člověka tak trochu potěší i intelektuálně.
Co budeme chtít spočíst je uvedeno v textu níže. Vypadá to divoce? Klídek, v pohodě to spolu zmákneme. Ovšem nejprve si k výpočtům musíme připravit matematický aparát. Tohle naše zadání jsem napsal v LaTeXu, což je systém pro sazbu písma, žádná novinka, už nějaký rok má. Obsahuje funkcionalitu určenou pro tvorbu technické a vědecké dokumentace. LaTeX je de facto standardem pro komunikaci a publikování vědeckých dokumentů. No a pak jsem text vygeneroval do formátu pdf, z něhož jsem vytvořil obrázek, na který se koukáte. Ovšem další výpočty jsem již napsal rukou. Přepsat do LaTexu se mi je již nechtělo. Ale doporučuji, vám mladým, LaTex se naučit.

Začněme obrázkem č. 1; číslo obrázku zjistíte po najetí kurzoru myši na příslušný obrázek. V obrázku není nic nového, co byste neznali ze střední školy. V bodě č. 1 je vysvětlena běžná a často používaná konvence pro sumaci a součin. V bodě č. 2 je definován kombinační koeficient. V bodě č. 3 je příklad na procvičení používání sumační konvence.

Na obrázku č. 2 bude uvedeno to, co bude pro nás nejdůležitější, totiž zobecnění binomické věty (viz první polovinu obrázku), jak ji znáte ze střední školy, na nekonečnou binomickou řadu, která se sice bere až na vysoké škole, ale v pohodě, zvládneme to. Abychom tuhle řadu mohli definovat, v bodě č. 1 je uvedeno zobecnění kombinačního koeficientu i pro reálné číslo alfa. V bodě č. 2 je uveden vzorec pro výpočet nekonečně binomické řady. Důležité si je uvědomit, že platí pouze pro |x| < 1. Je to sice silné omezení, ale nám při výpočtech z teorie relativity nebude vůbec vadit. Právě naopak! V bodě č. 3 je uveden výpočet kombinačního koeficientu – 1 nad n, který se v praxi občas vyskytuje, my ho použijeme v jednom nedůležitém příkladě.

Pro nás budou nejdůležitější kombinační koeficienty pro alfa = −1/2. Výpočet několika prvních kombinačních koeficientů je na obrázku č. 3. V druhé polovině obrázku je několik příkladů na výpočet nekonečné binomické řady. Nám se bude za chvíli velice hodit příklad s velikou modrou tečkou! Jako poslední je uveden příklad s koeficientem alfa = −1, v němž jsem využili vzorec z příkladu č. 3 na obrázku č. 2.
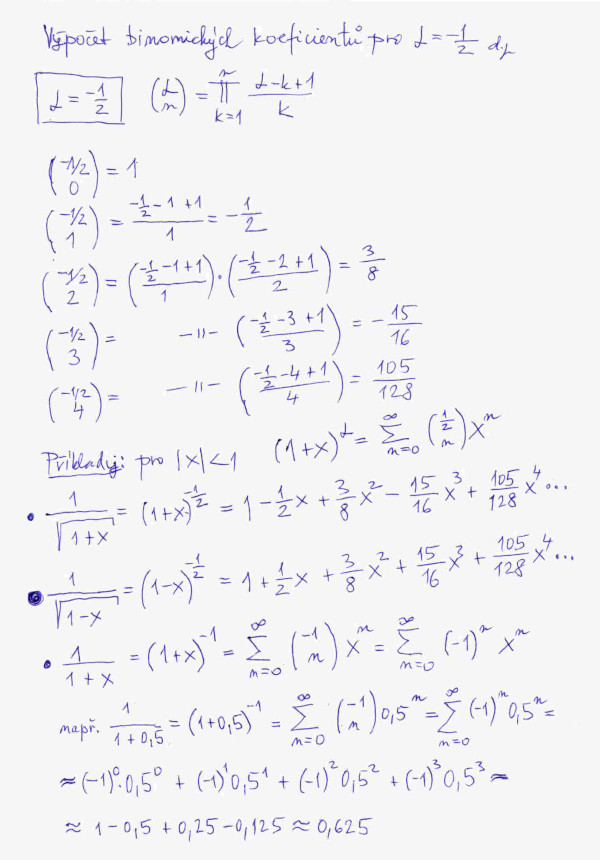
Na obrázku č. 4 je jen pro úplnost uveden výpočet několika prvních kombinačních koeficientů pro alfa = 1/2. I zde uveden jeden příklad na použití nekonečné kombinační řady. Pokud |x| << 1, tak odmocnina z 1 + x se často aproximuje výrazem 1 + 1/x. Vyšší členy rozvoje právě kvůli |x| << 1 lze zanedbat.
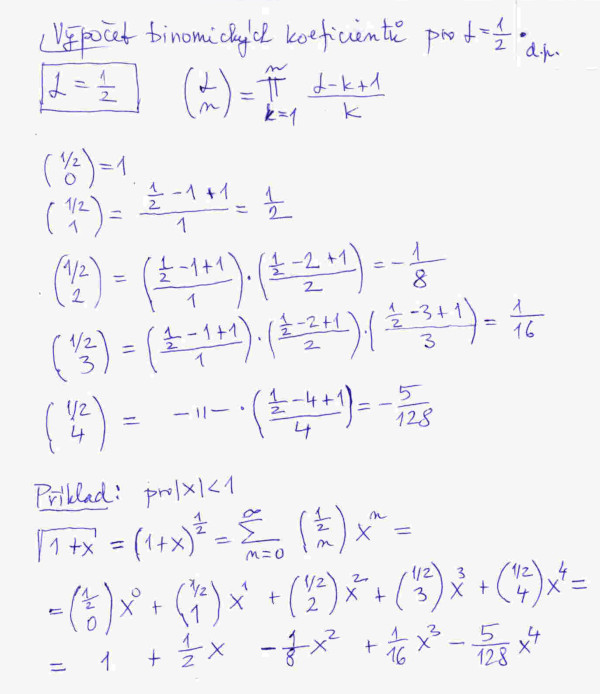
A dostáváme se do finále. Připravili jsme si nezbytný matematický aparát pro vyřešení dvou úloh z úvodního zadání. Na obrázku č. 5 je uvedeno jejich řešení.
V prvním příkladě máme určit vzorec pro kinetickou energii v speciální teorii relativity. V bodě č. 1 je uvedeno řešení této úlohy. Vidíme, že na rozdíl od klasického vzorce pro kinetickou energii, který známe ze středoškolské fyziky, je náš vzorec složitější. Ovšem pokud je rychlost v << c, tak můžeme klasický vzorec považovat za velice dobrou aproximaci hodnoty Ekin. Je to proto, že číselné hodnoty výrazů (v/c)2, (v/c)4 atd. vychází pro v << c velice malé, takže členy binomického rozvoje, které tyto výrazy obsahují, můžeme zanedbat.
V druhém příkladě máme určit přírůstek hmotnosti molekul u plynu, který zahříváme. Ovšem předpokládáme v souladu s fyzikální praxí, že i v zahřátém plynu je rychlost molekul v << c . Tento přírůstek nám vyšel (přírůstek Ekin / c2). Ekin je zde opět klasická kinetická energie molekuly, jak jí známe z fyziky. Vzhledem k tomu že hodnota c2 je obrovská, budeme si muset v domácích potřebách koupit dobré váhy, abychom přírůstek hmotnosti plynu dokázali určit :-).

Snad vás můj text nezklamal, a možná, tedy doufám, že některé dokonce i zaujal. Šanci na to má z jednoho prostého důvodu. Je nepovinný! A to je vše.
V Brně 24. června 2025.