Neutrální bod
Dušan Polanský
Vnučka Jindra, chodí do druhé třídy, mi nedávno s veškerou holčičí vážností sdělila, že nemá ráda slovní úlohy z matematiky. Já jí pro změnu vážně sdělil, že jsem je měl docela rád, ale že jsem neměl rád příklady na formální úpravy, tedy čistě technické výpočty. Ukazuje na její sešit matematiky povídám: „Vyber nějaký těžký slovní příklad a spolu jej vyřešíme.“ Odpověď byla okamžitá a lakonická: „Ne!“ Po chvilce dodala „Dědo, žádný slovní příklad se řešit nebude, teď si uděláme bojovku!“ Pokud pravidla bojovky neznáte, jsou taková, že se lístečky nejprve očíslují, např. od 1 do 10, a pak se na ně napíšou různé úkoly, jeden úkol na jeden lísteček. Lístečky se různě schovají. Hráč (tým) musí všechny lístečky postupně vyhledat a úkoly postupně plnit. Úkol se hodnotí body podle úplnosti jeho splnění. Jinak tuhle hru znají dobře např. skauti. Pochopitelně u skautů se úkoly hledají a plní převážně v přírodě. Takže abych zbytečný úvod nějak uzavřel, slovní úkol jsme neřešili, ale připravili jsme bojovku pro její dva mladší brášky, ale ti z toho jako obyčejně moc nadšeni nebudou.
Asi týden poté jsem při cestě do práce jako obvykle vystoupil na poslední tramvajové zastávce před mým pracovištěm a pokračoval tam dle zvyku pěšky po stejné ulici ve směru jízdy tramvaje. Po chvilce se ke mně přidala svižným krokem kolegyně z práce. Trochu jsem se podivil, protože obvykle přesedne z trolejbusu na tramvaj a nechá se odvézt na další zastávku, z které se musí vrátit kousek proti směru jízdy tramvaje zpět, ale pěší úsek do práce od druhé zastávky je o dost kratší než pěší úsek z první zastávky, takže časově získáte. Stejně bych měl uvažovat i já, ale mě minimalizace času nezajímá, a proto vždy vystoupím na poslední zastávce před mým pracovištěm a šlapu po svých o dost delší úsek, než kdybych ho šlapal z další zastávky. Proč to dělám? Jednak po cestě je trafika, kde obvykle v pondělí podávám sportku, a jednak je docela příjemné jít po širokém chodníku kolem studentských internátů a pak budovy Zemské knihovny, kde málem pokaždé vidím uklízečky sedět na dřevěných schodech před knihovnou a dávat si možná prvního ranního šluka. A proč ne! No, a když vracím po práci opačným směrem, tak se nejednou zastavím ve vinotéce, která je rovněž na stejné trase, takže jaképak časové úvahy.
A tak jak jsme spolu s kolegyní šli a meditovali, kromě jiného i nad tím, kdy se vyplatí vystoupit na první a kdy na druhé, vzdálenější, zastávce. Slovně jsme to hravě vyřešili, ale já si hned vzpomněl na malou Jindru, a že zrovna tohle by mohla být pěkná slovní matematická úloha z praxe na časovou optimalizaci. Pochopitelně ne pro druháka, ale pro šikovného žáka deváté třídy by docela šla. Nakonec lze z toho lehce vyrobit i zjednodušený příklad pro druháka, ale pak již úloha ztratí své kouzlo.
Doraziv ten den domů, hned jsem usedl a příklad vyřešil. Vlastně hned to nebylo, jelikož v plechovém kbelíčku je tak patnáct propisek, ale najít alespoň jednu, která píše, není v poslední době vůbec jednoduché. Můj výpočet vidíte na obrázku č. 1 pod bodem č. 1. Je to docela hezký příklad na řešení rovnice o jedné neznámé.
Zastávky tramvaje jsme označili A a B. Bod N je tzv. neutrální bod, tedy bod, na kterém kdyby stálo pracoviště, tak je zcela jedno, zda pošlapeme z A do práce pěšky, nebo se odvezeme do B tramvají a úsek x proti směru jízdy tramvaje dojdeme pěšky. Při výpočtu vycházíme z podmínky minimalizace času potřebného na cestu do práce. Kromě toho, že nám jde o časovou minimalizaci, je nezbytné za rychlost tramvaje i chodce dosadit rychlost průměrnou, tedy s čekáním na zastávkách, křižovatkách, přechodech pro pěší apod. Kupříkladu v reálu je v úseku AB světelná křižovatka, takže pokud tramvaj má červenou, musí čekat. Také na trase chodce ze zastávky A je přechod pro chodce, a obvykle mám to štěstí, že na něm čekám na zelenou. Další důležitý předpoklad je, že neznáme jízdní řád. Pokud bychom jej znali, což dnes není problém, jelikož většina dospěláků má inteligentní mobil, kde lze v příslušné aplikaci doby odjezdu tramvají vyhledat, tak řešení by asi bylo jiné než v našem příkladu. Velice pravděpodobně výsledkem výpočtu by nebyl jeden či více vzorečků, ale celý algoritmus řešení. Jenomže my chceme, aby úlohu zvládl vyřešit i žák deváté třídy, proto jsme výchozí podmínky tomuto cíli přizpůsobili. Uvádím tyhle skutečnosti proto, že důsledná matematizace určitých problémů je obtížná právě kvůli podmínkám, jež zpřesňují zadání s ohledem na realitu. I proto většina matematiků nemá v oblibě praktické úlohy.

Teď si musíme zodpovědět otázku, kterou bychom si měli položit na konci každého výpočtu: Co jsme vůbec spočetli? Z výsledného vzorce vidíme, že poloha neutrálního bodu je na první funkcí třech veličin: x = f(vch, vt, l). Ale protože l je konstanta, o poloze neutrálního bodu rozhoduje poměr rychlostí, takže důslednější zápis je x = f(vch/vt) při l = konstanta.
Z definice neutrálního bodu víme, že pokud naše pracoviště bude dislokováno přesně v bodě N, je úplně jedno, jakou trasu do práce zvolíme. To je sice pravda, ale přece jenom bychom uvítali vzorec, v němž by figuroval poměr x/l1, abychom názorně viděli dynamiku pohybu bodu N v závislosti na rychlosti chodce a tramvaje. Po krátkém algebraickém mordování (viz dodatek) bychom se měli dopracovat ke vzorci x/l1 = (vt - vch)/(vt + vch). Všimněme si, že pokud by se chodec vlekl jako šnek, tak poměr x/l1 vychází o málo menší než 1, což znamená, že neutrální bod by byl velice blízko středu úseku AB ve směru od bodu B. A pokud je rychlost chodce vysoká, neutrální bod se vzdaluje od středu úseku směrem k bodu B. Pochopitelně poslední dvě úvahy platí při předpokladu stejné rychlosti tramvaje. Podobné úvahy jako jsem udělali pro rychlost chůze chodce bychom mohli udělat pro rychlost tramvaje.
Závěr: Pokud naše pracoviště leží mezi bodem A a N je časově výhodnější zvolit variantu s vystoupením z tramvaje v bodě A a zbývající úsek do práce urazit pěšky. Pokud je pracoviště mezi bodem N a B, je časově výhodnější na zastávce A nevystoupit, pokračovat v jízdě do zastávky B a odtud do práce dojít proti směru jízdy tramavaje pěšky. Z toho je jasné, že pokud nám jde o časově minimální řešení, nikdy bychom neměli chodit přes neutrální bod! Pokud tak učiníme, což já činím, nezvolili jsme časově optimální řešení.
Vždy je důležité výpočet ověřit na konkrétních hodnotách. Takový výpočet vidíte v bodě č. 2. Zde je spočteno, že pokud by pracoviště leželo přesně na pozici neutrálního bodu, tak čas potřebný na příchod do práce je opravdu stejný bez ohledu na zvolenou variantu.
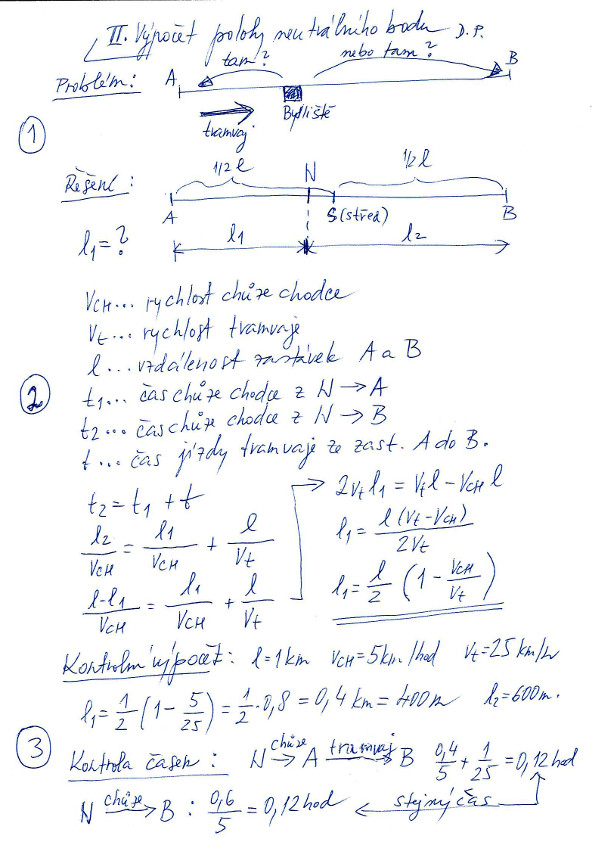
De facto stejná úloha je vyřešena na obrázku č. 2. Bydlíme mezi zastávkami A a B. V bodě č. 1 je graficky formulován problém k řešení: Kam je pro nás časově výhodnější pěšky vyrazit? Na zastávku A, nebo B? Možná, že někdo odpoví, že pokud bydlíme přesně uprostřed (na obrázku je střed označen písmenem S) úseku AB, že je vcelku jedno, ke které zastávce se vydáme. Ale i bez složitého výpočtu je zřejmé, že středový bod S nemůže být neutrálním bodem! Proč? Představme, si že z bodu S vyrazí dva chodci stejnou rychlostí, jeden na zastávku A, druhý na zastávku B. Časy, kdy dorazí do A a B budou sice stejné, ale chodec, jenž vyrazil do A, může mít smůlu v tom, že mu tramvaj ujede přímo před nosem, přitom tu stejnou tramvaj chodec, který vyrazil do B, s velikou pravděpodobností stihne. Vlastní řešení je v bodě č. 2 a v bodě č. 3 je opět časová kontrola výpočtu.
Výsledný vzorec nám vyšel stejný jako na prvním obrázku, což nás asi moc nepřekvapuje, jelikož řešíme da facto stejný problém jako v prvním příkladu. Teď si výsledný vzorec podrobně kvantitativně z cvičných důvodů analyzujeme. Vidíme, že čím bude poměr rychlosti chůze chodce vůči rychlosti tramvaje větší, neutrální bod se bude více blížit k A. A inverzně, pokud bude menší, bude se více blížit k bodu S. A opět platí, že pokud nám jde o minimalizaci času, nikdy bychom neměli chodit přes pomyslný neutrální bod! Výsledný vzorec ošetřuje i případ, kdy vch = vt a kdy nám vychází l1 = 0. V tom případě neutrální bod je v A. Pokud bydlíme jenom kousek od A ve směru k B a rychlost naší chůze je stejná jako rychlost tramvaje, a pokud nám jde o mimimalizaci času, měli bychom vyrazit k zastávce B, ovšem za takovou radu by nám asi většina cestujících pěkně poděkovala.
Již nebudeme podrobně analyzovat vzorec l2/l1 = (vt + vch)/(vt - vch), jehož odvození je uvedeno v dodatku. Jednoduše si dosaďte do vzorce jednou velikou rychlost chodce a podruhé malou a uvidíte zcela názorně jak se bod N bude při menší rychlosti blížit k S ve směru od bodu A. Ovšem pokud jste pozorní, mohli byste mi kontrovat tvrzením, že o kousek výše jsme si čistě logickou úvahou bez výpočtu dokázali, že bod S nemůže být bodem neutrálním, ale přitom když dosadíme do právě uvedeného vzorečku vch = 0, tak nám vyjde neutrální bod v S! Zdůvodnění je prosté, tuhle variantu neuvažujeme, jelikož jednak z pohledu řešeného problému nemá smysl, a jednak kdyby platilo vch = 0, nemohli bychom při našich algebraických úpravách pracovat se zlomky, kde ve jmenovateli je nula, takový výraz není definován. To stejné platí i pro vt = 0.
A pokud jste ještě více pozorní, a vy určitě jste, mohli byste mi zatopit dalším a ne zcela nelogickým dotazem: A co když vch > vt? To se někdy ve špičkách a výlukách klidně může stát. Pokrývá vzorec i tuhle eventualitu? Jistě, pamatuje! V takovém případě nám vyjde, že l1 < 0, tedy že neutrální bod leží před zastávkou A, a z kteréhokoliv místa mezi A a B je výhodné jít na zastávku B, jelikož tím neporušíme základní pravidlo: nechodit přes neutrální bod. Ale logiku to má i bez výpočtu: tramvaj jede pomalejší, než je rychlost naší chůze a my spěcháme a navíc při troše štěstí na zastávce B možná chytneme dřívější tramvaj.
Z obou rozborů k řešeným příkladům vidíme, že analýza a interpretace výsledku, je nedílnou součástí řešení. Velice názorně je to vidět na fyzikálních vzorcích, kde téměř každý vzorec vyjadřuje hlubokou fyzikální zákonitost. Není asi náhoda, že i proto fyzika patří k méně oblíbeným předmětem na školách všech stupňů.
Nakonec s jakýmsi pomyslným neutrálním bodem se setkáváme nejen při cestování. Typické je to při nákupech věcí, které nekupujeme každý den, např. nemovitost, drahá věc sběratelského zájmu, kvalitní sportovní vybavení, automobil. Prodejce má jakousi představu, kupující také, pokud se jejich představy nesejdou v jakémsi pomyslném neutálním bodě, tak se obchod obvykle neuskuteční, jelikož dobrý obchod je ten, v němž jsou nakonec spokojeny obě strany. Nakonec to stejné platí i pro partnerský vztah.
Nevím, zda tady ještě budu, když Jindra bude chodit do devátého ročníku - to bych musel výrazně překonat rodinný rekord, ten je 69 let - a zda moje stránky budou ještě v provozu a tenhle text bude k mání, ale v každém případě žákům a studentům přeji, aby v matematice neviděli strašáka. Strašáci jsou maximálně učitelé, kteří látku vykládají suše a bez jakéhokoliv zaujetí. Ale to neplatí jenom pro matematiku, i život lze žít bez vášně a zaujetí pro něco.
V Brně 12. listopadu 2018.
Doplněk. Zde je uvedeno odvození dvou vzorců použitých v textu.
