Jak na obsah paraboly?
Dušan Polanský
V životě jsem nepotkal člověka, který by potřeboval k něčemu praktickému spočíst obsah paraboly, tím netvrdím, že takový člověk se někdy mezi námi nemotá. Parabola se více používá v literatuře, kde má význam podobenství, viz např. známé Platonovo podobenství o jeskyni. Hodně podobenství najdeme v Bibli v Novém zákoně. Jenomže dnes se nebudeme bavit o literatuře, anobrž o matematice.
Proč právě obsah paraboly? Příčinu to má i nemá. Napadlo mě zadat si do google.cz heslo „obsah paraboly“ a nějak jsem měl pocit, že povídání k tomu nic moc. Tak si povídám, což nějak laicky na úrovni středoškolské látky vysvětlit – ač nejsem učitel ani matematik – jak by se takový obsah paraboly dal spočíst, a navíc čtenáři ještě naservírovat něco navíc oproti středoškolské látce. A nakonec si i sám tím výkladem potrápit hlavu, vždyť za chvíli si již nebudu pamatovat ani malou násobilku. Je mým zvykem předpokládat, že čtenář si již toho moc ze školy nepamatuje, podobně jako já, takže vše se snažím podat od nuly. Ono vůbec něco předpokládat, je dost pochybná investice pro celý život. Kdo něco často předpokládá, obvykle se pak i často diví.
V našem výkladu budeme postupovat docela rafinovaně. Nejdříve si parabolu nakreslíme, pak spočteme její obsah s využitím docela zajímavého vzorečku, který si ale odvodíme až následně. Tohle pomocné odvození nám zabere větší část našeho povídání. Ale tak to již někdy v matematice chodí. Koho by odvození vzorečku nebavilo, jednoduše se na odvození vykašle a půjde si něco dobrého uvařit k snědku nebo si uhasí žízeň nápojem jemu lahodným, případně ušetřený čas využije nebo promrhá jiným způsobem. Ještě jedna technická poznámka. V textu se odvolávám na čísla obrázků, číslo obrázku zjistíte po najetí myší na něj.
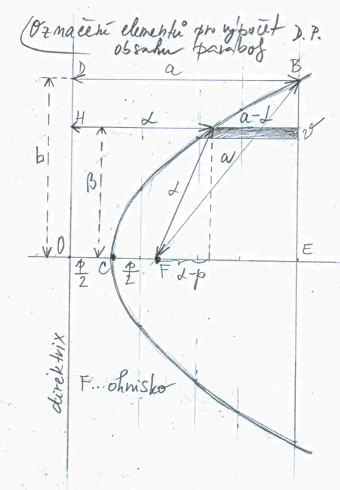
Na obrázku č. 1 máme nakreslenou parabolu a označení elementů, které při výpočtu využijeme. Parabola je docela sympatická křivka, podobně jako kružnice. U kružnice stačí znát polohu středu kružnice a její poloměr a můžeme ji začít kreslit, tedy pokud máme kružítko. S parabolou je to dost podobné. Potřebujeme znát polohu ohniska (F) a jednu přímku, která nesmí procházet ohniskem. Učeně se této přímce říká direktrix. Z bodu F nakreslíme kolmici na direktrix a můžeme začít vynášet body paraboly. Pardon, ještě to nejdůležitější, definice paraboly: body paraboly musí mít stejnou kolmou vzdálenost od přímky direktrix a od ohniska. Ke kreslení je dobré mít po ruce kružítko a křivítko. Nic z toho jsem tentokráte neměl, tak body paraboly jsem vynášel jenom pomocí pravítka, no a body jsem spojoval rukou. Řeknu vám, přesnost nic moc.
Docela důležitý bod paraboly je bod C, říkáme mu vrchol paraboly, leží podle definice přesně v polovině kolmé vzdálenosti mezi ohniskem a přímkou direktrix. Proč právě v polovině? No přece má stejnou vzdálenost od F i od direktrix! Abychom dostali další body paraboly, vyneseme si v různých vzdálenostech několik kolmic na přímku vedenou pod pravým uhlem z ohniska na direktrix, téhle přímce se říká osa paraboly. Kružítkem změříme vzdálenost konkrétní kolmice od bodu O, pak zapíchneme kružítko do ohniska (F), nakreslíme oblouk, a kde nám tento protne uvažovanou kolmici, tam leží dva body paraboly. Postup několikrát zopakujeme s různými kolmicemi na ose paraboly. Pak body paraboly spojíme. A parabola je na světě.
O něco těžší to bude s výpočtem obsahu paraboly, ale nějak si už poradíme. Díváme se stále na obrázek č. 1. Rozdělíme si obsah paraboly (budeme uvažovat jenom obsah nad osou x) na malé vodorovné proužky, jeden takový proužek je na obrázku nakreslený. Pokud budou proužky dostatečně tenounké, můžeme je považovat za obdélníky, spíš takové obdélníčky. Když obsahy obdélníčků naskládaných na sebe sečteme, měli bychom dostat víceméně dost přesnou hodnotu obsahu paraboly. Čím bude výška obdélníčků menší, kupříkladu tisícina milimetru, tím dostaneme obsah paraboly přesnější. Obsah takového obdélníčku umíme lehce spočíst: délka x výška. Výšku si stanovíme sami, ovšem délka se bude měnit v závislosti na umístění obdélníčku ve směru osy y. Nejdelší bude na ose paraboly, nejmenší u bodu B. Neboli přesněji: délka obdélníčku bude určitě záviset od pořadnice beta (jelikož v jazyce HTML beze změny fontu písma, což nechci dělat, nejde psát řecká písmena, proto je píšu celým českým názvem). A ještě od čeho? Jasně, od toho jaký tvar parabola má. Ale tvar paraboly je naštěstí určen jediným parametrem p, což je kolmá vzdálenost ohniska F od direktrix.
Teď již víme, na čem bude záviset obsah paraboly. Bude funkcí vzdáleností a a b a parametru p, matematicky to můžeme zapsat nějak takto: obsah paraboly = f(a, b, p). Teď jde o to, určit přesný tvar funkce. Odvození vidíte na obrázku č. 2. Výška obdélníčku je zde označena osmým písmem řecké abecedy théta. Výpočet se nám ale pěkně zkomplikoval, potřebujeme znát vzoreček pro sumu posloupnosti: 12 + 22 + 32 + ... + n2. V dalším řádku výpočtu je vzoreček uveden. Jak jsem již zmínil, v dalším textu si zmíněný vzoreček pracně odvodíme. Ale čeká nás ještě jedna další nepříjemnost, vzoreček závisí na výšce obdélníčku théta, dvakrát se nám objevuje v čitateli. To se nám jistě nelíbí, proč by měl přesný obsah záviset na výšce obdélníčku? To jako kdyby obsah libovolného pravoúhlého mnohoúhelníku závisel na tom, jak jej kvůli usnadnění výpočtu rozložíme na obdélníky a čtverce, jelikož tyhle obsahy umíme spočíst. Přitom při složitějším mnohoúhelníků těchto rozkladů může být více, ale výsledek musí být stejný. Nakonec i proužky jsme mohli zvolit svislé, ale na velikost obsahu by to jistě nemělo mít dopad. Samotné obdélníčky jsou jenom jakousi pomůckou, pomocí níž bychom dokázali spočíst alespoň přibližný obsah, kdybychom neznali přesný vzorec. Jenomže nám jde o přesný vzorec.

Zkusme se zamyslet nad velikostí dvou zlomků (třetí řádek zdola), v nichž figuruje výška obdélníčku théta. Výšku si můžeme představit ještě menší než tisícinu milimetru, třebas miliontinu milimetru. Uznáte, že pak zlomky, v nichž théta vystupuje, budou tak malé, že asi neuděláme velikou chybu, když tyhle zlomky zanedbáme. A tím je výpočet u konce. Jinak finta se zanedbáním zmíněných dvou zlomků, v nichž vystupuje nekonečně malá veličina (théta) je jádrem diferenciálního počtu. No a představa sumy obdélníčků s nekonečně malou výškou (kdyby byly proužky svislé, tak nekonečně malá by byla šířka obdélníčků) zase jádrem počtu integrálního. Takže pokud jste pochopili výpočet na obrázku č. 2, ale opravdu pochopili, tedy až do morku kosti, pochopili jste celou techniku diferenciálního a integrálního počtu. Vše ostatní kolem jsou již jenom technické záležitosti.
Jádro našeho povídání máme již za sebou. Teď se vrhneme na odvození vzorečku pro sumu: 12 + 22 + 32 + ... + n2. Naše odvození je trochu kostrbaté, ale popravdě zatím lepší a hlavně jednodušší postup neznám. Abych vás za vynaloženou námahu nějak odměnil, pokusil jsem se výklad udělat trochu obecnější, abyste z něho vytěžili i něco navíc.
Na obrázku č. 3 je zopakování základních poznatků o aritmetické posloupnosti. Důležité jsou dva vzorečky: vzoreček pro obecný a současně poslední člen aritmetické posloupnosti a obecný vzoreček pro součet členů aritmetické posloupnosti. Oba zmíněné vzorečky jsou orámovány. Proč jsme si součet označili S1, si objasníme za chvíli. Pro další výklad bude index u písmena S docela důležitý. Že vzorečky opravdu fungují, je ukázáno na dvou příkladech, viz bod 3. K příkladům si vysvětlíme posloupnost kroků výpočtu. V příkladu A je a = 1 a d = 1. Z toho je odvozen obecný tvar člena posloupnosti a obecný vzoreček pro součet členů posloupnosti. Poté je zadán poslední člen posloupnosti, ten je t = 20. Teprve z tohoto údaje odvodíme počet členů naší posloupnosti i hodnotu samotného součtu. Podobně postupujeme v příkladu B.

Teď se podíváme na výpočty na obrázku č. 4. Budou o něco krkolomnější. Chtěli bychom odvodit, čemu se rovná součet posloupnosti: 12 + 22 + 32 + ... + n2, který jsme potřebovali pro výpočet obsahu paraboly. Představme, si obecný člen posloupnosti, který bude tentokráte přesně takový, jaký je obecný vzoreček pro součet posloupnosti S1 na předchozím obrázku. V bodě 1 je ukázán výpočet jednotlivých členů takové posloupnosti. Pro a = 1 a d = 2 budou jednotlivé členy naší posloupnosti právě 12, 22 atd. Pokud tomu nevěříte, podívejte se na obrázek č. 5, tam je uveden konkrétní výpočet. Ale zpět k obrázku č. 4. Vidíme, že součet se nám rozložil na výpočet součtu aritmetické posloupnosti: 1 + 2 + … + n násobené a, a součet jakési posloupnosti násobené pro změnu d. Teď jde pouze to, jak spočíst součet posloupnosti násobené d. K tomu jsme použili umělou rovnost, která nám po malé úpravě nám umožní sečíst členy naší posloupnosti. Tím nám již nebrání, spočíst obecný výraz pro součet S2. Je uveden na obrázku č. 4 úplně dolu v rámečku.

Teď jde jenom o to, jaké dosadit a a d. Na obrázku č. 5 v bodě č. 1 je na konkrétním dosazení ukázáno, že opravdu musí být, jak jsme již dříve uvedli, a = 1 a d = 2. V bodě č. 2 je uveden příklad konkrétního výpočtu. Metodika výpočtu je podobná jako výše. Známe poslední člen posloupnosti, z toho odvodíme, kolik členů musí naše posloupnost mít. Nakonec pomocí námi odvozeného vzorečku spočteme hodnotu součtu. Že výsledek je správný, o tom jsme se přesvědčili prostou sumarizací členů posloupností.

Asi teď již začínáte tušit, že podobně jako jsme spočetli součet S2, bychom dokázali spočíst i součet posloupnosti S3: 13 + 23 + 33 + ... + n3 Jak bychom postupovali? Máte pravdu. Přesně jako při výpočtu S2. Obecný člen naší nové posloupnosti by měl tvar jako obecný součet S2. Indexy u S1, S2, S3 atd. vlastně znamenají, o jakou mocninu členů posloupnosti se jedná. Učeně se takovým aritmetickým posloupnostem říká, aritmetická posloupnost prvního, druhého, třetího atd. druhu. Na střední škole se obvykle učí jenom aritmetická posloupnost prvního druhu.
No a jsme u konce našeho povídání. Pokud vás matematika vyloženě otravuje, zkuste v ní hledat i kousek estetična. Ono vše, co se zredukuje jenom na holou realitu, člověka přestane časem bavit. Nakonec i tak vznešený cit jako je láska, se nejednou transformuje v různé nehezkosti. I mně jedna paní učitelka na základce a jeden pán učitel na střední škole pořádně matematiku otrávili (třebaže ctím, že někteří učitelé jsou od toho přímo placeni), ale jsem si řekl: „Přece ti dva nafoukanci mi nemohou otrávit něco, v čem je i kus krásy.“ A tak jsem začal objevovat krásu matematiky raději sám. Někdy to jde docela lehce, někdy těžce, někdy vůbec, ale důležité je, že je to má svobodná volba, do které mi nikdo nekafre, tedy kromě času, toho se jaksi nedostává.
V Brně 2. listopadu 2016.