Paradox dvojčat
Dušan Polanský
Prolog

Tohle foto – přesněji zde vidíte z něj jenom mnou pořízený výřez – mi poslala vnučka. V dnešních časech omladina umí s foťáky v chytrých mobilech všelijaká kouzla. Popravdě ani mě tak nezajímal trik, kterým se tohoto zvláštního efektu se stínem dosáhlo, spíš to, co opravdu vidím. Měl bych vidět symetrický stín postavy klučiny, jenž ten má ruce u těla, ale u stínu tomu tak není! Začal jsem dumat, k čemu by se tohle foto šiklo, abych něco z fyziky o podobné situaci napsal. Nejprve, že napíšu něco o narušení symetrie ve fyzice elementárních částic, ale zdálo se mi, že je to značné abstraktum a více méně pro laika nezajímavé, a nakonec chtěl jsem vystačit s látkou ze základní školy a trošinkou znalostí z analytické geometrie, a tak mě napadlo sáhnout do teorie relativity a pokusit se vysvětlit paradox dvojčat. Aby se paradox dvojčat projevil, je totiž důležité, aby k porušení symetrie došlo, nějak podobně jako na našem fotu se stínem.
Dilatace času
Abychom si vysvětlili paradox dvojčat, k tomu budeme potřebovat jeden vzoreček ze speciální teorie relativity, jenž stanovuje kvantitativně velikost dilatace času. Pojem dilatace je běžně známý z technické praxe. Kupříkladu na kolejích se dělají dilatační spáry proto, že v létě se koleje vlivem vysokých teplot roztahují neboli dilatují. Pokud jde o dilataci času, od časů Alberta Einsteina víme, že v soustavě, která se pohybuje vůči jiné soustavě větší rychlostí, čas plyne pomaleji, tedy 1 sekunda trvá déle (jako kdyby se natáhla, tedy dilatovala) než 1 sekunda v té soustavě, která se pohybuje menší rychlostí.
Způsobů odvození toho vzorce je známo několik, já zvolil ten, který se mi zdá intuitivně pochopitelný i laikovi. Pokud vám tenhle neexaktní výklad nesedí, stačí si vyhledat z hromady odkazů na internetu nebo např. si můžete prostudovat můj text z roku 2013.
Představte si, že stojíte někde vedle na náspu železniční tratě a pozorujete jak kolem vás frčí rovnoměrnou rychlostí rychlík. V jednom z vagónů někdo vystřelí z pistole střelu napříč tímto vagónem, tedy kolmo na směr jízdy vlaku. Nechť rychlost střely je 400 m/s, což je určitě větší rychlost než rychlost vlaku. Jeden z cestujících ve vlaku má k dispozici velice přesné hodiny, kterými změří čas, který střela potřebuje k překonání šířky vagónu. Při šířce vagónu 4 m je to jedna setina sekundy (4 : 400 = 0,01). Je otázka kolik času zatím uplynulo na hodinách nás, kteří tenhle jev a jízdu vlaku pozorujeme z náspu železniční tratě. Přísně vzato máme zde tři souřadnicové soustavy: železniční trať, jedoucí vlak a soustavu letící kulky, přičemž každá ukazuje svůj vlastní čas, to proto, že absolutní čas neexistuje. Z fyziky je známo, že tyhle časy lze synchronizovat. Koho to více zajímá jak, najde to v každé dobré knize o teorii relativity. Ovšem abychom věci příliš nekomplikovali a šikovně si odvodili vzorec pro dilataci času, a nějak reálně dokázali čas letu kulky změřit, tak jsme si tam zakomponovali jedoucí rychlík. Situace je zřejmá z pohledu shora dovnitř vagónu, viz obrázek č. 2.

Než střela doletí z bodu 1 do bodu 2, vlak se přesune ve směru jízdy do bodu 3. O kolik? O délku v.t’, kde v je rychlost vlaku a t’ je čas, který uplyne na našich velmi přesných hodinkách - tedy těch co máme na ruce v době, když stojíme vedle železniční tratě - než střela překoná šířku vagónu. Jelikož rychlost jízdy vlaku je výrazně menší než rychlost střely, budeme asi předpokládat, že námi naměřený čas t’ bude téměř stejný než čas t, který změřil jeden z cestujících. Jenomže střela z našeho pohledu, tedy pozorovatele z náspu železničního tratě, neletí z bodu 1 do bodu 2 po kolmé přímce ke kolejím, ale přibližně ve směru od bodu 1 do bodu 3. Pokud známe Pythagorovu větu a něco málo z algebry, tak vypočíst vzoreček pro t’ by neměl být větším problémem. A jak to dopadlo, vidíme opět na obrázku č. 2. Výpočet v rámečku dává hodnotu t’ > t. Tedy těm co sedí ve vlaku, nebo nám u náspu železniční tratě uplynul o malý kapánek delší čas než Baronovi Münchhausenovi (po našem Baron Prášil), který běžně létal kdysi na koulích vystřelených z děla, tentokráte by letěl na kulce z pistole.
Jenom dodejme, že u tzv. Lorentzovy transformace, k níž patří i náš vzorec, pod písmenem c si musíme finálně představit rychlost světla: cca 299 792 km/s. Ovšem abychom udrželi jakous takous názornost experimentu, my jsme měřili dobu přeletu šířky vagónu při výstřelu z pistole. Z odvozeného vzorce na obrázku č. 2 je jasné, že jmenovatel v našem vzorci bude vždy menší než 1, jelikož rychlost světla je limitní, přes to totiž nejede vlak. Pochopitelně v různých sci-fi povídačkách často vlak přes to jede.
Paradox dvojčat
Možná vás teď napadne přesně to, co motá hlavu fyzikům od roku 1905, kdy Albert Einstein publikoval svoji práci Zur Elektrodynamik bewegter Körper. Jde o to, že pokud si představíme dvojčata a jedno z nich si vyrazí na výlet pořádně rychlým vesmírným korábem někam pěkně daleko, kupříkladu k nejbližšímu hvězdnému systému Alpha Centuri, tam to otočí a vrátí se na matičku Zem, tak zjistí, že jeho dvojče na Zemi bude kapánek starší než on. Abychom si vysvětlili proč tomu tak je, budeme předpokládat, že koráb letí s rychlostí rovnou 80 % rychlosti světla. Při této rychlosti vychází jmenovatel v našem vzorečku 0,6 (ověřte si to jednoduchým výpočtem!). Aby se nám pohodlně počítalo, uvažujme, že hvězdný systém Alpha Centuri je od nás vzdálen přesně 4 světelné roky (reálně je to asi 4,3 světelného roku); přiznám se, že tuhle hrubou aproximaci jsem zvolil úmyslně kvůli hezkým výsledkům.
Dodejme před naším vysvětlením několik pojmů z fyziky. Světelný rok je vzdálenost, kterou urazí světlo za náš rok, přibližně činí 9,46.1012 km. Rychlost c zvláda jenom foton, který zprostředkovává působení elektromagnetické síly. Pohybovat rychlostí c se může proto, že nemá hmotnost. Žádné hmotné těleso nemůže dosáhnout rychlosti světla c proto, že by k tomu byla potřebná nekonečně veliká energie. Světlo je elektromagnetické vlnění.
Takže jakže to vypadá s tím letem z pohledu nás pozemšťanů? Koráb tedy poletí rychlostí rovnou 80 % rychlosti světla a ať odstartuje přesně o půlnoci ze Silvestra na Nový rok. Teď si představme, že pozemské dvojče po roce pozemského života vyšle, tedy opět po nastoupení Nového roku, novoroční světelný pozdrav svému dvojčeti na korábu. Jak to bude probíhat, si názorně ukážeme na obrázku č. 3.
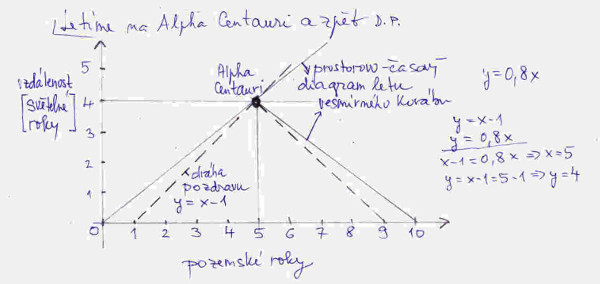
Světočára pohybu našeho světelného pozdravu je vyznačena čerchovanou čárou, její rovnice je y = x – 1. Plnou čárou je vyznačena světočára vesmírného korábu, její rovnice je y = 0,8x. Řešení této soustavy rovnic je: x =5, y = 4; což znamená, že ve stejné chvíli jak dorazí pozdrav ze Země, tak doletí koráb k Alpha Centauri. Pokud by pozemské dvojče vyslalo novoroční pozdrav další Nový rok, ten by již zastihl naše dvojče v korábu na zpáteční cestě. No a pokud dvojče z vesmírného korábu poděkuje za první pozdrav k Novém roku, tak tahle odpověď na zem dorazí právě na Nový rok po devíti letech po startu vesmírného korábu. Vše vidíte na obrázku č. 3. Z obrázku je také zřejmé, že vesmírný koráb se vrátí na Zem po uplynutí 10 pozemských roků. Je otázkou o kolik za tu dobu zestárlo naše dvojče z korábu. Opět nám pomůže náš vzoreček. Víme, že jmenovatel našeho zlomku má hodnotu 0,6; tedy za předpokladu rychlosti korábu 80 % rychlosti světla, takže můžeme napsat, že t = 0,6 . t’ = 0,6 . 10 = 6 let. Takže vesmírné dvojče je po návratu o 4 roky mladší než pozemské dvojče. V reálu by to bylo o něco méně, protože náš koráb hned po startu nemá rychlost 80 % rychlosti světla, a nějakou dobu potrvá než ji získá, při otočení kolem Alpha Centauri musí také kapánek přibrzdit, poté opět se dostat na zmíněnou rychlost, a aby přistál na Zemi, bude muset pořádně šlápnou na brzdu. No a při všech těchto akcích náš vzoreček nefunguje, protože vzorce speciální teorie relativity platí pouze v případě, kdy se obě soustavy vůči sobě pohybují rovnoměrným pohybem.
Pochybovat se má
Leč opatrně, řada fyziků tuto, potažmo velice podobnou, interpretaci paradoxu dvojčat dost vehementně odmítá. Jejich protiargument je zdánlivě prostý: podle teorie relativity přece nezáleží na tom, kdo v reálu letí. Dvojče ve vesmírném korábu si může představit, že vůči němu letí Země a ono je v klidu. Jistě znáte pocit z rozjíždění vlaku, pokud se nedíváme na povrch nástupiště, tak si klidně můžeme představit, že vlak stojí a pohybuje se nástupiště. Ovšem i protiargument k dotyčnému protiargumentu je dost prostý. V případě vesmírného korábu, my co jsme zůstali na Zemi se nechováme symetricky vůči dvojčeti ve vesmírném korábu. Jak jsme se již zmínili, náš koráb hned po startu nemá rychlost 80 % rychlosti světla, a nějakou dobu potrvá než ji získá, při otočení kolem Alpha Centauri musíme koráb přibrzdit, poté opět se dostat na zmíněnou rychlost, a abychom přistáli na Zemi, budeme muset pořádně šlápnou na brzdu. My na Zemi nic takového s matičkou Zemí neděláme, také jak byste např. pohyb Země přibrzdili nebo urychlili? Tedy fyzikálně lze jednoznačně určit, které dvojče je pozemské, a které vesmírné, tedy tady se nejedná o symetrický přístup, jak požaduje princip relativity.
Pokud se vám zdá příklad moc abstraktní tak jiný příklad. Jste jednovaječná dvojčata a bydlíte obě v Brně. Vaše dvojče letí na vědeckou konferenci, která se koná někde na východním pobřeží USA. Když tam přistane, posune si hodiny o 6 hodin zpět. Po návratu z konference si opět musí hodinky nastavit na správný čas, tentokráte o 6 hod vpřed. Vy coby dvojče, které zůstává v průběhu nepřítomnosti vašeho dvojčete stále v Brně, nic takového s hodinkami neděláte, takže každé z vás je fyzikálně jednoznačně identifikovatelné, a tudíž podle teorie relativity po návratu vašeho dvojčete z konference budete o kousek starší než vaše dvojče. Ovšem nemějte obavu, je to o tak nepatrný časový interval, že to nikdo to na vás nepozná. A pokud vás moje sdělení neuklidnilo, vzoreček pro výpočet máte k dispozici, takže si efekt zestárnutí spočítejte. Ovšem nezapomeňte za c dosadit rychlost světla! A to je k fotu vše.
V Brně 31. srpna 2024.