Výpočet posunu hranic pozemku
Dušan Polanský
Byl jsem požádán, zda bych se nepokusil vyřešit konkrétní problém s posuny hranic dvou pozemků. Problém mě až tak matematicky nezaujal, spíš mě zaujala zmínka o pozemcích, přesněji polních parcelách. Je dobré, když má člověk v osobním vlastnictví kousek půdy, kde se může svobodně vrtat jako krtek, tady něco vykopat, onde zahrabat nebo se jenom dívat, jak si plevel spokojeně a zdravě roste. Ani moc nejde o to, co člověk vypěstuje, důležitější je pocit svobodného nakládání s kouskem vlastní půdy. Sice na matičce Zemi mi nepatří ani centimetr čtvercový čehokoliv, ale něco málo patří manželce, přesně 200 m2 z malé zahrádky, a jelikož do obdělávání se nehrne ani majitel druhé půlky zahrádky, tak se o tenhle kousek půdy starám já. Ne sice kvalifikovaně, ale v rámci možností a volného času tak nějak. Když už nohy nemohou, lehnu si na záda, nohy opřu asi tři čtvrtě metru nad zemí o kmen stromu a poslouchám zpěv ptáků. Přiznám se, že i tohle by mě přestalo bavit, jakmile by mi někdo řekl, že něco musím dělat tak nebo onak. To bych skončil, jelikož bych již neměl pocit svobodného nakládání s půdou a hlavně se sebou samým. Stačí, že je člověk řízen v práci.
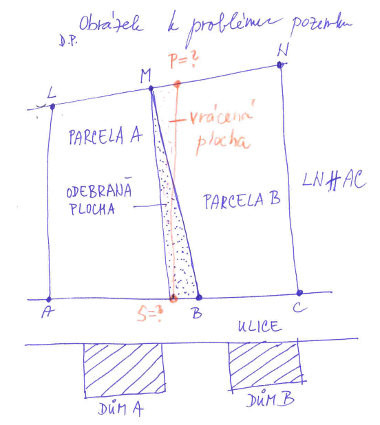
Ale dost filozofických úvah o vlastnictví půdy, raději k našemu problému. Vše je zřejmé z obrázku č. 1; číslo obrázku zjistíte po najetí myši na obrázek. Dva dobří sousedé v jedné hezké vesnici na Jižní Moravě mají vedle sebe nejen domy ale i polní parcely. Parcela A je ohraničena body ABML. Parcela B body BMNC. Bod B leží na přímce AC a bod M na přímce LN. Z dlouhé chvíle sousedy napadlo, že by možná stálo za úvahu, posunout hranice pozemků tak, aby bod S dělil přímku AC, takže za svými domy by měli stejně široké pozemky. Ovšem bod P de musí posunut tak, aby se nezměnila plocha ani jedné z parcel. Důležité je, že přímky LN a AC v našem zadání nejsou rovnoběžné. Kdyby byly, nebylo by vcelku co moc řešit, jelikož oba trojúhelníky by byly stejné pokud jde o tvar. Plocha trojúhelníku, která by se z parcely A v důsledku posunu hranice ubrala, by se parcele A lehce vrátila, stačilo by trojúhelník překlopit. Jak, je zřejmé z obrázku. Ale jinak naše obecné řešení bude platit i pro případ, že AC a LN jsou rovnoběžné přímky.
Aniž bychom se hned zuřivě vrhli na výpočet nebo začali něco datlovat v Excelu či malovat v moderním grafickém editoru, zkusme se raději nad řešením chvíli v klidu zamyslet. Výpočet souřadnic bodu S je triviální; jak se spočtou si za chvíli ukážeme. Horší to bude s bodem P. Představme si, že bod P se pohybuje pomalu z bodu B směrem doprava po přímce LN. Kdy se zastaví, aby byl řešením našeho problému? Máte pravdu, přesně v bodě, kde plocha vrácené plochy SMP bude stejně veliká jako plocha ubrané plochy SBM. Na bod P tedy klademe dvě podmínky: pohybuj se po přímce MN a zastav se ve chvíli rovnosti obsahu trojúhelníků SMP a SBM. Abychom bod P dokázali zakreslit do plánu, potřebujeme jeho dvě souřadnice: xP a yP. Dvě souřadnice jsou dvě neznámé. K jejich nalezení budeme potřebovat dvě rovnice, tak to již v mateamtice chodí. Ale ty rovnice budeme mít k dispozici! První odvodíme z rovnice přímky MN (lze použít i LN) v níž budou figurovat souřadnice bodu P. Druhou odvodíme z rovnice trojúhelníku SMP, budeme totiž vědět jaký obsah plochy má tento trojúhelník mít, přesně jako SBM.
Problém je tímto principiálně vyřešen, teď jenom spáchat šikovně výpočet. Celé řešení zapíšeme obecně, vlastní řešení s přesně zadanými souřadnicemi je již jenom o naklikání např. v Excelu. Co budeme potřebovat k výpočtu? Umět napsat rovnici přímky procházející dvěma body. Najít střed přímky. Spočít plochu trojúhelníku danou souřadnicemi vrcholů a vyřešit dvě rovnice o dvou neznámých. To poslední se za mého mládí učilo v poslední třídě základní devítileté školy. Používali se dvě metody: adiční a substituční. U první metody rovnice násobíme vhodně zvolenými čísly tak, aby se po sečtení rovnic jedna neznámá eliminovala. Opět vše zopakujeme, jenom s cílem eliminovat druhou neznámou. U metody substituční postupujeme tak, že z jedné rovnice vyjádříme jednu neznámou a dosadíme ji do rovnice druhé, čímž se z ní tahle neznámá eliminuje. A opět si postup zopakujeme pro druhou neznámou. Oba postupy jsou dost komplikované, stačí si představit, že máme čtyři rovnice o čtyřech neznámých, to se již člověk zapotí a hlavně výpočet je nepřehledný, a přitom zcela zbytečně. Daleko elegantnější řešení je pomocí determinantů. Vše, co z determinantů budeme potřebovat si vysvětlíme.
Takže nejprve determinanty. Společně budeme sledovat druhý obrázek. Determinat 2. řádu je čtveřice prvků (v našem případě to budou reálná čísla) uspořádaná do čtverce 2 × 2. Aby se poloha prvků v čtverci snadno určovala, používají se indexy. První index znamená řádek, druhý sloupec. Hodnota determinantu je jedno jediné číslo. Jak se tohle číslo spočte je zřejmé z obrázku. Vynásobíme navzájem čísla v diagonále směřující z levého horního rohu do pravého dolního rohu (říká se jí hlavní diagonála) a od takto získaného čísla odečteme číslo získané násobením prvků v opačné diagonále (říká se jí vedlejší diagonála). Obecně u determinatů platí, že jaké znaménko se pro který dílčí součin použije, záleží na směru pohybu. Opět směry pohybu a příslušná znaménka vidíte na obrázku.

Determinat 3. řadu je devět prvků uspořádaných do čtverce 3 × 3. Aby se determinant pohodlně počítal, přidají se vedle původního determinantu dva první sloupec a pak se opět pracuje s diagonálami. O znaménkách platí stejné pravidlo jako u determinantu 2. řádu. Determinant 3. řádu použijeme i pro výpočet plochy trojúhelníka zadaného souřadnicemi. Vzoreček vidíte na obrázku, bez větších problému si jej pamatuji i já, což je malý zázrak, jelikož moje paměť nic moc. Na konci obrázku vidíte, jak se pohodlně s použitím determinantů řeší dvě lineární rovnice o dvou neznámých. E a F jsou pravé strany rovnic, ty musí být známé, nesmí v nich figurovar neznámé x a y. Tolik teorie a teď ji aplikujeme na výše zadaný problém.
Celé obecné řešení je vidět na třetím obrázku. V bodě č. 1 je uvedeno, jak budeme značit souřadnice bodů. V bodě č. 2 je napsán vzoreček z analytické geometrie pro přímku procházející dvěma body, v našem vzorečku tyto body mají souřadnice (x1, y1) a (x2, y2). Co je to za bod (x, y)? To je jakýkoliv bod naší přímky. Teď přijde otázka na test pochopení hloubky tohoto vzorečku. Podívejte se na první obrázek. Jak byste zjistili, že bod B opravdu leží na přímce AC. Odpověď: Do zmíněného vzorečku za (x1, y1) a (x2, y2) dosadím souřadnice bodu A a C a za (x, y) souřadnice bodu B. Pokud se obě strany vzorečku přímky rovnají, bod leží na přímce, pokud ne, tak neleží.

V bodě č. 3 jsou určené souřadnice bodu S ze souřadnic bodu A a C. Je to vzoreček z analytické geometrie, jehož odvození necháme bokem. V bodě č. 4 je spočtena plocha, kterou odebereme z parcely A. Vidíme, že jsme pro vlastní výpočet použili již zmíněný vzoreček pro výpočet obsahu trojúhelníka. Snad uznáte, že zapamatovat si finální tvar je nad možnosti jakéhokoliv pozemšťana, ale pokud si zapamatujeme vzorec v podobě determinatu, tak plochu trojúhelníku spočteme i o půlnoci. V bodě č. 5 je uvedena rovnice přímky procházející body M a N, klidně jsme mohli použít i body L a N, jelikož body L, M a N leží podle předpokladu na stejné přímce. Do této rovnice přímky jsme dosadili za obecný bod na přímce zatím neznámé souřadnice bodu P. Rovnici přímky jsme pak šikovně přepsali tak, abychom na levé straně měli dvě neznáme xP a yP, na pravou stranu jsme hodili to, co spočíst umíme. Pro zjednodušení zápisu si pravou stranu označíme např. E. Vůbec v matematice je důležité si výpočet zpřehlednit, aby se člověk netopil v složitých výpočtech. Už ani nepomyslet na to, že člověk by se hned vrhnul na výpočty s konkrétními čísly, to je vyložené barbarství. Přiznám se, že to jsou i důvody, proč jsem se rozhodl tento příklad zpublikovat. Někdy laici okamžitě dosazují do vzorečků, aniž by předem našli obecné řešení.
V bodě č. 6 jsme vypočetli obsak plochy, kterou budeme muset v důsledku pohybu bodu S doleva vrátit majiteli parcely A. Determinat pro výpočet obsahu plochy trojúhelníku je podobný jako v bodě č. 4, jenom teď v něm figurují souřadnice S, M a P. Na obrázku vidíte výsledek výpočtu s tím, že to, co je známé, jsme opět přesunuli na pravou stranu a pro zjednodušení označili F.
A již jsme ve finále. Máme dvě rovnice pro dvě neznámé xP a yP. V rovnicích jsem provedli další zjednodušení, prvky u neznámých jsme si oindexovali a11 atd. Teď stačí použít jenom vzorečky pro řešení rovnice u dvou neznámých z obrázku č. 2. A je hotovo, výsledkem jsou souřadnice bodu xP a yP. Schválně jsem při zápisu rovnic přehodil oproti obecnému vzorečku na obrázku č. 2 proměnné x a y. Někdy totiž stačí změnit označení a u počtářů to vyvolá zmatek. Když výpočtu rozumím, nemrknu ani okem. Jak si ověříme, že jsme polohu bodu P určili správně? Např. tak, že plochy SBM a SMP se musí rovnat. Pokud se nerovnají, někde jsme udělali chybu. Musíme celý výpočet projít pečlivě znovu. I hledání chyb patří k matematice.
Poznámka ke konkrétnímu výpočtu, např. v Excelu. Nejdřív si pod sebe zapíšeme xové a ypsilonové souřadnice známých bodů: A, B, C, L, M a N. Pak si spočteme souřadnice bodu S. Teď nám nic nebrání spočíst hodnoty koeficientů: a11, a12, a21 a a22. Spočteme si hodnoty pomocných výrazů E a F, jelikož ty budeme potřebovat pro výpočet determinantů v čitatelích výsledních vzorečků. Těsně před finálem spočteme hodnoty determinantů vystupujících ve výsledních vzorečcích pro dvě neznámé. A ve finále spočteme prostým dělením souřadnice bodu P. Nakonec nezapomene na již zmíněnou kontrolu, ověříme, zda se rovnají plochy SBM a SMP. Toť vše.
V Brně 15. února 2015.