O průměrech, odchylce a kvantilech
Dušan Polanský
Asi znáte úsměvné rčení, že statistika je přesný součet nepřesných čísel. Nejednou tomu tak opravdu je. Hodně lidí, včetně mě, má nedůvěru k statistickým průzkumům. Průzkumy se často dělají na objednávku kohosi, a ten nechce výsledek, který mu nebude po chuti. Důvodem nedůvěry k statistickým údajům bude i to, že člověku moc nepomůže, když je na tom podle statistiků dobře, ale přitom v jeho osobním reálu nic moc. Je např. hezké, že naděje na dožití muže narozeného v roce 2013 je 75,2 let (údaj Českého statistického úřadu), když, chudák jedna, v pětačtyřiceti zemře na rakovinu. Statistik řekne, že naději měl, laik že měl především smůlu. Všem je jasné, že kvalita průzkumů je především závislá na spolehlivosti vstupních dat. Pokud taková nejsou, pak opravdu statistika je jenom přesný součet nepřesných císel. Ale proč vůbec utrácím svůj čas na psaní o statistice, když knih kolem statistiky je jako hnoje a kvalifikovaných statistiků ještě více?
V neděli 18. ledna odpoledne po malé procházce na zahrádku (sumárně něco přes 10 km) jsem popíjel u nás v Bystrci v Dřeváku na stojáka výborně chlazené pivo – jak by také chlazené nebylo, když jej piju zásadně venku - a přitom jsem nechtěně a bez většího zájmu poslouchal docela ostré nadávání naštvaného důchodce sedícího u stolu s kamarádem. Nadával na současné poměry, jak také jinak, a rovněž pronesl něco takovéto (silně upraveno, hrubé výrazy vypuštěny): V televizi ve zprávách to je samý průměr, odchylka, kdyby alespoň vysvětlili jaký průměr a jakou odchylku myslí, kdo se má v tom vyznat. No a nedávno mi zase starší dcera vysvětlovala, že v odborných lékařských časopisech se dost často používá krabicový graf. „Co to je za graf, to jsem neslyšel,“ ptám se. „Jak bych ti jej vysvětlila, on totiž ten graf neumí ani Excel, musí se k tomu použít jiná aplikace…“ Asi má pravdu, ale krabicový graf mě zaujal názvem. No a tak coby málem laik v statistice jsem se rozhodl napsat tenhle střípek. Pokud jde o znalosti, vystačíte s matematikou ze základní školy, pouze v jednom důkazu je potřebná znalost základů diferenciálního počtu. Pokud tento počet neznáte, nic se neděje, berte dokázané jako holý fakt.
Začneme trochu obecně. Máme vyšetřit chování nějaké náhodné proměnné, např. výšky dospělých mužů v Brně. Ideální by bylo, kdybychom znali výšku každého dospělého muže v tomto městě. Pak by např. výpočet průměrné výšky byl prostý: např. v Excelu bychom spočetli sumu všech výšek a vydělili ji počtem všech dospělých mužů v Brně. Tím bychom získali jeden z parametrů souboru všech dospělých mužů v Brně, průměrnou výšku. Obvykle se tenhle postup v praxi nepoužívá, jednak proto, že je to drahé, a jednak někdy i organizačně dost těžko realizovatelné. Ze základního souboru (v našem příkladu všech dospělých mužů v Brně) se vybere výběrový soubor, někdy se mu říká vzorek, a statisticky se vyšetří pouze tento výběr. Teorie říká, že pokud je výběrový soubor dostatečně veliký (kolem jeho velikosti je také teorie, ale není nad cit), tak získaná statistika z tohoto souboru, v našem příkladu průměrná výška dospělého muže v Brně, bude velice dobře aproximovat parametr průměrná výška dospělého muže v Brně pro celý základní soubor, tedy všech dospělých mužů v Brně. Ještě trochu další terminologie. Naměřeným hodnotám nějaké náhodné proměnné obvykle říkáme soubor dat. Konkrétní hodnotě z tohoto souboru obvykle znak nebo hodnota náhodné proměnné.
Na obrázku č. 1 – číslo obrázku se vám zobrazí po najetí myší na obrázek – v bodě 1 (další body si zatím nevšímejte) je schematicky znázorněna výchozí situace při statistickém zkoumání základního souboru. Veličinám vypočteným ze základního souboru říkáme parametry, kdežto veličinám vypočteným z výběrového souboru statistiky (neplést se statistikou coby vědní disciplínou). Z obrázku je patrné, jak se provádí výpočet třech základních parametrů základního souboru: aritmetického průměru, rozptylu a směrodatné odchylky a třech základních charakteristik výběrového souboru: výběrového aritmetického průměru, výběrového rozptylu a výběrové směrodatné odchylky.

Než si za chvíli vše ukážeme na příkladu, něco málo si povíme k průměrům. Průměrů je požehnaně, např. aritmetický, vážený, geometrický, harmonický, klouzavý, ten často používají burzovní profesionálové, podobně jako Dow Jones Industrial Average (DJIA). Ten poslední není nic jiného než aritmetický průměr kurzů vybraných akcií. My se zde zmíníme pouze o dvou nejčastěji používaných průměrech: aritmetickém a váženém.
Na aritmetický průměr se často nadává, přitom svoji logiku nadávání někdy má, ale někdy nemá. Občan X nemá žádné úspory v bance, občan Y má milion, takže v aritmetickém průměru má každý půl milionu. Pochopitelně tohle je spíš manipulativní než rozumný statistický výpočet, třebaže na tomhle příkladu je okamžitě vidět základní nevýhodu aritmetického průměru, táhne výsledek směrem nahoru, k vysokým hodnotám. Dokonce v extrémním případě mohou všechny hodnoty, tedy až na tu nejvyšší, ležet nalevo od aritmetického průměru, takže by nám teoreticky mohl vyjít aritmetický průměr platu, na který by nedosáhl kromě největšího pracháče na světě nikdo. Abychom se dopracovali v našem příkladu s úspory X a Y k alespoň jakž takž akceptovatelné hodnotě aritmetického průměru museli bychom vyšetřit větší vzorek osob. Vzorek by navíc musel pokrývat různé skupiny obyvatel. V tomto příkladu by se možná dal zjistit přímo parametr, tj. skutečná výška úspor v bankách na jednoho obyvatele ČR. Šlo by to, kdyby všechny banky by tento údaj zveřejnily s tím, že by se musel technicky ošetřit fakt, že řada lidí má účty v několika bankách. V každém případě aritmetický průměr má pro statistiku (teď myslíme na vědní disciplínu) jednu důležitou vlastnost. Když chceme zjistit reálné číslo, které by mělo tu vlastnost, že součet čtverců odchylek hodnot znaku (např. jednotlivých výšek mužů v Brně) od tohoto čísla je minimální, tak se snadno dokáže, že takovým číslem je právě aritmetický průměr. Proč je tahle vlastnost důležitá? Pochopíte, pokud se podívate ještě jednou pozorně na obrázku č. 1 na vzorec pro výpočet rozptylu. Pokud vás důkaz zajímá, tak jej najděte výše na obrázku č. 1 pod číslem 3, k důkazu je použitý již zmíněný diferenciální počet.
S aritmetickým průměrem těsně souvisí i zákon známý jako regrese ke střední hodnotě. Schválně jsme nenapsali k aritmetickému průměru, protože ne každý náhodný jev lze až tak jednoduše ohodnotit kvantitativně. Zmíněná regrese platí také pro aritmetický průměr, jelikož ten střední hodnotou je. S regresí ke střední hodnotě se setkáváme běžně v životě. To víno i chuťovky v té vinotéce mívali dobré, ale teď se pokazili. Moje politická strana měla minulé dvé volební období výborné výsledky, ale teď je to slabota. Můj fotbalový klub to byla pět sezon bída a utrpení, ale tento ročník vypadá docela dobře, klukům to kope. Minulý rok bylo meruněk jako hnoje, tento rok s bídou na jídlo, zavařovat nebude co. Dva poslední roky v zimě nenapadl sníh a podívejte, letos jej napadlo jako na horách. Tak bychom mohli pokračovat do aleluja. Holt, když se něco daří, počítejme s tím, že příště se pravděpodobně dařit nebude, respektive opačně. Když se daří a nedaří za delší období zprůměruje, máme zde zlatou střední hodnotu. Neboli ještě jinak: "Co jde vzhůru, musí také dolů".
Dopady toho zákona jsou ale i závažnější. Asi víte co je eugenika, je to názor a jakési představy jak zlepšovat dědičný základ a vůbec vývoj populace. Nacisté eugeniku využívali k ospravedlnění své rasové politiky. Hluboce se mýlili nejen oni, ale i mnozí z nás se mýlí ještě dnes. Náhoda má vládu i nad dědičnými tendencemi. V prvním pokolení se vysoce inteligentním rodičům ještě s relativně slušnou pravděpodobností narodí jakž takž chytré děti, ale v dalších pokoleních se již vliv chytrých prarodičů postupně eliminuje právě náhodou. Poznal jsem osobně rodinu, kde rodiče nic moc, ale téměř všechny děti, měli jich šest, vysoce inteligentní lidé. Takže úspěšný, chytrý a hezký partner nemusí být pro inteligenci vašich dětí automatickým požehnáním. Neboli ještě jinak, co je výhra pro vás, nemusí být výhrou pro potomstvo. A je dobře, že tomu tak jest. Naše životy bez vlivů náhody by byly nudnou jednotvárností.

Vážený aritmetický průměr se používá tam, kde musíme zohlednit skutečnost, že určitý znak má nějakou váhu, tj. vyskytuje se vícekrát. Na obrázku č. 2. – jedná se o fragment excelovského listu – je vidět jak se spočte např. průměrná cena benzínu za nějaké období. Cena benzínu se obvykle nemění každý den, ale platí několik dnů. Cítíme, že když vypočteme z cen benzínu aritmetický průměr, náš výpočet nebude asi zcela korektní, jelikož musíme zohlednit i počet dnů, kdy byla cena benzínu stejná. Počty dnů jsou právě ony váhy. K výpočtu váženého průměru byla použita funkce SOUČIN.SKALÁRNÍ. Je to velice jednoduchá a užitečná funkce, nedělá nic jiného, než vynásobí odpovídající si hodnoty ve dvou oblastech, zde ve dvou sloupcích. V našem příkladu výpočet funguje tak, že se každá cena benzínu vynásobí počtem dnů, kdy daná cena platila. Tyto dílčí součiny se sečtou a vydělí se počtem dnů. Vidíme, že aritmetický a vážený průměr jsou rozdílné. Jinak v Excelu je pro výpočet aritmetického průměru přímo funkce PRŮMĚR.
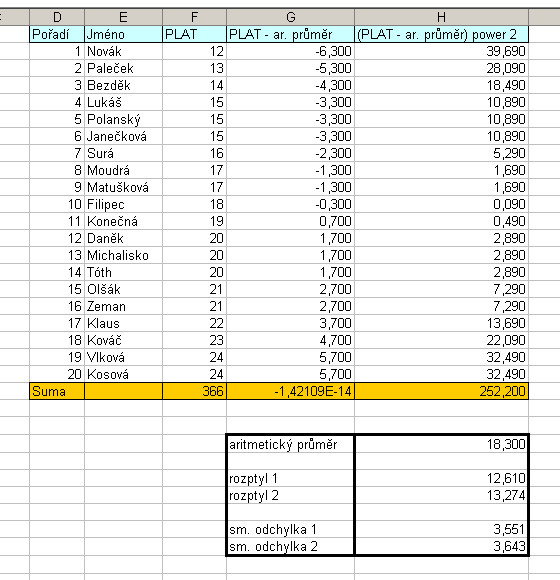
Podíváme se konečně spolu na slíbený jednoduchý příklad. Jeho zadání je prosté. Sešlo se jako zázrakem všech dvacet spolužáků z vysoké školy z jednoho studijního oboru a zavzpomínali na své zaměstnanecké začátky. Každý uvedl svůj nástupný plat po nástupu do prvního zaměstnání. Datový soubor (sadu) vidíme na obrázku č. 3. Je uspořádan vzestupně, to se nám bude hodit při výpočtu kvantilů (viz dále), jelikož ty budeme potřebovat pro nakreslení zmíněného krabicového grafu. Pro zjednodušení jsou výše platů uvedeny v 1000 Kč. Spočíst aritmetický průměr je jednoduché. Vydělíme součet v buňce F22 počtem spolužáků, tj. číslem 20. Ve sloupci G je uveden rozdíl každého platu od aritmetického průměru. Součet těchto rozdílů je velice malé číslo, rovné téměř nule. To, že nevyšla nula, je dáno zaokrouhlením. Triviální důkaz toho, že opravdu součet těchto rozdílů má být nula, je uveden na obrázku č. 1, bod 2. Ve sloupci H je uveden výpočet (PLAT – ar. průměr)2. Součet dílčích mocnin je uvedena v buňce H22. Tuto hodnou potřebujeme pro výpočet rozptylu. Směrodatná odchylka (odmocnina z rozptylu), teď myslíme tu označenou „sm. odchylka 1“ pro celý základní soubor nám vyšla 3,551. Ještě je tam odchylka označená „sm. odchylka 2“. Ta vyšla 3,643. Proč ten rozdíl? Podívejte se na obrázek číslo 1, bod 1. V případě výpočtu směrodatné odchylky z celého základního souboru (a my v tomto příkladu s takovým souborem pracujeme) jmenovatel je n, v případě výpočtu výběrové směrodatné odchylky je jmenovatel je n –1. Vysvětlení, proč tomu tak je, je složitější, proto ji jej odložím na některé z příštích povídání, ale v každém případě v praxi se tenhle vzoreček osvědčil. Odchylka označená „sm. odchylka 2“ je vypočtena pro případ, že by skupina našich 20 studentů byla vzorkem, např. všech studentů, který v stejném roce na škole studium ukončili. Teď se přesuneme za následující obrázek.
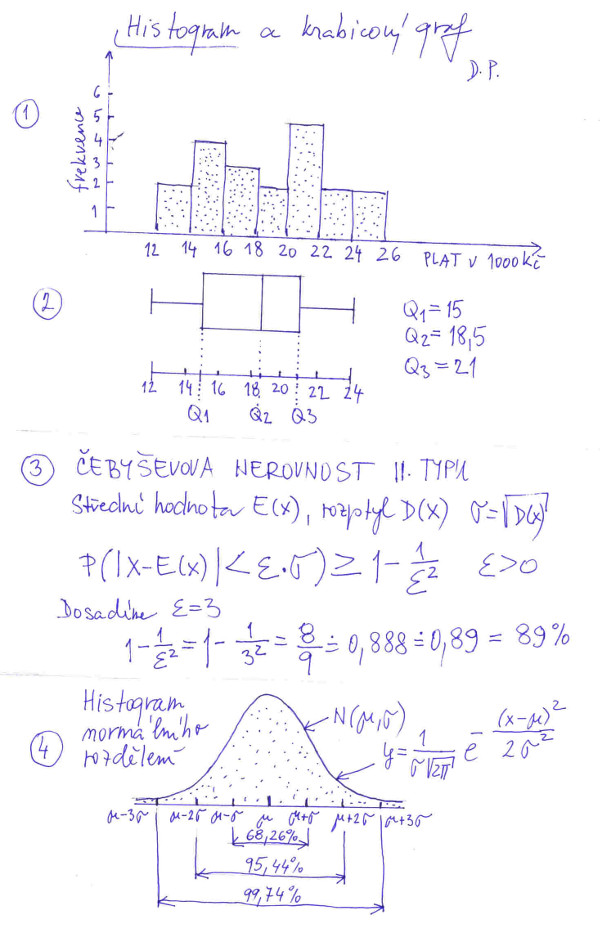
Pokud jde o význam směrodatné odchylky, je to asi takto. Kdyby náš základní datový soubor měl tzv. normální rozdělení, což je takové rozdělení, které má tvar gaussovské křivky, křivka vypadá jako zvon, viz obrázek č. 4, bod č. 4, tak teorie nám říká, že určité procento získaných hodnot (viz obrázek) musí ležet v celých násobcích odchylky na obě strany od aritmetického průměru. Jestliže datová sada nemá normální rozdělení, tak si obvykle vypomůžeme jednoduchým pravidlem plynoucím z Čebyševovy nerovnosti II. typu, viz obrázek č. 4, bod č. 3. Tahle nerovnost říká, že 89 % hodnot náhodné proměnné bude ležet v intervalu ± 3 × sm. odchylka od aritmetického průměru. Histogram zachycující frekvenci výskytu náhodné proměnné z našeho příkladu je uveden na obrázku č. 4, bod č. 1. Na první pohled je vidět, že nemá tvar zvonu, tedy gaussovské křivky. Přesto s 89 % pravděpodobností můžeme tvrdit, že většina hodnot leží v intervalu daném trojnásobkem směrodatné odchylky od průměru na obě strany. Což v našem příkladu bohatě platí, jelikož aritmetický průměr je 18,3 a trojnásobek směrodatné odchylky je 3 × 3,551 = 10,653.
Stále ještě máme jeden dluh a to je onen krabicový graf. Abychom jej uměli nakreslit, k tomu potřebujeme vědět, co jsou to kvantily. Kvantily jsou hodnoty, které dělí datový soubor seřazených hodnot na několik částí se stejnou pravděpodobností výskytu náhodné proměnné. Pokud soubor dat rozdělíme např. na 10 takových částí, tak pravděpodobnost, že náhodná proměnná padne do jedné z deseti částí je 1/10, tj. 10 %. Některé kvantily mají speciální označení. Medián dělí soubor na dvě stejné části. Kvartil na 4 částí, decil na 10 částí a percentil na 100 částí se stejnou pravděpodobností výskytu náhodné proměnné. No a právě kvartily budeme potřebovat pro nakreslení krabicového grafu.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 12 | 13 | 14 | 15 | 15 | 15 | 16 | 17 | 17 | 18 | 19 | 20 | 20 | 20 | 21 | 21 | 22 | 23 | 24 | 24 |
Výpočet mediánu a kvartilů si ukážeme na našem příkladu z obrázku č. 3. Pro pohodlí čtenáře jsem vypsal datový soubor opětovně do jednoduché tabulky. V prvním řádku jsou pořadová čísla uspořádaných hodnot náhodné proměnné, v druhém její hodnoty. Začnemem mediánem. Náš datový soubor má dvacet hodnot, polovina je 10, jenomže když vezmeme 10. pozici, tak vlevo nám zůstane 9 hodnot a vpravo 10. Aby to byl přesný střed, musí to být polovina hodnoty mezi 10. a 11. členem datového souboru, tedy medián je: (18 + 19)/2 = 18,5. Jinak platí obecný vzoreček pro nalezení správné pozice v datovém souboru, je jim (n + 1)/2 člen uspořádaného datového souboru, kde n je počet hodnot celého datového souboru. V našem příkladu (20 + 1)/2 = 10,5. Tedy bereme aritmetický průměr z 10. a 11. člena našeho souboru. Kdyby hodnot bylo 23, tak (23 + 1)/2 = 12. Vlevo od hodnoty mediánu by bylo 11 hodnot, vpravo také. S kvartily je to podobné. Jenom musíme rozdělit uspořádaný datový soubor na 4 části se stejnou pravděpodobností výskytu náhodné proměnné, tedy pravděpodobností 1/4. Rozdělíme 10 hodnot vlevo od mediánu podle našeho vzorečku (10 + 1)/2 = 5,5. A stejně číslo zvětšené o 10 platí pro pravou část od mediánu, tedy 15,5. Na 5. a 6. pozici jsou hodnoty 15 a 15. Průměr těchto hodnot je 15. Na 15. a 16. pozici jsou čísla 21 a 21, jejich průměr je 21. Tím jsme si náš soubor dat, rozdělili na čtyři kvartily se stejnou pravděpodobností výskytu náhodné proměnné. Hodnoty náhodné proměnné v hraničních bodech kvartilů se často značí Q1, Q2 a Q3. V našem příkladu: MIN = 12, Q1 = 15, Q2 = 18,5 Q3 = 21 a MAX =24. No a krabicový graf není nic jiného než dvě krabice namalované nad hodnotami Q1, Q2 a Q3, přesně jak vidíte na obrázku č. 4 v bodě 2. V anglicky psané literatuře se často pracuje s hodnotou Interquartile Range, zkratka IQR, výpočte se ze vzorce IQR = Q3 – Q1, u nás vychází IQR roven 21–15 = 6. Jinak řada statistiků doporučuje právě u průměrného platu neuvádět hodnotu aritmetického průměru, ale hodnotu mediánu. Má daleko názornější vypovídající hodnotu. Když nám statistici sdělí, že medián mzdy je 15 500 Kč, tak to jasně říká, že přesně polovina lidí pobírajících mzdu má mzdu menší než 15 500 Kč, a přesně polovina mzdu vyšší než 15 500 Kč. A to je pro tento střípek již vše.
V Brně ve dnech 19. až 25. ledna 2015.