Maturita a třetí odmocnina z jedné
Dušan Polanský
neboli populárně o obecném řešení algebraických rovnic
Na jaře tohoto roku, právě bylo po písemných zkouškách z tolik proklínané státní maturity, jsem seděl v Občerstvení u lávky na břehu řeky Svratky u piva. Obvykle se tam zastavím při cestě ze zahrádky, dám si jedno a pokračuji dál. Vedle mého stolu se rozjařená skupinka maturantů bavila o obtížnosti písemné zkoušky z matematiky. Na přetřes přišla i třetí odmocnina z jedné, takový příklad totiž v písemce byl. Jedna studentka a jeden student o příkladě tvrdili, že byl jednoduchý, ostatní měli názor přesně opačný. Nechme mladé maturanty diskutovat o tom, zda to byl nebo nebyl těžký příklad a zkusme se na dotyčný příklad podívat z kapánek šiřšího pohledu, ale zase ne moc širokého, abychom se navzájem neotrávili délkou článku. Koneckonců střípek je napsán nematematikem, tj. jedná se především o oddechovou četbu.
Pokud jde o vstupní vědomosti, vystačíme se znalostí výpočtu kořenů kvadratické rovnice na základě obecného vzorečku pro výpočet kořenů této rovnice; dále faktem, že v matematice druhé odmocnině z –1 se říká imaginární jednotka a značí se i (v elektrotechnice někdy j); s intuitivním pochopením některých výpočtů s odmocninami a nakonec se základy rozkladu mnohočlenů. Takže z hlediska požadavků na znalosti jsme v prvním ročníku střední školy.
V našem povídání si neodvodíme ani obecný vzoreček pro výpočet n-té odmocniny z jedné, takový vzoreček totiž existuje a vystupují v něm funkce sinus a kosinus. Pokud vás bude vzorec a jeho odvození zajímat, stačí se podívat do jakékoliv knihy základů algebry. My na výpočty půjdeme co nejjednodušší cestou, tedy podle názoru autora, ostatně sinusy a kosinusy nechme – podle textu známé písničky – hlavám študovaným, my si vystačíme jenom s tím, co jsme si uvedli.
Na prvním obrázku jsem vám naškrábal možný výpočet druhé až čtvrté odmocniny z jedné. Z hlediska algebraického se jedná o řešení třech rovnic: x2 - 1 = 0, x3 - 1 = 0 a x4 - 1 = 0. Pokud jde o řešení rovnice x2 - 1 = 0, k výpočtu kořenů této rovnice jsme mohli použít obecný vzoreček, do něhož bychom za koeficienty dosadili: a=1, b=0 a c= –1. Zkuste si to! Vzoreček je na obrázku uveden. Výsledek by měl být stejný. Abychom zdolali onen maturitní příklad, tj. abychom výpočetli třetí odmocninu z jedné, použili jsem malou fintu. Kubickou rovnici jsme zredukovali na řešení lineární a kvadratické rovnice. Kořeny kvadratické rovnice jsme tentokráte spočetli pomocí již zmíněného obecného vzorečku. Rovněž pro výpočet kubické rovnice existuje obecný vzoreček, který bychom mohli použít, ale čert jej ber, je dost složitý. Obecný vzoreček existuje i pro řešení rovnice čtvrtého stupně (kvartické rovnice), ale jak můžete vidět, při výpočtu čtvrté odmocniny z jedné jsme opět vystačili z postupným rozkladem mnohočlenu na kvadratické a lineární mnohočleny. Napsání výsledku byla již malina.

Teď se zkusme podívat na výpočet páté odmocniny z jedné. Mohli bychom použít onen zmíněný obecný vzoreček se sinusem a kosinusem pro výpočet n-té odmocniny z jedné. Ale domluvili jsem se, že funkcím sinus a kosinus dáme pro tentokráte pokoj. Teď si možná položíte otázku: Když existuje obecný vzoreček pro výpočet kvadratické, kubické a kvartické rovnice, není podobný obecný vzoreček i pro výpočet algebraické rovnice 5. stupně? Kdyby tomu tak bylo, jednoduše bychom koeficienty a, b, c, d, e, f rovnice: ax5 + bx4 + cx3 + dx2 + ex + f = 0 dosadili do takového vzorečku a bylo by vymalováno. Musím vás ale zklamat, přesněji zklame nás všechny mladý norský matematik Niels Henrik Abel (1802-1829). Ten v roce 1824 publikoval pojednání o algebraických rovnicích, kde je dokázána nemožnost řešení rovnice pátého stupně pomocí takového kouzelného vzorečku, který by se dal použít na všechny rovnice 5. stupně. Dokázal, že pro rovnice 5. a vyššího stupně takové obecné vzorečky nejsou a nikdy k dispozici nebudou. Ovšem jeho důkaz netvrdí, že nemohou existovat speciální postupy, jak každou rovnici pátého stupně vyřešit. Na dalším obrázku je jeden takový šikovný postup demonstrován právě při výpočtu páté odmocniny z jedné. Nejdříve jsme si rovnici x5 - 1 = 0 rozložili na součin lineárního a kvartického mnohočlenu, teď by nám již stačilo dosadit do obecného vzorečku pro výpočet kvartické rovnice, ale dle naší dohody chceme vystačit s kvadratickou rovnicí, a proto si zavoláme na pomoc dalšího vynikajícího matematika, Francouze Josepha Louise Lagrangeho (1736-1813), který nám poradí fintu, jak převést řešení rovnice kvartické na kubickou pomocí jednoduché transformace y = x + 1/x. Nejde to vždy, ale v případě naší rovnice, říká se jí reciproká, to jde. Pak je vše jenom počtářská rutina; tu ale popravdě nemám. Hodnou chvíli jsem se musel trápit a rozčilovat, než jsem řešení dostal do výsledného tvaru, který se mi líbí. Určitě není jediný. Dokonce jsem u toho snědl čokoládu Ledové kaštany coby zdroj energie pro výdrž při výpočtu.
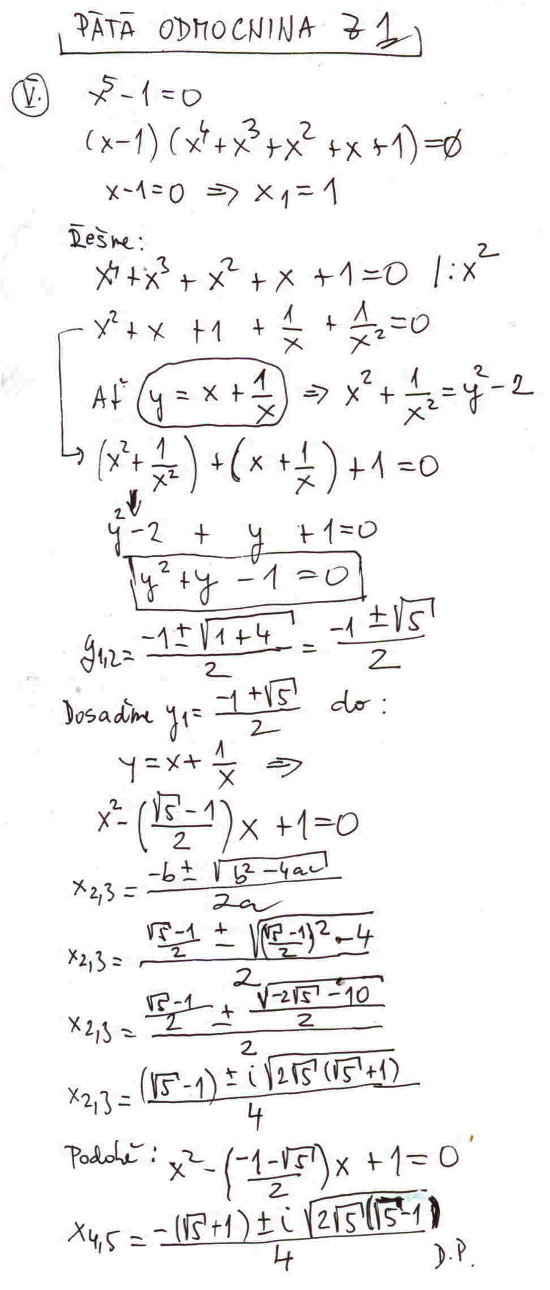
Takže N. H. Abel nás sice pořádně postrašil, ale my jsme si nakonec poradili, i když nemáme k dispozici obecný vzoreček pro výpočet rovnice 5. stupně a nepoužili jsem ani výše zmíněný obecný vzoreček pro výpočet n-té odmocniny z jedné, v němž vystupují sinusy a kosinusy. Teď když nám stoupla stoupla sebedůvěra, mohli bychom vyslovit domněnku: Když budeme šikovní a dostatečně se budeme snažit, je možné, že vždy najdeme takové řešení rovnice 5. stupně, jež bude zapsáno pomocí operací sčítání, odčítání, násobení a odmocňování (dokonce kdyby to šlo, dalo by se vystačit jenom s prvočíselnými odmocnitely) na koeficientech původní rovnice. Když se pozorně podíváme na vzoreček pro výpočet kořenů kvadratické rovnice, v něm vystupují také jenom koeficienty původní rovnice ve čtyřech zmíněných operacích. I výsledné vzorce páté odmocniny z jedné jsou vytvořeny pomocí zmíněných čtyřech operací a koeficientů původní rovnice. Jenomže, bohužel, naše domněnka není pravdivá. Na scénu totiž přichází další mladý matematik, tentokráte francouzský.
Evariste Galois je jedinečnou postavou v dějinách matematiky. Narodil se 26. října 1811 v Paříži. Zemřel v souboji, v květnu 1832, ve věku 21 let. V předtuše smrti, v předvečer osudného souboje, odevzdal svoje nejdůležitější výsledky v dopise svému příteli A. Chevalierovi. Galois předběhl vývoj algebry minimálně o půlstoletí. Aby vyvrátil naši domněnku postupoval přibližně takto. Mějme algebraickou rovnici f(x) = 0 n-tého stupně. Mysleme si napsané všechny možné vztahy mezi kořeny x1, x2, ..., xn rovnice f(x)=0 ve tvaru g(x1, x2, ..., xn), kde g je polynom o n proměnných. Kupříkladu u kvadratické rovnice se lehce zjistí, že platí: že x1 + x2 = –b/c a x1.x2 = c/a. Takových vztahů je jistě nekonečně mnoho. Uvažujme ale pouze ty záměny indexů 1, 2, ..., n, které tyto vztahy převádí opět do správného vztahu. U kvadratické rovnice když zaměníme x1 za x2 a x2 za x1 oba výše uvedené vztahy budou platit stále. Tím dostaneme jakousi množinu operací, která se nazývá Galoisovou grupou dané rovnice. Vlastnosti této množiny jsou směrodatné pro posouzení vlastností dané rovnice, mimo jiného i toho, zda se dá rovnice dá řešit pomocí zmíněných čtyřech operací nad koefiecienty původní rovnice. E. Galois dokázal, že existují rovnice pátého stupně, které nejsou řešitelné pomocí zmíněných operací provedených nad koeficienty dané rovnice. Ovšem to neznamená, že neexistují rovnice 5. stupně, které jsou řešitelné pomocí zmíněných operací provedených nad koeficienty dané rovnice. E. Galois takové konkrétní příklady rovnic uvedl. I my jsme si takovou konkrétní, velice jednoduchou, rovnici 5. stupně vyřešili.
A to je pro dnešek málem vše. Pokud si stále myslíte, že matematika je pěkná otrava, je to asi chyba vašich učitelů, kteří vám neuměli nebo neumí ukázat kouzlo a krásu matematiky, a jenom vás mordují suchými výpočty. Na takové experty jsem narazil i já. Nakonec cestu ke krásám matematiky jsem si našel sám, i když je to cesta pracná. Ale zase má člověk z takového nálezu větší radost. Každopádně jestliže se chystáte k maturitě z matematiky, přeji vám hodně zdaru. Ale mám obavu, že výpočet nějaké té odmocniny z jedné tam již nebude. Ale pro jistotu, zkuste si vypočíst šestou odmocninu z jedné. Je to těžké?! Ale kdepak, zkuste výpočet převést nějakou fintou na rovnici kvadratickou! Jasné, máte pravdu, půjde to pomocí substituce y = x3. Pak stačí využít naše řešení pro třetí odmocninu z jedné. A je to.
V Brně 9. prosince 2012.
Dovětek Přišel dotaz od středoškolské studentky, že si neví rady s rovnicí x4 +1 = 0. Popravdě ani já, tedy dokud jsem na to nedošel, což trvalo dost dlouho. Holt chybí praxe. Háček je v tom, že se musí vtipně vymyslet rozklad a pak nějak šikovně vyjádřit odmocnina z i a -i. Takže raději uvádím celý výpočet.
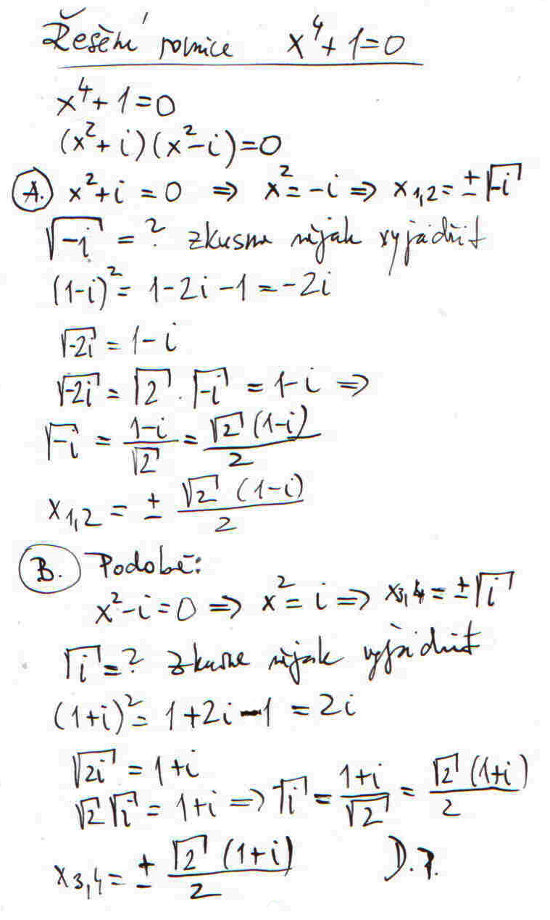
V Brně 17. prosince 2012.