Neděste matematikou!
Dušan Polanský
Něco málo úvodem
Co jsem se kdy bavil s někým o zálibě či nezálibě k matematice v dobách studia na střední nebo vysoké škole, vychází mi z několika málo prezentovaných postojů k matematice čtyři základní typy studentů.
První typ: Matematika mu až tak nevadí, dokonce ho občas i baví, ale nejdou mu cizí jazyky.
Druhý typ: Matematika mu až tak nevadí, dokonce ho občas i baví, a jdou mu i cizí jazyky.
Třetí typ: Matematika je pro něj nutné zlo, které musí vytrpět, ale jdou mu cizí jazyky.
Čtvrtý typ: Nebaví ho ani matematika, ani cizí jazyky, je silně orientován na praxi. Ví, že škola musí vytrpět, a pak hurá do praxe, vydělávat love.
Daly by se uvést i další osobnostní typy, ale uvádím pouze ty, které jsem za roky vypozoroval u lidí, který svůj postoj k matematice v průběhu studia nebo coby vzpomínku na studium nějak vyjádřili. Osobně patřím k prvnímu typu. Dle mého názoru nejméně je studentů druhého typu, obvykle jsou to lidé s vyšším IQ, nejvíce bude asi studentů třetího a čtvrtého typu. Touto klasifikací bych chtěl jenom poukázat na fakt, že matematika coby povinný maturitní předmět je minimálně téma k otevřené diskuzi.
Ono to i se samotnou výukou matematiky je někdy dost problematické, ve škole nás učitelé trápí látkou, s kterou se ani teoretik v praxi moc nepotká, ale zase některé pasáže důležité především pro složitější výpočty si musí člověk dostudovat sám, jelikož na škole se často neprobírají. Obvykle se zdůvodněním, že je to těžká látka a mohla by studentům dělat potíže. Jenomže právě těžkou látku by vám měl pomoci učitel zvládnout! Pokud bojujete s takovou látkou jako samouk, zabere vám to obvykle o hodně více času než s učitelem. Dodejme, že problém je hlubší, neboť i hodiny vyčleněné na matematiku mají také svůj limit.
Nejsem člověk, který by jenom popisně mudroval kolem něčeho, vždy se snažím text osvěžit něčím z toho, o čem se snažím psát. Protože teď píšu o matematice, tak jsem vybral malé osvěžení z propojení goniometrie a pravoúhlého trojúhelníka, tedy něco ze středoškolské látky.
Něco málo z matematiky
Než se dáme do klasického psaní různých vzorců, osvěžíme si dva základní pojmy, a to pojem složené funkce a pojem inverzní funkce. Vyzní to trochu formálně, ale klídek, reál bude sympatičtější. Jinak k hlubšímu pochopení a procvičení si těchto pojmů doporučuji titul [1].
U složené funkce nejde o přímou závislost závisle proměnné (obvykle y) na nezávislé proměnné (obvykle x), tedy ne přímo y = f(x), ale je tam více závislosti, např. pro první platí, že y = f(u) a navíc u = g(x). Tedy y je funkcí x, ale až přes funkci u, neboli zapsáno jinak: y = f(g(x)). Pokud jde o definiční obor složené funkce musíme být opatrní. Nejprve určíme definiční obor funkce y = f(u) a teprve až pak definiční obor funkce g(x). Nikdy ne naopak! Obecně funkce může být i vícenásobně složená, ale s takovou se v tomto textu nepotkáme.
Pojem inverzní funkce je trochu složitější: Nechť je daná funkce y = f(x) s definičním oborem M a oborem funkčních hodnot N. Pokud f(x) má tu vlastnost, že každému y ∈ N je funkčním předpisem x = φ(y) přiřazeno právě jedno takové, že x ∈ M, pro které platí y = f(x), tak funkci x = φ(y) nazveme inverzní k funkci y = f(x). Funkce y = f(x), x ∈ M a funkce x = φ(y), y ∈ N, se nazývají vzájemně inverzní. Zní to docela zamotaně, ale vysvětlíme si to za chvíli názorně na našem příkladu.
Začneme tím, že si připomeneme průběh a vlastnosti funkce inverzní k funkci y = cos(x), která se zove arkus kosinus a zapisuje se x = arccos(y), někdy narazíte i na zápis x = cos-1(y). Tady jsme důsledně použili označení závislé a nezávislé proměnné z naší definice inverzní funkce, ovšem spíš narazíte na zápis y = arccos(x), potažmo y = cos-1(x), pak x = cos(y). Ovšem důležité si je uvědomit, že obor funkčních hodnot funkce y = arccos(x) je úhel v obloukové míře (radiánech) z intervalu [0, π] jehož kosinus je x. Tuhle poslední větu si dobře zapamatujte. Na obrázku níže vidíme, že definiční obor této funkce je [-1, 1] a obor funkčních hodnot je [0, π] v radiánech. Kupříkladu arccos(0) = π/2, protože cos(π/2) = 0.
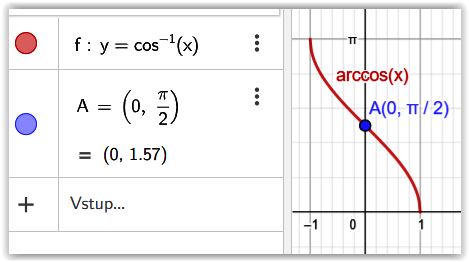
No a teď konečně k našemu příkladu. Víme, že goniometrické funkce, tím i jejich inverzní funkce, jsou definováný pomocí pravoúhlého trojúhelníka. I proto je docela logické, že jakýkoliv funkční vztah mezi goniometrickými, potažmo jejich inverzními funkcemi, musí mít i nějakou geometrickou podobu. Asi moc nepřekvapí, když tahle podoba se zobrazí opět na pravoúhlem trojúhelníku. V našem zadání, viz dále, vystupuje složená funkce f(x)= sin(arccos(x)). Jaký je definiční obor této funkce? Určíme jej ve dvou krocích. Přepíšme složenou funkci do tvaru f(x) = sin(u), kde u = arccos(x). Definiční obor funkce sin(u) je celá reálná osa. Definiční obor funkce arccos(x) je [-1, 1]. Výsledný definiční obor je průnikem těchto dvou oborů, tedy [-1, 1].
Na obrázku níže vidíte důkaz rovnosti mezi složenou funkcí f(x)= sin(arccos(x)) a délkou protilehlé přepony k úhlu theta. Kvůli přehlednosti zápisu píšu např. místo arccos(x) jenom arccos x.

Jinak text tohoto obrázku včetně grafiky byl napsán v LaTeXu a poté vygenerován do pdf formátu, z něhož jsem nasnímal tento obrázek. K úvodu do studiu LaTeXu doporučuji [2]. Při psaní latexového textu mi pomohla i AI, a proč ne, když je tu od toho, aby nám pomáhala. Neposlouchejte moralizátory, co hledají každou muchu na AI! I já jsem u zobrazení trojúhelníku musel trochu doladit detaily, ale to již byla prkotina.
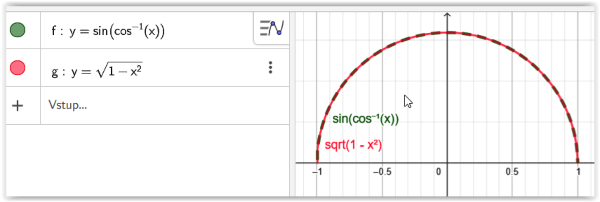
Ovšem je zde stále přirozená otázka, jak je to se znaménkem funkce sin(arccos(x)). Nemůže se stát, že za určité situace bude znaménko záporné? Víme, že funkce arccos(x) vrací úhel z intervalu [0, π], tedy z prvního a druhého kvadrantu. Pro x ∈ [0, 1] vrací arccos(x) hodnoty z intervalu [0, π/2], pro interval x ∈ [0, -1] z intervalu (π/2,π], tedy v obou případech kladné hodnoty. U funkci sin(x) víme, že je v 1. i v 2. kvadrantu kladná. Z toho plyne, že na celém oboru nezávisle proměnné x ∈ [-1, 1] je funkce sin(arccos(x)) ≥ 0.
Nebylo by špatné se teď o celém výpočtu přesvědčit i v grafické podobě. Jak je vidět na obrázku, grafické zobrazení nám potvrdilo správnost výpočtu.
A co závěrem. Vcelku nic, užívejte si léta a nenechte se děsit matematikou děsiči. Kdo má matematiku opravdu rád, ten s ní nikdy neděsí.
Doporučená literatura:
[1] Knichal, Vl., Bašta, A., Pišl, M., Rektorys, K.: Matematika I, SNTL/SVTL, 1965, Praha.
[2] Rybička, J.: LATEX pro začátečníky, 2003, Brno.
Použitý grafický program:
https://www.geogebra.org
Použitý program pro zpracování textu nasázeného v LaTeXu:
https://cs.overleaf.com
Dovětek: Pro ty, co znají základy diferenciálního počtu je na obrázku níže uveden důkaz, že i derivace těhle opticky zdánlivě rozdílných funkcí jsou stejné, což pochopitelně není žádné překvapení, takže spíš to berte jako malé cvičení na derivování dvou složených funkcí.

V Brně uprostřed horkého léta 23. července 2025.