Soustava 2 rovnic o 2 neznámých
Dušan Polanský
Klídek, mým cílem nebude vás naučit řešení soustavy dvou lineárních rovnic o dvou neznámých. Tyhle aktivity rád přenechám učitelům matematiky na základní škole, nemluvě o tom, že tahle látka je na internetu podrobně vyložena snad tisíckrát. Mně jde o něco zcela jiného. Chci vám ukázat, že i zdánlivě běžná látka ze základky postačí k tomu, abychom si vysvětlili látku, která se učí na vysoké škole nejen v matematice, ale i ve fyzice. Mým cílem je vás neotrávit, ale motivovat k zájmu o matematiku a fyziku! Nakonec motivace je možná to nejdůležitější, co od školy očekáváme.
Na prvním obrázku, číslo obrázku zjistíte po najetí kurzoru myši na obrázek, je rekapitulace třech možných výsledků, s nimiž se při řešení soustavy dvou lineárních rovnic o dvou neznámých setkáme. K výsledkům se lze dopracovat různě. Na základce se obvykle podobná soustava řeší buď graficky nebo metodou dosazovací. Protože se jedná o lineární rovnice, obě rovnice jsou současně rovnicemi přímky, když si je nakreslíme, dostaneme výsledek, tam kde se protnou, nebo se chovají jinak, tedy jsou paralelní, pak soustava nemá řešení, nebo dokonce se jedná vlastně o jednu přímku, pak má soustava nekonečně mnoho řešení . Při řešení dosazovací metodou vyjádříme z jedné rovnice jednu neznámou pomocí druhé. Takto vyjádřenou neznámou pak dosadíme do druhé rovnice, čímž dostaneme jednu rovnici o jedné neznámé. Tu vyřešíme a konkrétní hodnotu neznámé pak dosadíme do druhé z rovnic, z které pak vypočteme hodnotu druhé neznáme. Graficky jsem rovnice na obrázku č. 1 neřešil, pouze jsem uvedl, jak to graficky dopadne. U příkladu A to dopadne nejsympatičtěji, přímky se protnou v jednom bodě, jehož souřadnice jsou současně řešením dané soustavy. V příkladu B dostaneme dvě rovnoběžné přímky, které se nikde neprotnou, takže soustava nemá řešení. V příkladu C to dopadne rafinovaně, neboť obě rovnice představují stejnou přímku. V takovém případě má soustava nekonečně mnoho řešení. Stačí si zvolit hodnotu jedné proměnné libovolně a dosadit ji kterékoliv rovnice. Pak stačí už jenom spočíst hodnotu druhé proměnné. Takže potud opáčko látky ze základní školy.

Možná si položíte otázku: Dobrá, pro dvě lineární rovnice se člověk k výsledku dopracuje relativně snadno, ale co když je takových rovnic více, jsou zmíněné postupy nejvhodnější? Popravdě nejsou, neboť jsou pracné. Nejen matematici, ale hlavně ti, co matematiku prakticky používají v praxi, mají v oblibě postupy, které se dají použít mechanicky, bez velkého přemýšlení, tedy finálně se dají i naprogramovat, a pak stačí použít správný program. Tyhle postupy se uplatňují obecně při řešení soustavy n lineárních rovnic o n neznámých, a někdy jsou docela sofistikované, mezi ně patří např. Gaussova eliminační metoda, simplexová metoda. Posledně zmíněná se používá v tzv. lineárním programování. Ovšem zde zmíněné programování nemá nic co dělat s klasickým programováním programovacími jazyky. My si tyhle složité postupy odpustíme. Ukážeme si metodu, která se dá rozumně použít, když se jedná o soustavu několika mála lineárních rovnic, obvykle tak do pěti, ovšem my jsme na základce, takže i nadále zůstaneme u dvou rovnic. Soustavy dvou lineárních rovnic si přepíšeme pomocí matic a k řešení použijeme determinanty. Vše co budeme k tomu potřebovat je na obrázku č. 2. Možná vás to na první pohled vyděsí, ale vězte, že je to jednoduchá látka, třebaže se obvykle učí až na vysoké škole.

Abychom si tuhle techniku procvičili, na obrázku č. 3 jsou vyřešené 4 příklady. Příklady A jsme již vyřešili dosazovací metodou, příklady B a C také nejsou ničím novým, jsou obdobou již námi řešených příkladů. Překvapením asi bude příklad D. Soustava rovnic je již v maticovém stavu a dvě neznáme jsou x’ a t’, přičemž v rovnicích vystupují jako známé hodnoty x a t. Vypadá to zapeklitě, ale je to prosté: známe souřadnice x a t nějaké události v jedné vztažné soustavě souřadnic, a ptáme se jaké budou souřadnice téhle události v soustavě x’, t’ , která se vůči soustavě x, t pohybuje ve směru osy x rychlostí v. Tahle soustava rovnic představuje Lorentzovou transformaci při přechodu od jedné vztažné soustavy k druhé, která se vůči první pohybuje ve směru osy x rychlostí v. Ale zatím příklad berte čistě formálně, tedy jako řešení soustavy dvou rovnic o dvou neznámých.
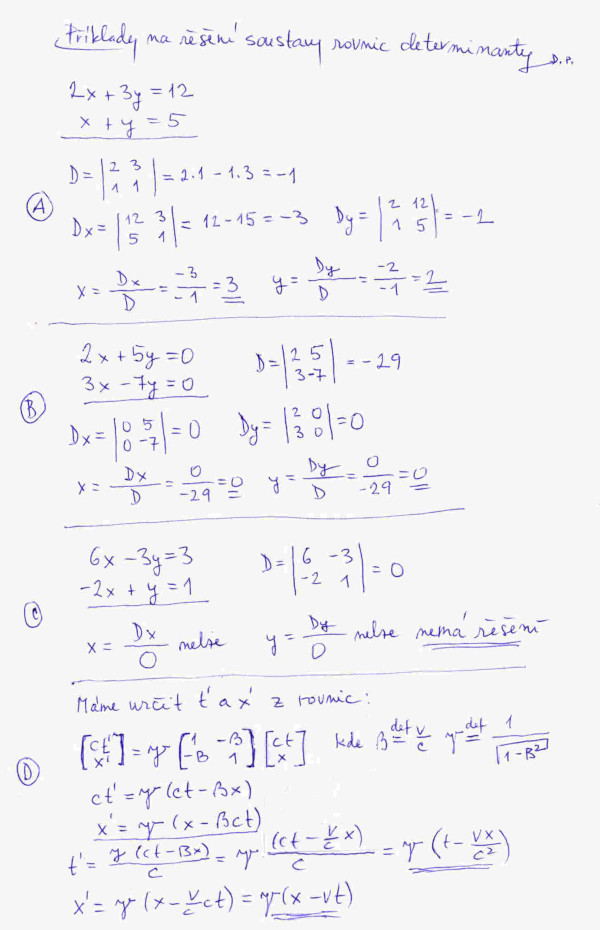
A teď pokročíme. V životě, když si domlouváme s někým schůzku, povíme si, v kolik hodin se sejdeme a kde. Přitom vycházíme z toho, že čas máme na Zemi jednotný, tedy když odhlédneme od časových pásem, ale jinak hodiny všude na Zemi tikají stejně. Kdežto v speciální teorii relativity tomu tak není, každá vztažná soustava má svůj vlastní čas, takže hodiny si v každé soustavě mohou tikat po svém. Domlouvání schůzky v takovém světě by bylo asi složitější, ale uklidním vás, fyzikálně je to realizovatelné přes tzv. kalibraci času. Čas je v našem příkladu zadán zdánlivě rafinovaně, ve tvaru ct, potažmo c t’. Písmeno c zde představuje rychlost světla. Má to jednu výhodu: ct má stejný rozměr jako souřadnice místa x.
Abychom se opět vrátili k Lorentzově transformaci s určitým nadhledem, nejprve ještě jeden příklad, viz obrázek č. 4. Tentokráte budeme uvažovat dvě vztažné soustavy. První, tak jak ji známe z hodin geometrie na základní škole, a druhu pootočenou o určitý úhel proti směru hodinových ručiček. Problém bude opět velmi podobný příkladu D z předchozího obrázku. Tentokráte známe souřadnice bodu P(x’;y’) v pootočené souřadnicové soustavě a ptáme se, jaké budou souřadnice bodu P(x;y) v nepootočené vztažné soustavě. Příklad je opět vyřešen s pomocí maticového počtu a determinantů.

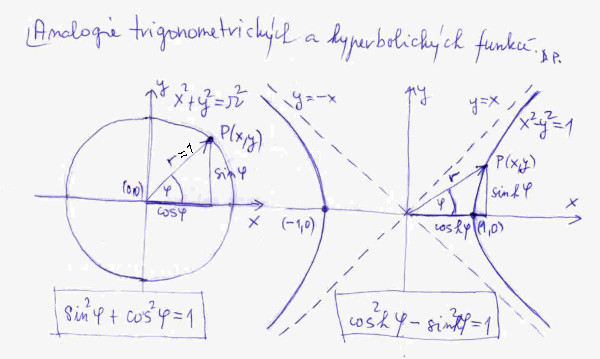
Asi znáte inženýrskou písničku od skupiny Plavci: ... sínus kosínus deskriptíva promovaní inženýři hlavy študované ... A teď trochu něco i o jiných funkcích úhlu než je znáte ze školy, protože my si teď spolu zazpíváme jinou písničku: ... hyperbolický sínus, hyperbolický kosínus, tenhle dědek nás tu pěkně trápí, nás děti školou povinné, jako kdyby sínus, kosínus nebyl už i tak na šlak trefení.
O co jde, je vidět na obrázku č. 5. Jak víte ze školy, trigonometrické funkce jsou odvozené z jednotkové kružnice. Jednotková kružnice proto, že její poloměr je jedna. Platí tam důležitá rovnost, která je uvedena v levé půli obrázku, jinak rovnost automaticky plyne z Pythagorovy věty aplikované na jednotkovou kružnici. Jsou i jiné funkce než trigonometrické, kupříkladu hyperbolické. Jsou pro změnu odvozené z jednotkové hyperboly, která má rovnici x2 – y2 =1. Opět pod obrázkem vpravo je uveden základní vztah, který platí pro tyto funkce. Proč se ve škole učíme trigonometrické a ne hyperbolické funkce? Z praktických důvodů, trigonometrické se používají v běžné praxi více než funkce hyperbolické. Hledět na hyperbolické funkce jako na jakési tajemno či dokonce exotiku, je zcela zbytečné. V dalším výkladu použijeme pouze dvě hyperbolické funkce: sinh a cosh.
A dostáváme se k finále okresního přeboru, viz obrázek č.6. Náš poslední příklad bude na první pohled podobný předchozímu příkladu a dokonce zadání je fyzikálně ekvivalentní Lorentzově transformaci, kterou jsme již poznali z příkladu D na obrázku č. 3. Rozdíl je pouze v tom, že pro zápis Lorentzovy transformace jsme tentokráte použili hyperbolické funkce. Naším cílem bude vypočíst souřadnice bodu P (x;ct) za předpokladu, že známe souřadnice stejného bodu v soustavě, která se pohybuje vůči první soustavě rychlostí v ve směru osy x a její souřadnicové osy jsou x’ a ct’; tedy máme spočíst P(x’;ct’). Výpočet pomocí maticového zápisu a determinantů by vám již neměl dělat větší potíže.
Určitě si teď položíte otázku, proč tak komplikovaný zápis pomocí hyperbolických funkcí, když v příkladu D na obrázku č. 3 je stejná transformace zapsaná na první pohled jednodušeji. Na tento zdánlivě rafinovaný zápis přišel vynikající matematik Hermann Minkowski (1864–1908). Fígl je v tom, že tento zápis umožňuje elegantní geometrickou interpretaci Lorentzovy transformace. A tu si teď vysvětlíme v dolní části posledního obrázku.
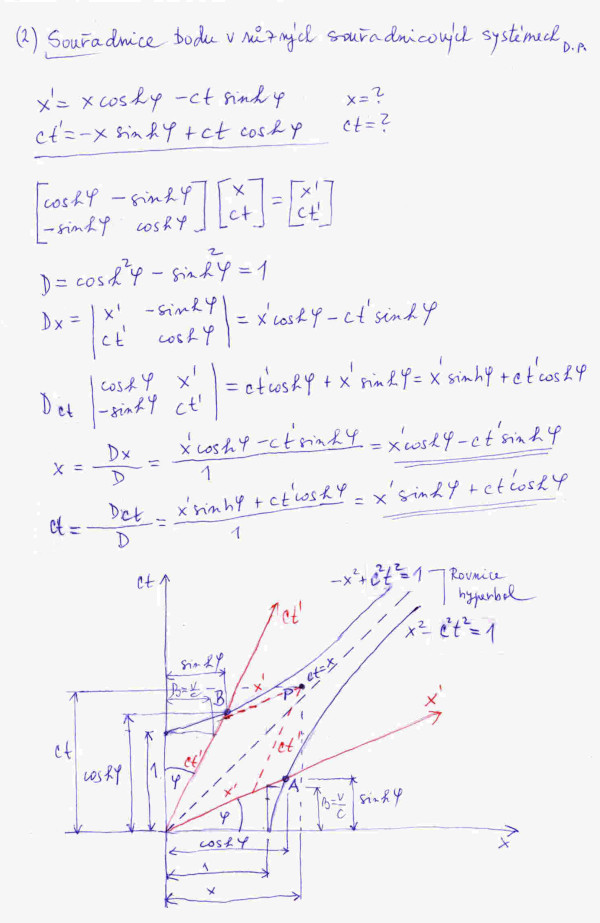
Soustava x, ct je zde nakreslená jako klasická pravoúhlá souřadnicová soustava, kdežto soustava x’, ct’ je kosoúhlá. Sklon jejich souřadnicových os je dán poměrem v/b, kde v je rychlost, kterou se soustava x’, ct’ pohybuje ve směru osy x vůči soustavě x, ct. Na obrázku vidíte dvě větve již zmíněné jednotkové hyperboly. Souřadnice bodů A a B lze snadno spočíst ze zápisu Lorentzovy transformace pomocí hyperbolických funkcí, a uznejte, že jejich souřadnice jsou přímo elegantní. Rovněž z obrázku je jasný význam souřadnic bodu P v obou souřadnicových soustavách. Za zmínku ještě stojí přímka, která má rovnici ct = x, stejně dobře jsme ji mohli zapsat jako ct’ = x’. Je to rovnice světelného paprsku, který se šíří konstantní rychlostí c v obou soustavách, tedy rychlost světla nepodléhá žádné transformaci. Všude je stejná, což je tak trochu na palicu. Představte si, že z louky pozorujte vlak, který frčí kolem vás rychlostí 100 000 km/s a někdo uvnitř vyšle ve směru jízdy světelný paprsek rychlostí 300 000 km/s. Jeden by si řekl, že my z louky naměřímé rychlost světla 400 000 km/s. Kdepak, naměříme jenom 300 000 km/s! Jak jsem již napsal, je to na palicu.
Dodejme, že všechny zde řešené příklady lze řešit i dosazovací metodou, kterou známe ze základní školy. Snad ale uznáte, že pomocí matic a determinantů je to elegantnější a snazší.
Stručně závěrem. Cílem textu není podrobně rozebírat otočení pravoúhlé souřadnicové soustavy o úhel, tedy rotaci, a Lorentzovou transformaci a její důsledky, k tomu viz každou slušnější učebnici geometrie a fyziky, náš cíl byl daleko skromnější. Ukázat, že se znalostí řešení soustavy dvou lineárních rovnic o dvou neznámých se lze při troše námahy dopracovat k zajímavým geometrickým a fyzikálním výsledkům. A možná jsem alespoň jednoho z vás přesvědčil, že matematika umí být někdy i docela zajímavá. Nakonec jako vše, když člověk jde dostatečně do hloubky a je zcela jedno, zda je to duševní nebo rukodělná činnost.
V Brně 25. listopadu 2025.