Něco málo o fyzice tření
Dušan Polanský
Tak trochu zbytečný prolog
Ještě na jaře v Čtyřlístku, nákupní zahradní centrum v Brně v Bystrci, jsem se dal do řeči s pánem lehce po padesátce, tedy tak jsem ho odhadl. Bavili jsem se o hlavně o zahradách. Já osobně sice zahradu nemám, ale starém se o malou zahrádku v společné osadě, kterou napůl vlastní manželka a napůl její bratr. Starám se o ni především kvůli pohybu, ale je pravda, že občas i něco vypěstuji, třebaže půda je samý kámen. To, že kameny musím stále vyhazovat plotem do lesa, kompenzují tím, že v igelitkách nosím do zahrádky koňský hnůj z nedaleké koňské farmy. Taková praktická realizace zákon zachovaní hmoty, třebaže dnes víme, že tento zákon neplatí, že platí zákon zachování energie.
Dotyčný pán se mi, mimo jiné, pochválil tím, že mají u rodinného domu velikou zahradu, napůl okrasnou, napůl užitkovou. Ovšem, že teď má jeden problém, že manželka si kdysi dala dovést do okrasné části veliký kámen, kus přírodní skály, coby zdroj psychické energie. Stačí se o kámen opřít, zavřít oči a na nic kromě kamene nemyslet. Je pravda, že energie přírodního kamene do sebe něco má. Přiznám se, že občas to také praktikuji. Ale zpět k problému dotyčného pána. Jeho paní si na zahradu pozvala psychotronika, a ten jí svatosvatě vážně sdělil, že skála není na dobrém místě, a ukázal na správné místo asi o šest metrů dále. A že manželka teď trvá na posunutí kamene, který má téměř 400 kg. Že problém by to nebyl, kdyby se k balvanu dostala technika, ale protože zahrada již má chodníčky, okrasné záhony atd., tak to jednoduše nejde. Takže jak na to? Je pravda, že se prodávají různé transportní vozíky, stěhováci také mají různé pomůcky, jenže kamen má jednu nevýhodu, nemá pravidelný tvar, kupříkladu jako skříň, tak jak ho chcete dostat na transportní vozíky? Vyslovil jsem názor, že by to možná šlo tažením, kdyby se pod kámen podařilo podložit vhodnou podložku, která má malý koeficient tření vůči kamenu. Přiznám se, že moji úvahu kolem tažení kusu skály s využitím tření jsme do konce nedotáhli, jelikož paní mého společníka ukončila nákup, a manžel musel odnést nákup do auta. Kámen je určitě již na správném místě, ale mě to tehdy nedalo, a za několik dnů jsem si spočetl něco kolem tohoto problému, ovšem papíry jsem založil a ně zapomněl; ne poprvé. No a teď jsem je při hledání něčeho zcela jiného objevil, a tak jsem to dotáhl do ucelenějšího textu.
Fyzika tření
Celá fyzika tření stojí na tomto jediném vzorečku: Ft = f.Fn. Vidíme, že třecí síla Ft zaprvé závisí na síle, kterou je těleso přitlačené k podložce, to je síla Fn. Této síle se říká normálová, protože je k podložce kolmá. V praxi je Fn často tíhová síla, kterou budeme značit FG (G jako gravitace). Pokud bude podložka rovnoběžná se zemí, je Fn shodná se sílou tíhovou. Zadruhé třecí síla závisí na koeficientu smykového tření, tedy velikosti tření styčných ploch. Rozlišujeme dva koeficienty (někdy také součinitele) smykového tření: v klidu (f) a v pohybu (fo). Koeficient fo je vždy větší než f. Lehce si to ověříte jednoduchým pokusem. Položte si např, na podlahu nějaké břemeno a snažte se jej uvést postupným zvyšováním síly (tedy tlačením po podlaze) uvést do rovnoměrného pohybu. Jakmile se vám to povede, pocitově zjistíte, že při pohybu již nemusíte vyvíjet takovou sílu, jako před vyvoláním pohybu. Dodejme, že měřením se zjistilo, že f při malých rychlostech (0,5 až 5 m/s) nezávisí od rychlosti.
Koeficienty smykového tření se uvádí v příslušných tabulkách, bohužel často jsou to hodnoty přibližné, kupříkladu v Matematické, fyzikální a chemické tabulky pro střední školy, mám vydání z roku 2019, je součinitel smykového tření v klidu pro pneumatiku na mokrém asfaltu uveden v rozpětí od 0,2 do 0,5. Pokud byste v praxi potřebovali přesnější hodnotu (není asfalt jako asfalt, a rovněž pneumatika jako pneumatika) je potřebné přesnější hodnotu zjistit měřením. Jak se to dělá, najdete v každé učebnici experimentální fyziky; není to nic složitého.
V dalším budeme společně řešit jednoduché příklady. Než se do toho dáme, připomeňme si Newtonův zákon setrvačnosti, který budeme při výpočtech občas potřebovat: Těleso, na které nepůsobí síly nebo výslednice sil na něj působících je rovna nule, je v klidu nebo rovnoměrném přímočarém pohybu. Explicitně to odvodíme takto. Podle druhého Newtonova pobybového zákona a = Fcel/m = (F + Ft)/m. Pro rovnoměrný pohyb platí: a = 0, z čehož plyne, že F = - Ft. Síla Fn se zase ruší s reakcí podložky, tedy výslednice sil působících na těleso je nulová. Dodejme, že u každého příkladu si po získání řešení uvedeme stručný závěr.
Při jakém sklonu silnice (tzv. elevační úhel) začne zabrzděný automobil samovolně klouzat, když koeficient smykového tření v klidu je 0,3? Řešení je na prvním obrázku (číslo obrázku zjistíte po najetí kurzoru myši na obrázek).
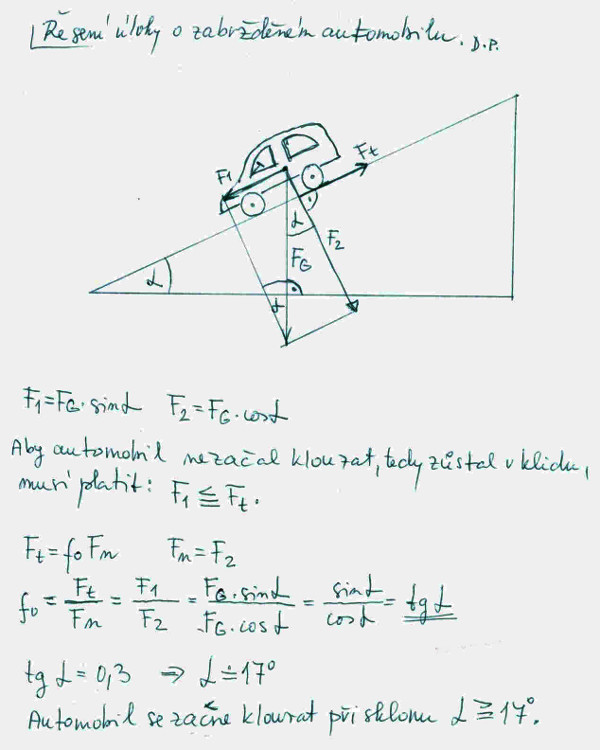
Závěr k příkladu č. 1: Úhel alfa nezávisí na hmotnosti automobilu.
Osobní automobil s počáteční rychlostí 90 km/h je potřeba zastavit rovnoměrným bržděním na vodorovné silnici tak, aby kola neklouzala. Jaký je brzdný čas a brzdná dráha? Součinitel smykového tření v klidu je 0,5. Řešení je na obrázku č. 2.

Závěr k příkladu č. 2: Opět vidíme, že brzdný čas a ani brzdná dráha automobilu nezávisí na hmotnosti automobilu.
Jaká je hmotnost břemena, které táhne motorový tahač rovnoměrným pohybem po vodorovné ploše silou 10 000 N, za předpokladu, že koeficienty smykového tření za pohybu jsou 0,2; 0,5 a 0,8. Řešení je na obrázku č. 3.

Závěr k příkladu č. 3: Hmotnost těles při vyvinutí stejné tažné síly je významně závislá na koeficientech smykového tření za pohybu. Při řešení jsme využili výše zmíněný zákon setrvačnosti, z něhož nám vyšlo, že Ft = F. Proč? Protože břemeno se dle zadání pobybuje rovnoměrnou rychlostí, tudíž výsledná síla působící na těleso musí být nulová. Podle zákona akce a reakce se vyruší síla FG s reakcí podložky a síla Ft se silou F.
Jak velikou práci vykonáme při tažení rovnoměrnou rychlostí kamenného kvádru o hmotnosti 400 kg po vodorovné dřevěné podložce do vzdálenosti 6 m za předpokladu, že tažné lano svírá s podložkou úhel 30 stupňů. Řešení je na obrázku č. 4.

Závěr k č. 4: Vyvinutá tažná síla F je při tomto zadání funkcí třech parametrů: FG, f a úhlu alfa. FG a f jsou konstanty, sílu F lze optimalizovat jedině vhodnou volbou úhlu alfa. Při řešení jsme využili zákon setrvačnosti, z něhož nám vyšlo, že Ft = F. Proč? Protože břemeno se dle zadání pobybuje rovnoměrnou rychlostí, tudíž výsledná síla působící na těleso musí být nulová. Podle zákona akce a reakce se vyruší síla FG s reakcí podložky a síla Ft se silou F.
Jaký je optimální úhel pro tažení kvádru z předchozího příkladu? Řešení s použitím poznatků z diferenciálního počtu je na obrázku č. 5.

Závěr k příkladu č. 5: Optimální úhel pro tažení břemena je úhel, který splňuje podmínku: tg alfa = f. Při dodržení této podmínky tažná síla F je funkcí pouze dvou parametrů: FG a f. Při řešení jsme opět využili výše zmíněný zákon setrvačnosti.
Určete zrychlení soustavy na obrázku č. 6, víme-li že těleso o hmostnosti z klesá a koeficient smykového tření za pohybu je f.
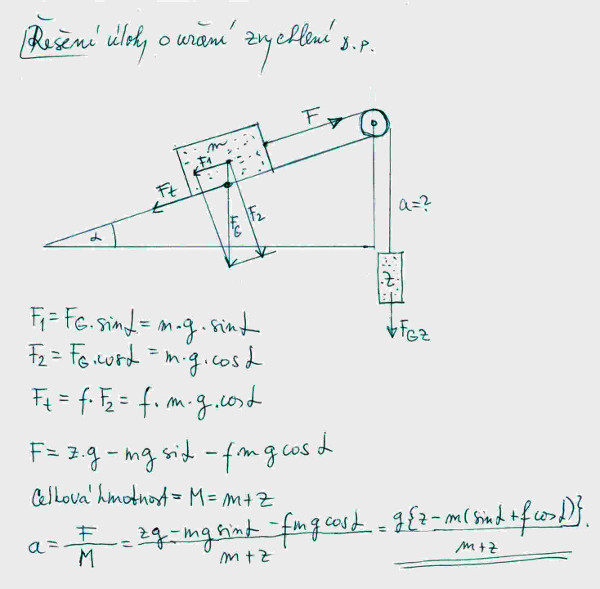
Závěr k příkladu č. 6: Zrychlení a je funkcí hmotnosti těles m a z, dále gravitačního zrychlení g, koeficentu f a elevačního úhlu alfa.
A kratičký závěr závěrem. Bez třecích sil to v našem pozemském životě nejde. Kdyby těchto sil nebylo, nemohli bychom chodit, bruslit, lyžovat, jezdit na kole či jiným motorovým prostředkem. I takový hřebík by byl k ničemu, jednoduše by neplnil spojovací funkci. Bohužel tření nás stojí i zbytečně vynaloženou energii, kupříkladu v pohybových ústrojích motorů, v ložiscích. Abychom tyto ztráty eliminovali, musíme tam, kde je to k prospěchu věci, příslušné povrchy mazat vhodnými prostředy, např. oleji, vazelínou. Ne náhodou se říká, že kdo maže, ten jede. S úsměvem dodejme, že ne jenom v technické praxi. A to je vše.
V Brně 21. září 2022.