Dvojnásobný vektorový součin
Dušan Polanský
Jedna mladá kolegyně z naší organizace mi v jednom rozhovoru o jejím studiu na střední škole řekla, že matematika ji docela bavila, tedy až na ty hnusné vektory. Tak jsem si řekl, že když jsou hnusné, měl bych o nich nějaký ten střípek napsat. A napsal jsem. Pokud jde o vstupní znalosti pro porozumění textu, vystačíme s představou vektoru v intuitivní a názorné podobě, takže mělo by stačit absolvování prvního ročníku střední školy. Dvě malé technické poznámky. Vektory budeme značit tučně, což mě samo o sobě připravilo o tři hodiny života. V jazyce HTML se úhly pomocí řeckých písmen zapsat nedají, tak si je na dvou místech vyjádříme slovním popisem uvedeným v závorce.
Dumaje o čem psát, vzpomněl jsem si na své studium na vysoké škole technického směru. Každý student se v prvním semestru fyziky setká s operacemi vektorový (×) a skalární (.) součin vektorů a pak dokonce se vzorečkem pro dvojnásobný vektorový součin, jeho definici viz dále. Tenhle vzoreček jsme si našich časů pamatovali mechanicky, to proto, že se obvykle zapisuje ve tvaru:
a × (b × c) = b(a . c) – c(a . b).
Pravá strana se pamatuje docela lehce bac – cab, zní to zapamatovatelně: bac mínus cab. Později, to jsem již nestudoval a matematiku jsem téměř nepotřeboval, maximálně na kontrolu výplaty, jsem zjistil, že takhle si vzorec pamatovat byla pěkná pitomina. V dalším si vysvětlíme proč. Pokud se zatím nechytáte, jde vše podle plánu, leč za chvíli bude vše nádherně jinak, jelikož teprve až teď začínáme.
Vektor je veličina, která má tři atributy: velikost, směr a orientaci. Vektory se dělí na volné a vázané. Volnému je vcelku jedno, kde se v prostoru nachází, jenom musí mít stále stejné tři zmíněné atributy. Vázaný je navíc fixován počátkem na konkrétní pevný bod. Pro nás tohle dělení nebude důležité. Vektor umíme definovat i jinak. Uvedeme jeho složky v zvolené soustavě souřadnic ve směru os x, y, z. Složky jsou vlastně průměty vektoru na jednotlivé souřadné osy. V praxi to znamená, že kupříkladu jeden vektor rychlosti můžeme nahradit třemi rychlostmi v směrech souřadných os. Na střední škole se pracuje, pro jednoduchost, s pravoúhlovou soustavou souřadnic, někdy se složkám v takové soustavě říká kartézské složky. S tímhle vyjádřením vektoru budeme v dalším textu pracovat i my.
Pro vektory jsou definovány operace sčítání, odčítání, násobení vektoru skalárem (veličina, která má jenom jeden atribut, např. číslo) a násobení (součin) vektorů mezi sebou. Dokonce jsou definovány dva součiny vektorů mezi sebou, skalární a vektorový. Jak jsme si již uvedli, skalární budeme značit znakem . a vektorový ×. Za chvíli si oba součiny definujeme. Operace dělení není u vektorů definována. Proč? Důvod je v tom, že vektorové rovnice x . a = s, x × a = b nemají jednoznačné řešení pro neznámý vektor x. Kupříkladu u celých čísel je operace dělení definována jednoznačně proto, že umíme jednoznačně vyřešit rovnici: x . 3 = 12. Ze školy víme, že výsledkem je jedno jediné číslo, které je určeno právě operací dělení: x = 12 : 3 = 4.
Teď k vektorovým součinům. Jsou dva, skalární a vektorový. Skalární se spočte relativně jednoduše: a . b = ab(kosinus úhlu sevřeného oběma vektory); a, b jsou velikosti vektorů. Skalární součin je roven nule, jestliže jeden z vektorů se rovná nule, nebo jsou vektory na sebe kolmé, protože kosinus pravého úhlu je roven 0. Vektorový součin je definován trochu rafinovaněji a × b = ab(sinus úhlu sevřeného oběma vektory)n. Písmenem n jsme označili jednotkový vektor současně kolmý na vektory a a b. Vektory a, b, n musí tvořit pravotočivý systém vektorů, názorně to znamená, že když prsty pravé ruky budeme otáčet od vektoru a k vektoru b v kratším směru proti směru hodinových ručiček, tak vzpřímený palec nám ukáže směr jednotkového vektoru n. Vektorový součin je roven nule, když jeden z vektorů se rovná nule, nebo oba vektory jsou rovnoběžné, protože sinus nulového úhlu je nula. Rovněž z definice je zřejmé, že vektorové součiny a × b, b × a se liší pouze znaménkem, viz zmíněné pravidlo pravé ruky. Výsledkem vektorového součinu je tedy vektor a skalárního číslo, tj. skalár. Oba součiny lze definovat i bez úhlů sevřených těmito vektory, mluvíme pak o složkové definici příslušného součinu. Na druhém obrázku na začátku v části „Co víme:“ jsou uvedeny obě složkové definice součinů u vektorů k a l. Vektory i, j, k, jsou jednotkové vektory v kartézské soustavě souřadnic ve směru os x, y, z. Zápis skalárního součinu pomocí složek je jednoduchý, vektorového kapánek složitější, ale platí, že pokud znám složky obou vektorů v příslušné soustavě souřadnic, výpočet je již vcelku jednoduchý. Zatím si část „Co chceme dokázat:“ nevšímejte!

Konečně se dostáváme k důkazu identity a × (b × c) = b(a . c) – c(a . b). Důkaz si ulehčíme malou fintou. Vektory a, b, c si zvolíme šikovně tak, aby se nám jednak dobře počítalo, a jednak abychom si vše dokázali představit v třírozměrném prostoru. Vše vidíte na druhém obrázku. Vektor a jsme si definovali tak, aby hezky směřoval do prostoru, takže má tři nenulové kartézské složky: ax, ay, az, vektor b zase tak, aby ležel na osi x, tím má nenulovou pouze složku ve směru osy x, tj. bx a nakonec vektor c tak, aby ležel v rovině x, y, tj. má složky dvě: cx, cy. Teď nebudeme spěchat, hezky si vektory představíme v prostoru.
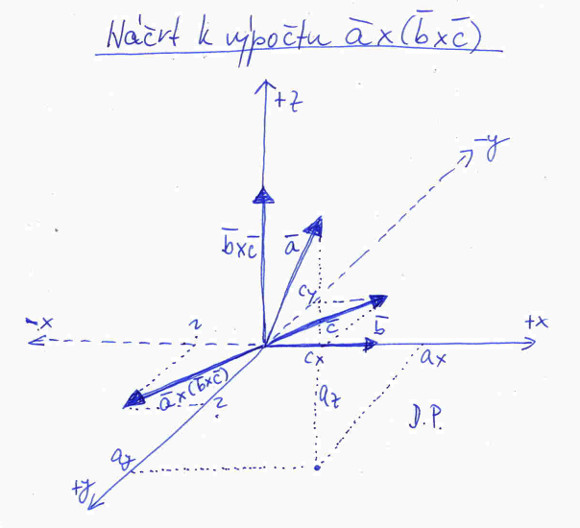
Nejdříve si spočteme levou stranu rovnosti, tj. a × (b × c). Výsledkem bude vektor, protože výsledkem vektorového součinu v závorce je vektor, a vektor vektorově vynásobený vektorem je opět vektor. Kde ale výsledný vektor leží? Podívejme se pozorně na druhý obrázek. Výsledkem vynásobení vektorů v závorce, tj. b × c, bude podle definice vektor kolmý na b i c, tj. bude směřovat ve směru osy +z. Ověříme si to pomocí pravidla pravé ruky, prsty ohýbáme v kratším směru od b k c a palec máme vzorně vzpřímen a vidíme, že má směr osy +z. Teď tento vektor vynásobím vektorem a. Kam bude směřovat výsledný vektor? Opět použijeme pravou ruku, prsty směřujeme od a k b × c v kratším směru, vzpřímený palec nám ukazuje směr roviny x, y. To znamená, že složky výsledného vektoru budou mít obecně nenulové složky ve směru os x a y. Příslušnou část výpočtu vidíte na obrázku č. 1 v části „Co chceme dokázat:“.
Druhá polovina důkazu spočívá ve výpočtu pravé strany rovnosti, tj. b(a . c) – c(a . b). Díky tomu, že jsme si vektory a, b, c zvolili šikovně na míru, výpočet je jednoduchý. Přílušná část výpočtu je opět na obrázku č. 1 v části „Co chceme dokázat:“. Vidíme, že levá strana se rovná straně pravé. Tím je rovnost dokázaná.
Konečně se dostáváme k onomu mnemotechnického pravidla bac mínus cab. Zkusme trochu přemýšlet. Zjistili jsme, že výsledný vektor leží v rovině x, y, tedy v rovině, kde leží i vektory v závorce, tj. vektory b a c. Víme, že libovolný vektor ležící v rovině definované jinými dvěma vektory lze jednoznačně vyjádřit jako lineární kombinací těchto dvou vektorů, tedy v našem příkladu: a × (b × c) = koeficientbb + koeficientcc. Dokázali jsem, že koeficient u vektoru b je roven a . c a u vektoru c je roven – a . b.
Pravidlo k zapamatování výsledku dvojnásobného vektorového součinu by mohlo tedy znít nějak takhle: Dvojnásobný vektorový součin tří vektorů se rovná rozdílu dvou výrazů. První výraz (menšenec) vznikne vynásobením vektoru umístěného uprostřed původního výrazu skalárním součinem dvou zbývajících vektorů (na jejich pořadí nezáleží). Druhý výraz (menšitel) vznikne vynásobením druhého vektoru ze závorky skalárním součinem dvou zbývajících vektorů (na jejich pořadí opět nezáleží).
Zkuste si pravidlo vyzkoušet u dvou příkladů na konci obrázku č. 1. Závorky jsou schválně zadané jinak, než tomu bylo v původní rovnosti. V druhém příkladě sice opět vystupují známé vektory a, b, c, ale protože jsou jinak uzávorkované, pravidlo bac – cab nám není nic platné.
Na závěr si spočteme vektorový součin p × (q × r), přičemž vektory jsou: p = i – j + k, q = 2i – 3j + 2k, r = 4i + j – 3k. Víme, že p × (q × r) = q(p . r) – r(p . q). Nejdříve vypočítáme výrazy v závorkách: p . r = (i – j + k) . (4i + j – 3k) = 4 – 1 – 3 = 0; p . q = (i – j + k) . (2i – 3j + 2k) = 2 + 3 + 2 = 7. Výsledek: q(p . r) – r(p . q) = (2i – 3j + 2k)0 – (4i + j – 3k)7 = 7(– 4i – j + 3).
Teď si v našem původním výrazu posuneme závorku: (p × q) × r. Jiný tvar dle našeho pravidla bude: q(p . r) – p(q . r). Skalární součin p . r máme již spočten, ten je 0. Ještě si vyčíslíme skalární součin q . r = (2i – 3j + 2k) . (4i + j – 3k) = 8 - 3 - 6 = -1. Výsledný vektor nám vychází: -(i – j + k)(-1) = i – j + k. Vidíme, že praktické výpočty jsou na rozdíl od důkazu jednoduché.
V Brně 6. dubna 2014.