Nezneužívejte matematiku!
Dušan Polanský
Něco kritického úvodem
S tím zneužíváním nemyslím teď na matematiky, protože matematik může těžko matematiku zneužít, tedy pokud nemá v povaze se vytahovat na žáky a studenty, ale spíš na ty, kteří často šikovně zneužívají některé matematickými pojmy.
Kupříkladu u politiků takovým často zneužívaným matematickým pojmem je aritmetický průměr (AP). Jak víme, AP je součet všech hodnot vydělený počtem hodnot. Kupříkladu AP hodnot 2, 3, 5 a 10 je 20/4 = 5. Matematici mají AP ve veliké oblibě už jenom kvůli tomu, že když spočtenou hodnotu AP vynásobíte počtem hodnot dostanete stejnou sumu, jako když jste sečetli všechny hodnoty, v našem příkladu 5 × 4 = 20.
Paradoxně pro to stejné se AP hodí i politikům v souvislosti s uváděním např. průměrné mzdy, ovšem ze zcela jiných pohnutek. V době když píši tento text, je v ČR průměrná mzda cca 46 924 Kč. Vypadá to hezky. Jenomže když se podíváte na medián, ten je 38 385 Kč. U mužů dosáhl 41 677 Kč, u žen 35 226 Kč. Pro připomenutí medián je hodnota, která se nachází přesně uprostřed ve skupině vzestupně seřazených hodnot, v našem případě platů. To znamená, že polovina posuzovaných platů je menší než medián a druhá polovina je větší než medián. V našem příkladu to znamená, že polovina lidí v pracovním poměru bere mzdu nižší než je 38 385 Kč. No a to už tak hezky nevypadá, jako když se uvede, že průměrná mzda je 46 924 Kč. No a u žen je to ještě horší, polovina z nich bere mzdu nižší než 35 226 Kč. Pokud se podíváte na statistické údaje z minulosti, lehce zjistíte že rozdíl mezi průměrnou mzdou a mediánem postupně roste. Dnes je cca 8 000 Kč. Takže pokud se dáte na politiku, nikdy u mezd neuvádějte AP, protože medián je férovější.
V další dám již s AP pokoj, budu se věnovat jinému dost často zneužívanému pojmu, a tím je pojem pravděpodobnosti. Znáte to, protože se u nás rozvádí cca 50 % manželství, tak máte pravděpodobnost, že když vstoupíte do posvátného stavu manželského, že se s 50 % pravděpodobností rozvedete. Jenomže pravda to není, jelikož jsou borci a borkyně, kteří to zvládnou za život vícekrát. Také občas statistici vyrukují s tvrzením, že se rozvádí méně manželství než v minulosti. Také to není celá pravda, on je tu totiž i pohled sociologický. Důvod poklesu rozvodovosti je ten, že dnes více párů žije „na divoko“ a spíš do stavu manželského vstupují lidé, co to myslí s manželstvím více vážně než jenom jako dočasnou záležitost. Jednou, když budou všichni žít na divoko, budeme mít rozvodovost nulovou, tedy s úsměvem. Ovšem matematicky to sedět bude. Sociologicky a ekonomicky to bude, opět s úsměvem, hotová katastrofa, protože všechny ženy s dětmi budou svobodné maminky a budou pobírat sociální dávky.
Zadání příkladu
Abych s pravděpodobností také jenom nemanipuloval, společně si vyřešíme jeden zábavný příklad, dokonce čtyřmi postupy. Začneme zadáním.
Sedm studentů vyrazilo na prázdniny do země OX, v níž platí přísné celní předpisy. Dva z našich studentů se pokusí kvůli finančnímu přilepšení přepašovat přes hranice kontraband. Celník na hranici zcela náhodně ukáže prstem na tři z nich a podrobí je důkladné celní prohlídce. Jaká je pravděpodobnost, že odhalí alespoň jednoho pašeráka?
K řešení budeme potřebovat základní pojmy z teorie pravděpodobnosti a kombinatoriky. Připomeneme si jenom to, co budeme potřebovat pro naše výpočty. Tímto opáčkem, se vyhneme tomu, aby nám někdo předhazoval: Jak to, že to neznáte, vždyť to jsme již brali!
Základní pojmy z teorie pravděpodobnosti
Míru možného uskutečnění určitého jevu nazýváme pravděpodobnost. Pravděpodobnost je dána zlomkem, podílem počtu příznivých výsledků k hledanému jevu a počtu všech možných výsledků. Jev jistý je takový jev, který nastane při každém pokusu, jeho pravděpodobnost je 1. Opakem jevu jistého je jev nemožný, ten nikdy nemůže nastat, jeho pravděpodobnost je 0.
Příklad: Při poctivém házení „necinknutou“ hrací kostkou je počet všech možných výsledků roven 6, může padnout 1 nebo 2 nebo 3 nebo 4 nebo 5 nebo 6. Pravděpodobnost pádu šestky je pak 1/6, jelikož pouze jeden výsledek je příznivý pádu 6. Jak to dopadne, když budeme chtít vědět, jaká je pravděpodobnost jevu, že padne 1 nebo 5? Víme, že 1 a 5 nemohou padnout najednou, to by byla velice divná kostka, tyhle jevy se vylučují, i proto takovým jevům, které nemohou nastat současně, říkáme navzájem se vylučující jevy. Když při hodu padne 1, již nemůže padnout 5 a opačně. Věta o sčítání pravděpodobností nám říká, že pravděpodobnost vzájemně se vylučujících jevů je rovna součtu pravděpodobnosti těchto jevů. Pravděpodobnost pádu 1 je 1/6, stejnou pravděpodobnost má pád 5, tedy opět 1/6. Výsledná pravděpodobnost, podle zmíněné věty, pak bude 1/6 + 1/6 = 2/6 = 1/3. Ještě jiný výpočet. Všech možných výsledků je 6, příznivé našemu jevu jsou ale pouze dva výsledky: pád 1 nebo 5. Podle definice pravděpodobnosti je výsledek dán podílem příznivých případů, ty jsou 2, k celkovému počtu možných výsledků, těch je 6. A opět jsme u stejné pravděpodobnosti: 2/6 = 1/3.
Pokud hodíme kostkou dvakrát a ptáme se, jaká je pravděpodobnost, že padne v obou případech 6, tak výsledek spočteme podle věty o násobení pravděpodobnosti. Ta tvrdí, že pravděpodobnost současného nastání více nezávislých jevů (hody kostkou takové jsou) získáme vynásobením pravděpodobností jednotlivých jevů. V našem příkladu 1/6 * 1/6 = 1/36.
Nakonec ještě zmíníme jev opačný k jevu A. To je takový jev, který nastane, pokud nenastane jev A. Pravděpodobnost opačného jevu k jevu A = 1– P(A). Kupříkladu, když pravděpodobnost narození kluka je 0,51, tak pravděpodobnost narození holky je 1 – 0,51 = 0,49.
Něco málo z kombinatoriky
Budeme toho potřebovat málo. Kombinační číslo udává počet kombinací, tj. způsobů, jak vybrat k prvků z n prvkové množiny. Přitom nezáleží na uspořádání k prvků ve vybrané skupině. Spočte se podle vzorce: C(k, n) = n!/k!(n – k)! Faktoriál je definován takto: n! = 1*2* … *n. Příklad: Kolika způsoby můžeme vybrat skupinu 3 studentů ze 7 studentů, kterým předem přidělíme čísla 1 až 7. Výpočet nám dává: C(3, 7) = 7!/3!(7–3)! = 35. V našem příkladě uspořádané 3 prvkové skupiny: (1, 3, 5), (1, 5, 3), (3, 1, 5), (3, 5, 1), (5, 1, 3) a (5, 3, 1) tvoří jenom jednu k-prvkovou kombinační skupinu, např. označenou (1, 3, 5).
Pokud na uspořádání k prvků v skupině záleží, tak mluvíme o variacích. Vzorec pro výpočet k-prvkových variací zní: V(k, n) = n!/(n-k)! Příklad: Kolika způsoby můžeme vybrat skupinu 3 studentů ze 7 studentů, kterým předem přidělíme čísla 1 až 7, za podmínky, že na uspořádaní prvků v skupině záleží, tedy např.: (1, 3, 5), (1, 5, 3), (3, 1, 5), (3, 5, 1), (5, 1, 3) a (5, 3, 1) jsou u výpočtu k-prvkových variací různé skupiny, kdežto u kombinací to byla jedna jediná skupina. V našem příkladu V(3, 7) = 7!/(7-3)! = 210. Je to logické: pokud kombinačních skupin je 35, a z každé 3 prvkové skupiny se dá vygenerovat 6 různých uspořádaných 3-ntic, tak 35 * 7 = 210. Počet 6 jsme zjistili přímým vypsáním, ale opět se dá určit podle vzorce P(n) = n!. Písmeno P je zkratka za permutace. V našem příkladu: P(3) = 3! = 1*2*3 = 6.
Řešení našeho příkladu
Slíbil jsem čtyři řešení. Začneme tím, že si nakreslíme tzv. pravděpodobnostní strom. Vidíte jej na obrázku č. 1 vlevo; číslo obrázku zjistíte po najetí kurzoru myši na příslušný obrázek. Písmeno K znamená = ten, co pašuje kontraband, písmeno N je student, který nic nepašuje. Jak jsme jej vytvořili? Vžijte se do postavení studentů, vžít se do postavení celníka by nebylo správné, neboť ten neví, zda vůbec nějaký pašerák mezi studenty je. Možná cit a zkušenost mu říká, že alespoň jeden pašerák by mezi mladíky mohl být. Studenti ví, že mezi nimi jsou 2 pašeráci, a že celník si namátkou z nich vybere tři. Při výběru prvního má šanci, že kápne na pašeráka 2/7, že nekápne 5/7. Při výběru druhého vybírá ze šesti studentů, pokud kápnul na K již při prvním výběru, pravděpodobnost kápnutí na toho druhého je pouze 1/6, protože jeden K byl odhalen při prvním výběru. Při třetím výběru celník vybírá už pouze z 5 studentů. Pokud kápnul na K při prvním i druhém výběru, již nemůže dalšího K odhalit, neboť jsou pouze dva K, proto ta nula nahoře a tutově ten třetí je N, proto ta jednička. Podobně se nakreslí další větve stromu.
Víme z výše uvedeného povídání o kombinatorice, že celník může vybrat, pokud nezáleží na pořadí studentů, celkem 35 trojic studentů, pokud záleží na pořadí dokonce 210 trojic. Ovšem není nutno pro každou takovou trojici kreslit pravděpodobnostní strom, bylo by to zbytečné, strom na našem obrázku vlevo je univerzální. Pokud tomu nevěříte, zvolte si dva studenty, kteří budou K, a nakreslete si pravděpodobnostní stromy pro několik různých 3-ntic studentů, v kterých budou zastoupeni K, potažmo i strom, kde nebude žádný K.
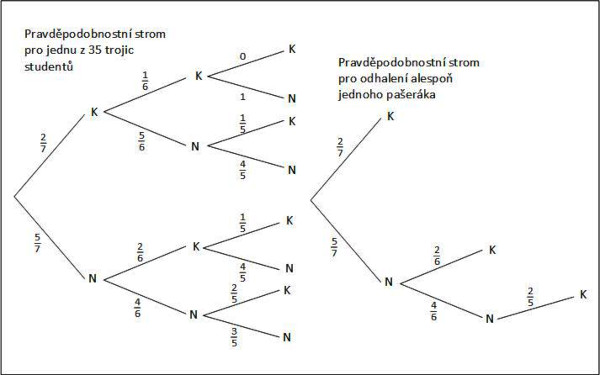
No a teď konečně přistoupíme k prvnímu řešení. Stačí aplikovat větu o sčítání a násobení pravděpodobnosti na náš strom. Půjdeme po všech cestách (cesta obsahuje dílčí větve) které nás dovedou alespoň k jednomu K a budeme postupně násobit pravděpodobnosti zapsané nad větvemi konkrétní cesty našeho stromu. Sčítat budeme přes jednolivé cesty. Horní cesta je nulová, tu vypustíme. Rovněž spodní cesta (N, N, N) nemá pro nás význam. Celník vybral trojici, ve které není ani jeden pašerák.
2/7*1/6*1 + 2/7*5/6*1/5 + 2/7*5/6*4/5 + 5/7*2/6*1/5 + 5/7*2/6*4/5 + 5/7*4/6*2/5 = 5/7. Odpověď: Celník má pravděpodobnost 5/7, že kápne alespoň na jednoho K. Že nekápne ani na jednoho je 1 – 5/7 = 2/7.
Druhé řešení bude elegantně krátké. Podívejte se pozorně na náš strom vlevo, konkrétně na spodní cestu. Pokud celník bude postupovat podle ní, má smůlu, neodhalí ani jednoho K. Jaká je pravděpodobnost téhle cesty? Máte pravdu: P(N) = 5/7*4/6*3/5 = 2/7. Pokud je pravděpodobnost, že celník neodhalí ani jednoho K, pak opačný jev, tedy že odhalí alespoň jednoho K, musí být podle věty o opačné pravděpodobnosti P(K) = 1– 2/7 = 5/7.
Třetí řešení také nebude také moc složité. Podívejte se na obrázku č. 1 na druhý strom, ten vpravo. Co nám říká? Je to minimální strom odhalení alespoň jednoho K. Spočteme podle tohoto stromu pravděpodobnost P(K) = 2/7 + 5/7*2/6 + 5/7*4/6*2/5 = 5/7.
Čtvrté řešení nebude vycházet z pravděpodobnostního stromu. Podobné úlohy se řeší i jinak, než jsem vám vysvětlil, ani ne tak kvůli větší názornosti, ale kvůli efektivnosti a jednoduchosti výpočtu.
K řešení použijeme tzv. hypergeometrické rozdělení pravděpodobnost. Používá se, když z konečného souboru objektů (7 studentů) náhodně vybíráme několik objektů (celník vybírá náhodně 3 studenty), a počítáme pravděpodobnost, že mezi vybranými bude přesně určitý počet objektů s nějakou vlastností např. K (student je pašerák s kontrabandem).
Vzorec hypergeometrického rozdělení vypadá divoce, ale není tomu tak. Ve jmenovateli je počet trojic, které lze vytvořit ze 7 studentů, už víme, že jich je 35. V čitateli je součin dvou činitelů. První činitel říká kolik skupin lze vytvořit ze dvou pašeráků, pokud má být v trojici např. jeden pašerák, v tomto případě jsou to dvě skupiny. Druhý činitel je počet skupin po dvou studentech z 5 hodných studentů. Po dvou proto, že v prvním činiteli vystupují skupiny po jednom pašerákovi a 1 + 2 = 3. Součin činitelů je tam proto, že zmíněné počty skupin jsou za zvoleného počtu pašeráků v trojici na sobě nezávislé. Když se nad tím důkladně zamyslíte, tak je to vlastně vzorec klasické pravděpodobnosti: ve jmenovateli je počet všech možných trojic, a v čitateli počet trojic, které vyhovují určité podmínce.
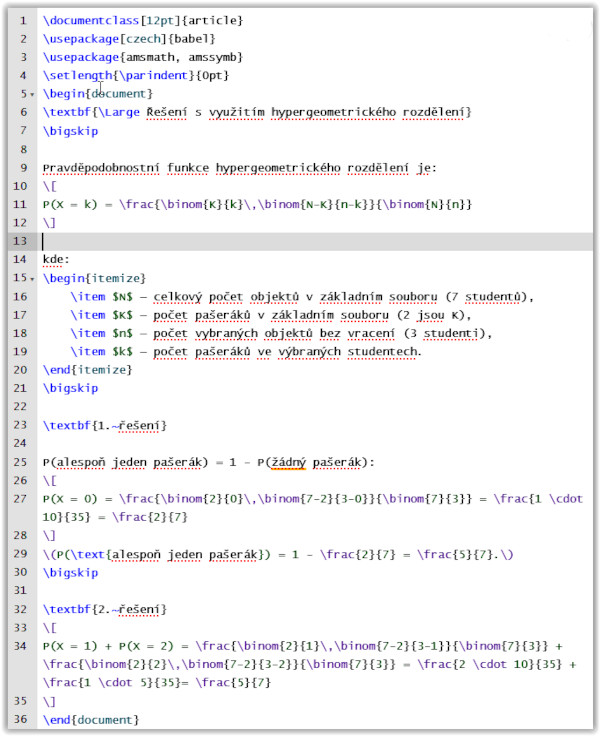
Naši úlohu vyřešíme pomocí hypergeometrického rozdělení dvěma způsoby, viz obrázek č.2.

Ještě poznámka k textu „počet vybraných objektů bez vracení“. V našem příkladu jde o to, že když celník náhodně vybere prvního studenta, a poté co provede jeho kontrolu, nepošle ho, aby se opět zařadil k nevybraným studentům, a pak následně bude vybírat dalšího studenta opět ze 7 studentů. Kdyby už byla tma a celník by neměl svítilnu, mohl by vybrat stejného studenta. Pro náš příklad nemá tento postup z pohledu celníka žádnou logiku, studentům by ale vyhovoval, měli by větší šanci, že nebudou pašeráci odhaleni. Ovšem jsou úlohy, v kterých se vybraný objekt vrací zpět do základního souboru objektů, je to proto, aby pravděpodobnost výběru jednotlivých objektů byla konstantní. Koneckonců na našich pravděpodobnostních stromech je názorně vidět, že jednotlivé pravděpodobnosti se v průběhu výběru studentů k celní kontrole postupně mění, a to právě proto, že vybraný student se již nevrací k nevybraným kolegům, zůstává bokem, i proto statistici mluví o postupném výběru objektů bez vracení. A to je z pohledu teorie pravděpodobnosti vše, ale ...
Všichni víme, že je zde nový fenomén zvaný AI, a pokud jste s touhle dámou již o něčem z matematiky komunikovali, možná jste si všimli, že vše v pozadí generuje v sázecím programu LaTex, že vám to pak zobrazuje do klasické podoby, to je již výsledek generování do formátu pdf. Na ukázku, jak takový text vysázený v sázecím programu LaTex vůbec vypadá, jsem připojil obrázek č. 3. Takhle jsem napsal v Latexu text na obrázku č. 2. Pak jsem jej nechal vygenerovat do formátu pdf programem Overleaf.com (je free na internetu). Nejsem žádný extra znalec LaTexu, takže se předem znalcům LaTexu omlouvám, pokud něco není napsáno echt metodicky. Zkuste text na obrázku č. 2 napsat v textovém editoru Word. Ovšem bacha, půjde vám o nervy :-).
V Brně 18. srpna 2025.