Minkowského prostoročas
Dušan Polanský
Článkem Zur Elektrodynamik bewegter Körper v 17. čísle časopisu Annalen der Physik v roce 1905 Albert Einstein (1879–1953) položil základy speciální teorie relativity. Dne 21. září 1908 Hermann Minkowski (1864–1909) měl přednášku na 80. sjezdu německých přírodovědců a lékařů v Kolíne nad Rýnem s názvem Raum und Zeit. V ní vysvětlil, jak lze přehledně zapsat závěry speciální teorie relativity a jak lze geometricky interpretovat Lorentzovou transformaci. Albert Einstein z toho nadšen nebyl. Důvody byly dva. První spočíval v tom, že nebyl až tak silný v matematice, nakonec i proto se celý život obklopoval vynikajícími matematiky, kteří mu pomáhali převést do matematické podoby jeho geniální fyzikální myšlenky. Nakonec proč ne, člověk nemůže znát vše. Druhý důvod měl původ v opatrnosti, věděl, že matematici mají tendenci vše formalizovat, podstatu utopit v přesných důkazech, což nejednou vede k tomu, že vlastní obsah sdělení se ztrácí kdesi v mlze. Naštěstí čas ukázal, že v případě Hermanna Minkowského Albert Einstein pravdu neměl. Jeho myšlenky významnou měrou přispěly k smysluplné a velice názorné geometrické interpretaci Lorentzovy transformace i důsledků speciální teorie relativity.
Říká se, že na internetu člověk najde vše. Pravda to není ani zdaleka, ale přesto jsem až udiven, že na českých internetových stránkách neprofesionální zájemce nenajde srozumitelný výklad myšlenek Minkowského prostoročasu s důrazem na jejich geometrickou interpretaci. Tak jsem si řekl: Nekritizuj, napiš a lapidárně pro laiky vylož! Pokud můj výklad nebude dostatečně přesný a jasný, částečně mě omlouvá to, že nejsem ani fyzik, ani matematik, ani učitel, nejspíš budu něco jako laik se širším rozhledem, který jednou za uherský rok sáhne po nějaké knize z matematiky nebo fyziky. Popravdě poslední roky již ani ne za ten uherský rok. Důvody jsou dva: věk a oči.
Než se pustím do vlastního výkladu tři technické poznámky. Pokud se budu odvolávat na číslo obrázku, číslo zjistíte po najetí myší na obrázek. Jelikož v jazyce HTML beze změny fontu písma (což nechci dělat) nejde psát řecká písmena, tak tam, kde to bude nezbytné, použiju v textu slovní vyjádření řeckého písmena. Konkrétně to budou písmena: tau, beta a ný. Tau je ekvivalentní tc, beta výrazu V/c a ný úhlu v Minkovského prostoročase, který svírají osy x a x’ a ct a ct’. No a do třetice vysvětelení k mému volně psanému textu a malůvkám od ruky. K nakreslení dvou obrázků s rastrem v pozadí jsem použil volně dostupný webový program www.meta-calculator.com. Pak mě to již přestalo bavit a zbývající obrázky jsem nakreslil, částečně i načmáral, pravítkem a volnou rukou. Snad to většina čtenářů v době, kdy nejednou forma je více než podstata, unese.
Z fyziky předpokládám u čtenáře pochopení Lorentzovy transformace a znalost faktu invariantnosti prostoročasového intervalu. Pro čtenářovo pohodlí kvantitativní rekapitulace je uvedena na obrázku č. 1. Abych se i sám trochu procvičil v algebře, připojil jsem i důkaz invariantnosti prostoročasového intervalu. Indexy 1 a 2 označují dva světobody v prostoročasu. Světobod je definován místem a časem. V světobodu se může, ale nemusí, udát nějaká událost. Nakonec i v našem životě se vše odehrává vždy v nějakém konkrétním místě a v nějakém konkrétním čase. Jedno možné odvození Lorentzovy transformaci je např. v mém textu na těchto webových stránkách. V jiném textu jsem popsal, jak elegantně lze Lorentzovu transformaci vyjádřit pomocí hyperbolických funkcí, ale tyto funkce v tomto textu nebudeme používat.

Malá poznámka k Lorentzově transformaci. Pozorný čtenář si jistě všimnul, že jsem zapomněl připsat transformační rovnici y’ = y, potažmo v prostoru z’ = z, tedy že kolmo na směr pohybu se žádná transforamce neděje. Má pravdu. Jenom připomenu, že pokud by se ve směru osy x v rovině pohybovala tyč, která by v soustavě spojené s tyčí s osou x svírala úhel různý od nuly, tak v důsledku Lorentzovy transformace by se z pohledu soustavy, z které pohyb tyče pozorujeme, tento úhel změnil, konkrétně byl by větší. Proč? Protože v důsledku kontrakce se x-ový rozměr tyče zmenší a y-ový zůstane stejný (y’ = y). Pokud čtenář tehle poznámce neporozuměl, nic se neděje, pro náš další výklad její nepochopení nemá žádný fatální dopad. V životě jsou horší věci.
Něco málo k literatuře. Knih o speciální teorii relativity, či už dobrých nebo průměrných anebo vyloženě nedobrých je dost. Začátečníkovi bych vřele doporučil nepůvodní slovenský titul Fyzika priestoročasu, úvod do špeciálnej teórie relativity, autorů Edwina F. Taylora a Johna Archibalda Wheelera. Vydala Enigma, 2012. Pro pokročilejší původní český titul Základy speciální teorie relativity. Autorem je Václav Votruba, první vydání vyšlo v nakladatelství Academia Praha v roce 1969, druhé v roce 1977.
Dále z fyziky plně akceptujeme základní předpoklad, že fyzikální děje by měly probíhat ve všech vztažných soustavách stejně. Vztažná soustava je soustava, vzhledem k jejíž počátku měříme souřadnice a čas konkrétního fyzikálního děje neboli trvání jakékoliv události. Nás budou v tomto textu zajímat pouze inerciální soustavy. Je to ideální vztažná soustava, v níž nepůsobí gravitace a jakékoliv těleso v klidu popřípadě v pohybu setrvá v tomto původním stave trvale, aniž by změnilo směr nebo velikost své rychlosti. Uznáte, že by asi nebylo pro nás moc dobré, kdyby pro pozorovatele v soustavě spojené se Zemí probíhaly fyzikální děje jinak než na nějaké jiné obydlené planetě. To bychom měli více světů, než zvládnou spisovatelé sci-fi. Raději si vystačíme s jedním jediným. Rovněž víme, že rychlost světla c ve vakuu je ve všech inerciálních soustavách konstantní. Tedy je úplně jedno, zda zdroj světla se pohybuje rychlostí 100 000 km/s nebo stojí, stále naměříme stejnou rychlost světla c. Není to intelektuální výmysl, tuhle skutečnost potvrzuje řada velice přesných fyzikálních experimentů.

Pokud jde o matematiku bohatě vystačíme s látkou ze střední školy. Čtenář bude z geometrie potřebovat pouze znalost analytického zápisu rovnice hyperboly v tom nejjednodušším tvaru a zápis rovnice přímky vycházející z počátku v tzv. směrnicovém tvaru. Vše je vidět na obrázcích č. 2 a č. 3 s rastrem v pozadí. Pokud jde o hyperbolu na obrázku č. 2 vidíme dvě jednotkové hyperboly: x2 – y2 = 1 a y2 – x2 = 1. Doporučuji čtenáři, aby si je sám s tužkou a kalkulačkou v ruce nakreslil. Já to učinil také. Na obrázku jsou zakresleny i asymptoty obou hyperbol: y = x a y = -x. K těm se hyperbola pouze přibližuje, ale nikdy se jich nedotkne. Jejich rovnice se lehce odvodí malým trikem, vypočtou se z rovnic x2 – y2 = 0 nebo y2 – x2 = 0.

Pokud jde o přímku, snad je vše jasné (látka ze základky). Text má i malý matematický dodatek, pokud jej bude chtít čtenář pochopit, potřebuje něco málo znát ze základů analytické geometrie a vyřešit jednoduchou soustavu dvou rovnic o dvou neznámých. Dodatek jsem zařadil pouze proto, že chci ukázat, jak jsou výpočty v Minkowského protoročasu přirozené a relativně jednoduché. Kromě tohoto dodatku se budeme pobybovat jen a jen na půdě geometrie, tedy budeme kreslit. Z již zmíněného slavného článku Raum und Zeit jsem pořídil malý výsek, viz obrázek č. 4. Zde Hermann Minkowski názorně ukázal, jak lze geometricky interpretovat Lorentzovou transformaci, a tím i její důsledky. Text kolem obrázku a samotný obrázek nás budou doprovázet po celou dobu výkladu. Pokud umíte německy a porozumíte koncentrovanému matematickému textu a pochopíte to, co je obrázkem sděleno, již je zbytečné dále tento text číst, byla by to pro vás jenom ztráta času. Pokud ne, nezoufejte a pokračujte ve čtení.

Abychom výklad zbytečně nekomplikovali – což umí hlavně ti, kteří tomu, co vykládají, příliš nerozumí – vše si ukážeme v rovině, nakonec i Hermann Minkowski na obrázku uvažuje časovou a jenom jednu prostorovou souřadnici. Přechod do čtyřrozměrného prostoru: tři prostorové souřadnice a jedna časová, je pak již relativně jednoduchý.
Naším prvním krokem bude nakreslení Minkowského prostoročasu v rovině, tedy na obyčejnou čtvrtku papíru tužkou a pravítkem. Mějme dvě inerciální soustavy, z nichž jedna se vůči té druhé pohybuje rychlostí V. Tu v relativním klidu si označíme K, tu druhou, která se vůči ní pohybuje rychlostí V písmenem s apostrofem K’. Situaci si můžeme názorně představit tak, že my se nacházíme v první soustavě (jsme v relativním klidu) a ta druhá se vůči nám pohybuje zmíněnou rychlostí V ve směru osy x. Podívejte se na obrázek č. 5. Zatím si budeme všímat pouze souřadnicové soustavy x, ct, jejíž osy svírají pravý uhel, ta je nakreslena plnou čarou v prvním kvadrantu. Nic ostatního si nevšímejte. Souřadnici ct (v obrázcích řecké písmeno tau) místo pouhého času t používáme proto, že tímto formálním trikem si zajistíme, že na obě souřadnicové osy budeme moci vynášet jednotky délky. Rychlost × čas = vzdálenost, a jak známo, vzdálenost měříme v jednotkách délky. Malé rozšíření pro ty, co znají komplexní čísla: Často se používá místo součinu ct součin ict, kde i je imaginární jednotka. Kvadrát časové souřadnice ve vzorci pro interval pak je -c2t2, jelikož i2 = -1. Interval se pak zapisuje ve tvaru x2 - c2t2 a pojmenování prostorovočasový interval má pak větší logiku než v našem zápisu intervalu c2t2 - x2. V našem případě bychom spíš měli mluvit o časoprostoru, když časová souřadnice vystupuje v zápisu intervalu jako první. Autor tohoto textu si je téhle nedůslednosti vědom, ale líbí se mi německé spojení Raum und Zeit, tak používám raději pojmenování prostoročas bez ohledu na tvar intervalu. Ve finále je to ještě vše o něco složitější, viz náznak popisu téhle složitosti v druhém odstavci textu za obrázkem č. 7. Bodům v Minkowského prostoročasu budeme říkat světobody, abychom zdůraznili skutečnost, že světobod je určen místem a časem.
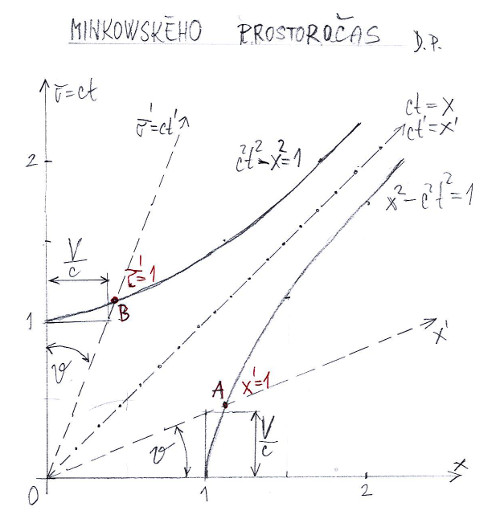
Co můžeme ze souřadnicové soustavy x, ct hned vyčíst? Především, že počátek má souřadnice x = 0 a ct = 0. Pokud si na ose x vyznačíme libovolné dva světobody, v kterých se např. něco událo (ale nemuselo se), hned vidíme, že události se se sice udály na různých místech, ale v stejném čase ct = 0, někdy říkáme, že události se udály současně. Pokud si podobné dva světobody nakreslíme na ose ct, hned vidíme, že události se v nich udály ve dvou různých časech, ale na stejném místě, v tomto případě v počátku. O takových událostech říkáme, že jsou soumístné. Pokud si nakreslíme libovolný světobod, z obrázku umíme zjistit jeho prostorovou a časovou souřadnici.
V Minkowského prostoročasu každý světobod či událost má svou světočáru (analogie historie života člověka). Jako příklad si teď zkusme do vztažné soustavy x, ct nakreslit světočáru pohybu světla. Jelikož rychlost světla je obrovská, ať na ose x jednotka délky je právě rychlost světla, tedy 1 odpovídá 1c, 2 odpovídá 2c atd. Světelný paprsek vypustíme z počátku, tedy ze světobodu ct = 0, x = 0. Kam doletí za 1 sekundu? Přesně do vzdálenosti 1c, což odpovídá na ose x souřadnici 1. Přímky x = 1 a ct =1 se protnou ve svetobodě x = 1, ct = 1. Za dvě sekundy světlo dorazí do bodu x = 2, ct = 2. Dále jistě není potřeba pokračovat, světočárou pohybu světla je přímka procházející počátkem pod úhlem 45°. Rovnice téhle přímky v soustavě K je ct = x, protože směrnice k je 1. Stačí si vzpomenout na rovnici přímky ve směrnicovém tvaru: y = kx, z které dostaneme k = y/x. V případě světla y = ct a x = ct, což dává k = 1, no a tg 45° = 1. Všimněme si, že hodnota intervalu ve všech bodech světočáry světla vyslaného z počátku souřadnicové soustavy je nulová.
Jaké budou světočáry koncových světobodů pevné tyče, kterou někdo umístil kdekoliv na osu x a již nic se s ní neděje. Budou to dvě rovnoběžky s osou ct vedené počátečním a koncovým světobodem pevné tyče. Proč? No proto, že ta tyč tam leží a bude ležet, bez ohledu na to, jaký čas uplynul a uplyne. Pokud by s tyčí začal někdo pohybovat, byly by to obecně dvě křivky zachycující polohu začátku a konce tyče v prostoročase. Co za světočáru je osa tc? Je to světočára všech světobodů se souřadnicí x = 0, tedy vše, co se odehrálo v počátku souřadnicového počátku a také odehraje, jak půjde čas. Co za světočáru je osa x? Je to světočára všech světobodů se souřadnicí tc = 0, tedy vše, co se odehrálo ve všech světobodech na ose x právě v okamžiku tc = 0.
Zakreslení souřadnicové soustavy K jsme zvládli, rovněž zakreslení světočáry světla. Teď stojíme před náročnějším úkolem: zakreslit do Minkowského prostoročasu soustavu K’, která se vůči soustavě K pohybuje rychlostí V ve směru osy x. Naším cílem bude nalezení rovnic os x’ a ct’ v soustavě K. Čeho se chytit? Tady je odpověď jednoduchá, budeme vycházet z Lorentzovy transformace. Celý výpočet vidíte na obrázku č. 6. Vlastní zakreslení os x’ a ct’ je zřejmé z předchozího obrázku č. 5.

Zvládli jsme již zakreslení Minkowského prostoročasu? Ne, protože v teorii relativity je opravdu vše relativní. Vše jsme kreslili z pohledu soustavy K, ale v teorii relativity soustava K nemá žádné výsadní postavení vůči soustavě K’, ta je stejně fyzikálně dobrá. Jak by Minkowského prostoročas vypadal z pohledu soustavy K’? Vzpomeňme si na vizuální pocit, který máme při pohledu z okna při rozjedu vlaku ze stanice z nástupiště, kde na protilehlé koleji stojí vlak. Chvíli nevíme, zda se vlak nerozjíždí přesně opačným směrem, než je náš směr. Po chvilce si uvědomíme, to již zafunguje rozum, že se rozjel náš vlak a že druhý vlak stojí. Podobná situace je se soustavou K’. Z jejího pohledu v Minkowkého prostoročasu budou pravoúhlé souřadnice tvořit osy x’ a ct’. Soustava K bude ujíždět opačným směrem, než tomu bylo v případě soustavy K’. Jak tuhle skutečnost zohledníme na obrázku? Velice jednoduše: úhly ný vyneseme opačnými směry, takže souřadnicová soustava K bude kosoúhlá s tupým úhlem. Na našem obrázku č. 4 souřadnicová soustava K’ je kosoúhlá s ostrým úhlem 90° - 2.ný. Úhel kosoúhlosti je tím ostřejší, tedy menší, čím je rychlost soustavy K’ větší. Při malých rychlostech souřadnicové soustavy K a K’ téměř splývají, i to ukazuje, že Hermann Minkowski geometrii Lorentzovy transformace vymyslel dobře. Víme, že při malých rychlostech V Lorentzova transformace přechází do klasické Galileiho transformace, jelikož poměr V/c (v literatuře se vesměs značí řeckým písmenem beta) je zanedbatelný. Snad nebude od věci připomenout, že v Galileiho transformaci čas je absolutní, tedy v obou soustavách t = t’. Proto v geometrickém zobrazení Galileiho transformace se časová osa nevynáší, je to zbytečné, jelikož stačí napsat transformační vzorec pro čas ve tvaru t’ = t. V Galileiho transformaci si vystačíme pouze s transformací prostorových souřadnic.
Položme si opět stejnou otázku: Zvládli jsme již zakreslení Minkowského prostoročasu? Odpověď bude bohužel opět záporná, jelikož osy x’ a ct’ musíme kalibrovat, tedy určit v této soustavě velikost jednodky vzdálenosti a času. V Galileiho transformaci nás tyhle věci netrápili, tam jednotky času i vzdálenosti jsou v obou soustavách stejné. Opět se musíme chytit něčeho, co je pro obě soustavy stejné, tomu stejnému v různých soustavách říkáme učeně invariant. Jistě, máte pravdu, na obrázku č. 1 jsme si dokázali invariantnost prostoročasového intervalu. Ovšem ten, když se má zachovat, musí to fungovat tak, že pokud nám vyjde delší jednotka délky v soustavě K’ (zatím uvažujeme jenom teoreticky) než v K, musí vyjít větší i jednotka času, jelikož pak by se nerovnaly prostoročasové intervaly v K a K’. Na dalším obrázku, má č. 7, máte vysvětleno jak se taková kalibrace dělá geometricky. V bodě č. 1 tohoto obrázku je přípravná úvaha, která vysvětluje proč jednou používáme zápis s2 = c2t2 - x2 a podruhé s2 = x2 - c2t2. Má to i hlubší fyzikální zdůvodnění, ale abychom výklad zbytečně nenatahovali (beztak je dlouhý až až), spokojíme se s matematickým zdůvodněním. V oblasti 2 (je v kroužku) by nám interval vyšel záporný a jak víme, výpočet odmocniny ze záporného čísla vede k tzv. imaginárním číslům. Téhle nepříjemnosti jsme se zbavili velice jednoduše, vynásobením obou stran rovnosti číslem -1, což zakázáno není.

Teď se konečně můžeme vrátit k obrázku č. 5, kde vidíme způsob určení světobodů A a B, jejichž vzdálenost od počátku souřadnicového systému definuje velikost jednotek délky a času. Tím je konstrukce Minkowského časoprostotu úplná.
Pro milovníky výpočtů a analytické geometrie jsem do doplňku zařadil výpočet velikosti jednotky času a délky. Ve skutečnosti je výpočet proveden pouze pro výpočet velikosti jednotky délky, ale z obrázku č. 5 již pouhým pohledem vidíme, že výpočet velikosti jednotky času by byl téměř stejný a dopracovali bychom se k stejnému výsledku. Nakonec tahle kvantitativní rovnost má svou logiku zabudovanou v samotném tvaru intervalu s’2 = c2t’2 - x’2. Když se zvětší hodnota prvního členu o nějakou hodnotu, musí se druhá hodnota zvětšit o stejnou hodnotu, aby rozdíl dal stejnou hodnotu jako je s2. Kvalitativně stejnost spočívá v tom, že prostoročas tvoří jednotu prostoru a času. V oblastech, kde je větší časový člen intervalu c2t2 než prostorový x2, mluvíme o časopodobné oblasti, tam kde je větší prostorový člen intervalu než časový mluvíme o prostoropodobné oblasti. Je dobré si uvědomit, že nad světočarou světla je v každém světobodě časová souřadnice větší než prostorová. Kupříkladu nech časová souřadnice je 1 a prostorová 0,25 a spojme tento bod s počátkem. Dostali jsme světočáru tělesa, které se pohybuje rychlostí c/4. Proč? Protože za 1 sekundu urazilo vzdálenost 0,25.300 000 km/s. Teď si spojme s počátkem bod, jehož časová souřadnice je 0,25 a prostorová 1. Co je to za světočáru? Velice zajímavá, tohle těleso by se mělo pohybovat rychlostí 4c, jelikož za 0,25 sekundy urazilo vzdálenost 300 000 km. Ovšem víme, že to není možné, nic se nemůže pohybovat rychleji než je rychlost světla c. Proto světočára zakreslená pod světočarou světla nemá reálný fyzikální význam. Maximálně mohu uvažovat takhle: Aha, ve vzdálenosti 300 000 km se něco stalo, kupříkladu nastal tam světelný výbuch, ovšem já se tenhle fakt dozvím až za 1 sekundu, protože tolik světlo potřebuje na uražení vzdálenosti 300 000 km.
Pokud geometrická interpetace Lorentzovy transformace v podobě, kterou jsme si vysvětlili, má mít u fyziků úspěch, musí být pomocí ní přirozeně a pokud možno lehce interpretovalné i důsledky plynoucí z Lorentzovy transforamce, konstantní rychlosti světla a rovnocennosti všech inerciálních soustav. Nejznámější a nejvíce uváděné důsledky jsou tři: relativnost současnoti, kontrakce délky a dilatace času. Lze se k ním dopracovat jednoduchým výpočtem využitím Lorentzovy transformace, tyhle výpočty uvádí snad každá podrobnější učebnice fyziky, proto je zde vypouštím. My si je odvodíme geometrickou metodou v Minkowského prostoročasu. Současně se tím potrénujeme v zakreslování světočár. Doporučuji si každý obrázek nakreslit volně rukou a doprovázet vlastním komentářem s důrazem na význam každé světočáry a každého světobodu. Ve fyzice, na rozdíl např. od matematiky, nestačí se dopracovat k správnému výsledku, neméně důležitá je správná fyzikální interpretace výsledku. Humanitní vědy jsou na tom často ještě lépe, stačí se podívat z okna a vymyslet nějakou teorii a pak realitu šikovně interpretovat tak, aby zapadla do teorie, viz např. Karel Marx nebo Sigmund Freud. V takových případech mluvíme o absenci kritického myšlení vůči vlastní teorii. Právě přístup Alberta Einsteina při vytváření speciální i obecné teorie relativity je vzorovou ukázkou kritického myšlení.
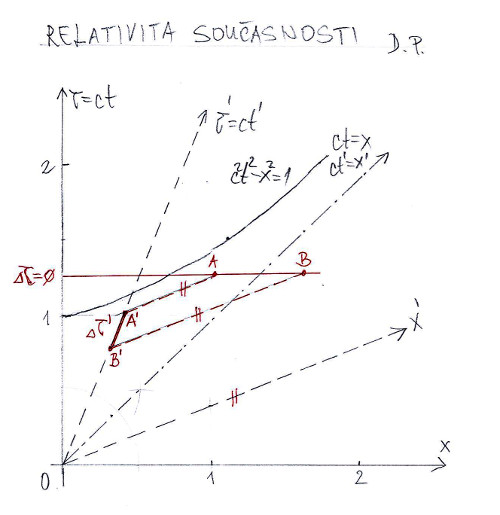
Relativnost současnosti událostí
Nikde není dáno, že pokud se udály v soustavě K dvě události v různých světobodech A, B ve stejném čase (současně), že se musely udát ve stejném čase i v soustavě K’. Vysvětlení je zřejmé z obrázku č. 8. Stejně to musí fungovat z pohledu soustavy K’. Tuhle situaci jsem do obrázku nezakreslil kvůli přehlednosti. Zkuste si to sami, uvidíte, že to dopadne stejně.
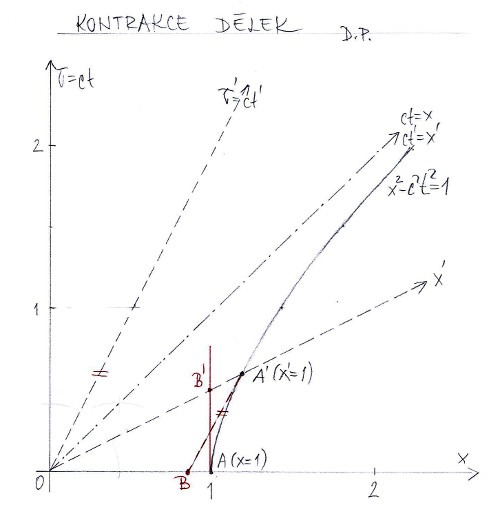
Kontrakce délky pevných těles
Nikde není dáno, že pokud má pevné těleso v soustavě K’ určitou délku (obvykle jí říkáme vlastní délka), že má stejnou délku i z pohledu relativně klidové soustavy K. Přitom nesmíme zapomenout, že délku měříme v jednotkách délky příslušné soustavy, jelikož už víme, že tyhle jednotky nejsou v obou soustavách stejné, pouze při malých rychlostech V jsou skoro stejné. Kdyby kontrakce nebyla, tak jednotková pevná tyč by měla v soustavě K jednotkovou délku OA a v soustavě K’ délku OA’. Ale z obrázku jasně vidíme, že tomu tak není. Z pohledu soustavy K délka jednotkové pevné tyče v soustavě K’ má velikost OB’, tedy je kratší než jednotková délka OA’. Z pohledu soustavy K’ to dopadne stejně. Místo délky OA, pevná tyč má délku OB.
Dilatace času
Nikde není dáno, že pokud v soustavě K’ uplyne mezi dvěma událostmi určitá doba (obvykle této době říkáme vlastní doba trvání), že z pohledu relativně klidové soustavy K uplyne stejně dlouhá doba. Opět nesmíme zapomenout, že délku doby trvání měříme v jednotkách času příslušné soustavy, jelikož už víme, že ani jednotky času nejsou v obou soustavách stejně veliké, pouze při malých rychlostech V jsou skoro stejné. Kdyby k žádné dilataci času nedocházelo, tak jednotka délky času by měla v soustavě K jednotkovou délku OA a v soustavě K’ délku OA’. Ale z obrázku vidíme, že tomu tak není. Z pohledu soustavy K délka jednotky času v soustavě K’ má velikost OB’, tedy je kratší než původní jednotková délka OA’, tedy v soustavě K již jednotka času uplynula, ale v soustavě K’ ještě ne, neboli v soustavě K se žije rychleji než v soustavě K’. Z pohledu soustavy K’ to dopadne naprosto stejně. Místo délky jednotky času OA má jednotka času velikost OB. Tedy z pohledu soustavy K’ již uplynula jedna jednotka času, ale v soustavě K ještě ne, neboli v soustavě K’ se žije rychleji než v soustavě K.

Pokud se o speciální teorii budete zajímat více a budete si počítat i nějaké příklady, neopomente ověřit výsledek z pohledu obou soustav. Nakonec v našem výkladu jsme postupovali stejně. Když něco platilo z pohledu soustavy K, ukázali jsme, že to stejné platí z pohledu soustavy K’. V reálném životě tomu tak často není. Pokud najde stokorunovou bankovku bezdomovec, potěší ho to s velikou pravděpodobností hodně, jelikož je to pro něj dost peněz. Pokud ji najde miliardář, sice ho to potěší také, ale pravděpodobně ne tolik, kolik bezdomovce, jelikož pro něj sto korun až tolik moc peněz není. A to je vše.
Doplněk. Ukázka analytického výpočtu jednotky délky a času v soustavě K’ v Minkowského prostoročasu. Výpočet je ve skutečnosti proveden pouze pro výpočet jednotky délky vzdálenosti, ale pro výpočet jednotky času je zcela analogický, rovněž výsledek je stejný. Proč? Jelikož v Minkowského prostororočase jsou čas a prostor symetrické, viz obrázek č. 5.

V Brně ve dnech 23. srpna až 4. září 2017. Publikováno 5. září 2017.