Hyperbolický sinus a kosinus
Dušan Polanský
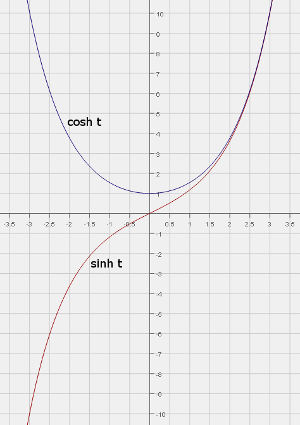
Pro populární matematické povídání jsem tentokráte zvolil o něco složitější námět než obvykle. Ukážeme si, že podobně jak lze zavést trigonometrické funkce pomocí jednotkové kružnice, tak lze zavést velmi podobně i hyperbolické funkce pomocí jednotkové hyperboly. Z hyperbolických funkcí se zaměříme hlavně na hyperbolický sinus a kosinus. V zvolené ukázce aplikace těchto funkcí ve fyzice je použit i hyperbolický tangens, ale znalost jeho průběhu nebudeme potřebovat. Na obrázku č. 1 je pro základní představu vykreslen průběh hyperbolického sinu a kosinu. Protože obě funkce prudce stoupají a klesají na ose x jsou stupně. Definiční obor je u obou funkcí od mínus do plus nekonečna. Obor hodnot je u cosh t [1, + nekonečno], u sinh t [- nekonečno, + nekonečno]. Hned zde vidíme rozdíl oproti funkcím trigonometrickým, hyperbolické funkce nejsou periodické. Pokud bychom ale opustili svět reálných čísel a vydali se do světa čísel komplexních, tam již periodické jsou. Ukážeme si i některé další analogie mezi trigonometrickými a hyperbolickými funkcemi.
Pro některé důkazy uvedené v dodatcích je potřebná znalost základů diferenciálního a integrálního počtu, jinak ale vystačíme s běžnou středoškolskou matematikou. Takže pokud důkazům uvedeným v dodatcích uvěříte, tak se obejděte i bez znalosti diferenciálního a integrálního počtu. To, co je nezbytné znát pro pochopení výkladu je uvedeno na obrázku č. 2. Jedná se o připomenutí definice radiánu coby jednotky obloukové míry a pak některých elementárních vlastností hyperboly. Pro další výklad budeme potřebovat ještě vzoreček pro obsah kruhové výseče jednotkové kružnice a základní znalosti o jednotkové hyperbole a jejím průběhu.
Jedna technická poznámka. Jelikož v jazyce HTML beze změny fontu písma (což nechci dělat) nejde psát řecká písmena, jimiž označujeme dle našeho zvyku úhly, tak zápis úhlu v textu občas nějak kostrbatě ošidíme, obvykle ale úhel budeme označovat písmenem t. Druhou odmocninu obvykle píšeme zkratkou sqrt.
Pro nakreslení obrázků s rastrem v pozadí jsem použil volně dostupný webový program www.meta-calculator.com. Texty v obrázcích jsem doplnil volně dostupným programem GIMP. Čísla obrázků, dost se na ně v textu odvolávám, lze zjistit po přesunu myši na příslušný obrázek.

Začneme trocha zeširoka, abychom získali jakýs takýs nadhled nad celou problematikou. Ovšem jenom u nadhledu nezůstaneme, jak to mnozí autoři s oblibou činí s odvoláním se na složitost řešené problematiky, hned poté se vnoříme do detailů.
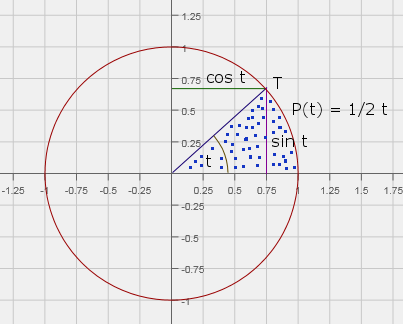
Na základní škole jsme se v geometrii učili o trigonometrických funkcích: sin t, cos t, tan x (často také tg t), cotan t (často také cotg t). Zaváděli se a vysvětlovali pomocí pravoúhlého trojúhelníku. Ještě nám paní učitelka, ta moje byla velice nepříjemná a matematiku neuměla vyložit, odvodila z pravoúhlého trojúhelníku pomocí Pythagorovy věty vztah cos2 t + sin2 t = 1, což není nic jiného než zápis rovnice jednotkové kružnice, pro kterou platí: r = 1. Z toho také hned plyne, že bod T(cost, sint) leží na kružnici x2 + y2 = 1, viz obrázek č. 3. Na první pohled je vidět, že trigonometrické funkce jsou opravdu úzce svázány s pravoúhlým trojúhelníkem a křivkou zvanou jednotková kružnice. Na obrázku je tečkovaně vyznačena kruhová výseč se středovým úhlem t.
Na střední škole se člověk dozví, že mezi trigonometrickými funkcemi existují další, více či méně rafinované, vztahy. Stejně, pokud si je člověk neumí odvodit, tak je spolehlivě zapomene, takže se toho moc nového nedozví. V mém případě k matematice na stavební průmyslovce patří vzpomínka na vzteklého starého matematika, který mi matematiku málem definitivně zhnusil, čímž plynule navázal na dílo paní učitelky ze základní školy. Jenomže když to ve vás je, tak to tam je. To máte jako s kouřením či alkoholem nebo sklonem k lumpárnám.
Na vysoké škole se trigonometrické funkce v matematice používají především při výpočtech integrálů a diferenciálních rovnic. Ovšem každý autor vysokoškolské učebnice matematiky či diferenciálního a integrálního počtu neopomene uvést, že abychom si my, banda jedna nevzdělaná, nemysleli, že trigonometrické funkce jsou nějak výjimečné, že jsou i další funkce, např. hyperbolické, eliptické, Besselovy, Hankelovy, které nejsou o nic složitější než zmíněné funkce trigonometrické, ale jelikož se tak často v praxi nepoužívají, tak proto jim není věnována taková pozornost jako funkcím trigonometrickým. O pravdivosti téhle úvahy lze diskutovat, ale já jsem zvolil jiný přístup. V dalším si ukážeme jeden možný přístup (bude silně formální) k zavedení hyperbolických funkcí i malou ukázku jejich využití. Tím vytvoříme čtenáři jakýs takýs prostor, aby si sám udělal názor na složitost a analogičnost těchto funkcí vůči trigonometrickým funkcím. Pro vyspělejší čtenáře dodávám, že zavedení zmíněných Besselových a Hankelových funkcí je již podstatně složitější, jelikož se obvykle zavádí pomocí řešení speciální diferenciální rovnice v komplexním oboru. Ale nestrašme, tzv. sférické Besselovy a Hankelovy funkce lze zavést i pomocí nám již známých trigonometrických funkcí. Třebaže průběhy těchto exotických funkcí jsou o dost složitější než funkcí trigonometrických, jsou to ale stále jejich potomci. Osobně na výuku matematiky na vysoké škole v Žilině vzpomínám docela rád. Přednášel nám ji starší pán, vášnivý sportovec, odborný asistent Sýkora, který sice hvězdný matematik nebyl, ale uměl látku vyložit a hlavně matematiku studentům neotrávil, což by mělo být hlavním posláním každého učitele, bez ohledu na to, který předmět učí.
Teď když již máme jakýs takýs nadhled můžeme přistoupíme k definici hyperbolických funkcí. Definice jsou silně formální, to proto, že jejich neformální zavedení je poměrně pracné, museli bychom nejdříve spočíst poměrně složité integrály a z jejich výsledků odvodit níže uvedené vzorce. Z nebe padlé definice jsou uvedeny na obrázku č. 4 pod bodem č. 1. Podle těchto definicí byly první dvě funkce zadány i do zmíněného kalkulátoru pro vykreslení jejich průběhu na obrázku č. 1.

Výpočet jejich konkrétních hodnot umí každá slušnější kalkulačka. Zkuste si několik hodnost vypočíst na kalkulačce a porovnat je s obrázkem č.1, také nezapomeňte ověřit, že cosh 0 = 1 a sinh 0 = 0. Při výpočtech si je potřeba dávat pozor, zda jejich hodnoty zjišťujeme pro úhly zadané v stupních nebo v radiánech.
Na obrázku č. 3 je v bodě č. 2 dokázán i důležitý vztah cosh2 t – sinht2 = 1. Jeho značná podobnost se vztahem cos2 t + sin2t = 1 bije přímo do očí. Na obrázku č. 2 je pro jednotkovou kružnici uveden důkaz vzorce pro výpočet obsahu kruhové výseče: P(t) = 1/2t, kde t je úhel v radiánech; speciálně z toho plyne, že P(0) = 0. Je možné, že takové vztahy platí i pro jednotkovou hyperbolu, pak by analogie byla značná. Důkaz toho, že tomu tak je, jsem přesunul do dodatku, jelikož důkaz využívá i znalosti z matematické analýzy, což nemusí být pro každého čtenáře znalost běžná. V každém případě důkaz nám říká, že hodnoty hyperbolických funkcí lze zjišťovat z jednotkové hyperboly. Vše vidíme na obrázku č. 5.
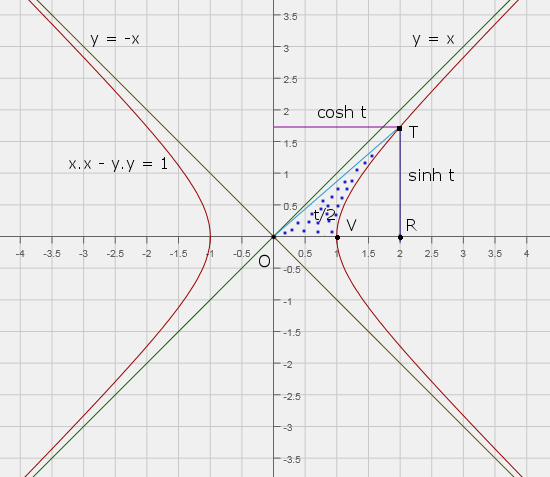
Zde je detailně vykreslená jednotková hyperbola, její asymptoty a rovněž je tečkovaně vyznačena oblast, analogická kruhové výsečy jednotkové kružnice, jejíž plocha je rovněž jako u kružnice: P(t)= 1/2t (důkaz viz dodatek). Také jsou zobrazeny hodnoty cosh t a sinh t pro bod T. Prostě vše jako u kružnice, jenom tady bod T leží na hyperbole. Dokonce i sinh t, podobně jako sin t, se odečítá na vertikále a cosh t, podobně jako cos t, na vodorovné ose. Vidíme, že pomocí jednotkové hyperboly lze námi zkoumané funkce zavést stejně tak dobře, jako podle definice na obrázku č. 4.
Otázkou je, jak z jednotkové hyperboly odečítat hodnoty hyperbolických funkcí? Když se podíváme na obrázek č. 5, tak pro cosh t (2) nám vychází velikost sinh t cca 1,75. Ale pro jaký úhel jsou to hodnoty hyperbolických funkcí? Podle definice spočteme cosh t + sinh t, zjistíme, že součet je roven et. Neboli zapsáno jinak x + y = et. Tuhle rovnici umíme řešit: t = ln (x + y), kde t je úhel. Hodnoty x a y jsou svázány vztahem x2 - y2 = 1, což je rovnice hyperboly. Vše si ukážeme na jednoduchém příkladu. Zvolme si x = 2, z rovnice hyperboly nám pak vychází y = odmocnina z 3, což je 1,73205, tak nějak je to i na obrázku č. 5. Teď spočteme ln (x + y) = ln (2 + 1,73205) = ln (3,73205) = 1,31695°. Když se podíváme na obrázek č. 1, tak pro tuhle hodnotu úhlu, nám hodnoty cosht a sinh t vychází opravdu 2 a 1,73205. Je zajímavé, že tyhle detaily výpočtu jsem nenašel v žádné vysokoškolské učebnici, zdá se, že ani jeden z autorů se nenámahal výpočet si vyzkoušet. Vidíme, že funkce cosh t a sinh t jsou těsně svázány s funkcí přirozeného logaritmu. Pokud vás to zajíma více, podívejte se na výpočet v dodatku č. 2. Tam je dokázáno, že inverzní funkcí k funkci sinh t je funkce ln (x + sqrt(x2 + 1)). Pro funkci cosh t platí velice podobný vztah: ln (x + sqrt(x2 - 1)).
Analogii mezi hyperbolickými a trigonometrickými funkcemi lze dokumentovat i na podobnosti parametrického vyjádření kružnice a hyperboly. Parametrické vyjádření kružnice s poloměrem a je x = acost, y = asint. Pro hyperbolu platí velice podobné vzorce x = acosht, y = asinht. Důkaz je uveden v doplňku č. 3 na obrázku č. 9. Výpočet integrálu neuvádím, protože je uveden v každé učebnici integrálního počtu.
A to je vlastně málem vše. Abychom ale nebyli suchaři, ukážeme si nějakou aplikaci hyperbolických funkcí. A když už, tak něco hoch. Vybral jsem aplikaci z fyziky, a to konkrétně zápis Lorentzovy transformace (LT) pomocí hyperbolického sinu a kosinu, viz obrázek č. 6.
Pokud nevíte, co to LT je, můžete si přečíst např. moje povídání o LT nebo jenom uvěřit, že LT popisuje vzájemnou transformaci souřadnic a času při přechodu od jedné vztažné soustavy k druhé. Souřadnice jedné soustavy označíme x, t a druhé x´, t´. Ta čárkovaná se pohybuje vůči té nečárkované rychlostí v podél osy x. Dále se předpokládá, že když čárkovaná soustava míjí svým počátkem počátek nečárkované soustavy, tak hodiny v obou soustavách ukazují stejný čas, pro pohodlí čas v obou soustavách budeme měřit od okamžiku t = t´ = 0. Tvar LT je uveden pod bodem 1. V bodě č. 2 je LT zapsána v maticovém tvaru. Pro ty, kteří nemají zkušenost s maticovým počtem, jsme v bodě č. 3 uvedli, jak se z maticového tvaru vrátíme zpět ke klasickému tvaru zápisu LT. Tak či onak matice uvedená v bodě č. 2, je vyznačena červenou pastelkou, v jedné diagonále vykazuje symetrii, jsou tam dvě 1, ale v druhé diagonále symetričnost nám zatím schází, výrazy jsou rozdílné. Podle teorie relativity prostor a čas tvoří jednotu, takže by bylo hezké dopracovat se k takovému zápisu LT, aby i v druhé diagonále zmíněné matice byly stejné výrazy.

Zkusíme zapsat výrazy pro LT v trochu jiném tvaru, a to pro x´ a ct´. Formálně je to jednoduché, výraz pro t´ uvedený v bodě 1 vynásobíme c. Upravený tvar LT je zapsán v bodě 4. A ejhle po převodu do maticového tvaru matice LT vykazuje symetrii i v druhé diagonále. A přesto ještě nejsme spokojeni, vadí nám výraz před maticí. Nebylo by zlé, nějak šikovně jej zaintegrovat do matice, aby zbytečně nekazil celkový dojem. K této integraci využijeme další hyperbolickou funkci hyperbolický tangens (tanh). V našem výkladu jsme se o něm zmínili jenom okrajově, ale uvěříme i bez odvození, že vztahy uvedené pod bodem č. 5 platí. Pro finální zápis ještě zavedeme označení tanh beta = v/c. Náš nový zápis LT v maticovém tvaru v bodě č. 6 vykazuje nádhernou symetrii. Teď snad i ateista uvěří, že prostor a čas stvořený Hospodinem na počátku vší existence tvoří opravdu symetrickou jednotu. Amen.
Dodatek č. 1. Pro čtenáře znalého základů diferenciálního a integrálního počtu jsem přidal důkaz, že také pro jednotkovou hyperbolu platí obdoba vztahů pro jednotkovou kružnici, tj. P(t) = 1/2t a jako zvláštní případ P(0) = 0. Logiku úvahy pro výpočet plochy P(t) si vysvětlíme na obrázku č. 5. Tečkovaná plocha je plocha, jejíž obsah chceme spočíst. Obsah této plochy získáme jako rozdíl trojúhelníka ORT a zakřivené plochy VRT. Plocha VRT je ale integrál od 0 do cosh t, kde integovanou funkcí je funkce odvozena z rovnice hyperboly, tj. odmocnina z výrazu x2–1. Abychom se vyhli výpočtu integrálu, použijeme malou fintu. Nespočteme P(t), ale derivaci tohoto výrazu P(t)´, což je 1/2. Tento postup nám dovolí použít jednoduchou větu integrálního počtu, jejíž důkaz je uveden v bodě 1. Vlastní výpočet, viz bod č. 2, je pak již relativně jednoduchý, relativně proto, že někomu něco jde v životě lehce, jinému těžce; někdo je bohatý, někdo chudobný; někdo je zdravý, někdo nemocný; někdo hezký, někdo ne moc hezký; někdo žije s životní láskou, někdo to štěstí nemá. Ale takový již život je.

Pokud se někomu výpočet obsahu kruhové výseče (viz obrázek č. 3) pomocí středoškolské matematiky zdal příliš jednoduchý, připojil jsem i výpočet pomocí integrálu. Analogie postupu výpočtu na obrázcích č. 7 a č. 7a bije přímo do očí.

Dodatek č. 2. Pro úplnost výkladu uvádím na obrázku č. 8 výpočet inverzní funkce k sinh t. Výpočet pro cosh t je velice podobný. V bodě 1 je připomenutí význam k inverzní funkce k sin t. Tahle fukce se jmenuje arkussinus, psáno arcsin x, arcus je latinsky oblouk. V bodě č. 2 je odvozena inverzní funkce k sinh t. Odvození je vcelku jednoduché, vystačíme se vzorečkem pro řešení kvadratické rovnice, ale jak můžete vidět, až tak triviální není výsledná funkce. Abychom se o správnosti našeho výpočtu přesvědčili, v bodě č. 3 je proveden výpočet k hodnotě 10,0178. Takové divné číslo jsem zvolili proto, že by nám odpovídající úhle měl vyjít 3 stupně. Výsledek je ale o málo jiný. Je to proto, že jsme počítali pouze na 4 desetinná čísla. Porovnejte výsledek s obrázkem č. 1.

Dodatek č. 3. Porovnání parametrického vyjádření kružnice a hyperboly. U parametrického vyjádření jde o to, vyjádřit souřadnice x a y v závislosti na vhodně zvoleném jednom parametru. Obvykle se parametr značí písmenem t. V našem případě je parametr u kružnice i hyperboly zvolen stejně, důvod je nasnadě, chceme dokázat silnou analogii parametrického vyjádření kružnice a hyperboly.

V Brně ve dnech 25. července až 1. srpna 2014.