Příklady na Bayesův vzorec
Dušan Polanský
Náhoda a osud nám někdy splývají v jedno, obvykle tomu ale tak není. Někdy náhoda není až tak velikou náhodou, jak se domníváme, a osud se nám nejednou hodí jako alibi za něco nehezkého, co jsme někomu provedli nebo je výmluvou za naši neschopnost. Přesto vše nás svět náhody přitahuje. Hlavní důvod bude asi v tom, že když se nedaří, nabízí nám alespoň potenciální šanci, že může být v budoucnu lépe. Ale dost mlhavých úvah, které si každý z nás může vyložit, jak se mu hodí do krámu. Raději se necháme pozvat Thomasem Bayesem (asi 1701–1761) anglickým duchovním do světa podmíněné náhody neboli pravděpodobnosti. Vše se bude točit kolem jeho slavného vzorce, který říká, jak podmíněná pravděpodobnost nějakého jevu souvisí s opačnou podmíněnou pravděpodobností. Žádné obavy, vlastní matematické výpočty jsou jednoduché, bohatě vystačíme se čtyřmi základními operacemi v rozsahu základní školy.
O pravděpodobnosti jsem již dříve napsal dva střípky, první úvodní, a pak druhý více specializovaný, ten byl o problému z očního lékařství, na který jsem aplikoval Bayesův vzorec. Několik čtenářů mi napsalo, že mezi těmi dvěma střípky je poměrně veliký skok v náročnosti, že druhý je o dost náročnější než první, že by to chtělo napsat ještě něco mezi tím. To je pávě motivace tohoto textu. Ale aby toho nebylo málo, později, než byl napsán tento střípek, jsem napsal další elementární text o logice výpočtu v rámci bayesovské teorie pravděpodobnosti. Zajímavý příklad je uveden a vyřešen v střípku o šílenci.
Jak budeme postupovat? Nejdříve si vysvětlíme pojem podmíněné pravděpodobnosti, poté si odvodíme vzorce, které budeme při výpočtech potřebovat. Odvození je formální, pokud by vám dělalo problém, stačí si uvědomit význam výsledných vzorců. V další časti vyřešíme jeden příklad na větu o úplné pravděpodobnosti, poté na rozcvičení dva vzorové příklady, pak budou následovat dva příklady na Bayesův vzorec a na samém konci si vysvětlíme a vyřešíme problém Montyho Halla. Tento problém v USA zná každý středoškolák, je tam málem tak populární jako u nás Haškův Dobrý voják Švejk. V později napsaném doplňku na konci texru je uveden ještě jeden příklad. Tři z příkladů, které budeme zde řešit, jsou ze sbírky příkladů A. A. Svešnikov a kol.: Sbírka úloh z teorie pravděpodobnosti, matematické statistiky, a teorie náhodných funkcí, titul vydalo SNTL v Praze v roce 1971. Na tento titul se budeme odvolávat slovem Sbírka. Vybral jsem neřešené příklady, výsledky jsem zkontroloval podle odpovědí a řešení na konci knihy. Je možné, že čtenář najde elegantnější řešení, než jsou ty má. Zde uvedené postupy řešení se neopírají o žádné geniální úvahy, jsou to logické postupy opírající se o použití základních vzorečků a důsledné ujasnění výchozích podmínek a jejich přesný zápis. Vzorové příkaldy nejsou ze Sbírky, první je tak trochu tradiční, lze jej nalézt ve velice podobných obměnách v různé literatuře, zařadil jsem jej jenom z didaktických důvodů. Druhý vzorový příklad jsem převzal z rusky psaného titulu: B. V. Gnedenko, A. Ja. Chinčin: Elementarnoje vedenje v teoriju verojatnostěj, Moskva , 1961. Příklad vysvětlím a rozeberu detailněji než je tomu v knížce. Rovněž jsem částečně přeformuloval zadání a přizpůsobil označení dnešním zvyklostem. Tento příklad je velice poučný a typický na aplikaci Bayesova vzorce.
Pokud jde o vstupní znalosti, předpokládám, že čtenář zvládnul plně první střípek a z druhého rozumí pojmu podmíněná pravděpodobnost. Pro ty čtenáře, kterým by se výklad v druhém střípku zdál zdlouhavý, jsem o něco níže, jak jsem již zmínil, zařadil vysvětlení podmíněné pravděpodobnosti na jednoduchém příkladu. V druhém střípku je podrobně odvozen i Bayesův vzorec. Zde je odvozen obecnějším, ale formálnějším postupem.
Vše o čem si budeme povídat, vychází z definice podmíněné pravděpodobnosti, jak je uvedena na obrázku č. 1 (číslo obrázku zjistíte po najetí myší na obrázek) pod bodem č. 1. Často se tento vzorec uvádí jako definice podmíněné pravděpodobnosti. Zkusme si motivaci k této definici ilustrovat jednoduchým příkladem. Házíme postupně!!! dvěma klasickými hracími kostkami (krychle, pravidelné šestistěny). Ptáme se, jaká je pravděpodobnost, že součet hodnot na obou kostkách bude rovný 7 za podmínky, že na jedné z kostek padlo číslo menší než 3? Povrchně můžeme uvažovat nějak takto. Všech kombinací, které mohou padnout při hodu dvou kostek je 6 × 6 = 36, ale součet 7 může padnout pouze kombinacemi (1,6), (2,5), (3,4), a protože kostky jsou dvě, vyhovují i inverzní kombinace (6,1), (5,2), (4,3), tedy celkem vyhovuje 6 kombinací. Kdyby nebylo podmínky, že na jedné kostce padlo číslo menší než 3, pravděpodobnost padnutí 7 by byla 6/36 = 1/6. Nás ale zajímají pouze kombinace, kdy na jedné kostce padlo číslo menší než 3, do úvahy nakonec přicházejí z výše uvedených kombinací tyto možnosti: (1,6), (2,5), (6,1) (5,2). Podle klasického vzorce pro výpočet pravděpodobnosti je pravděpodobnost 4/36 =1/9. Je to ale opravdu správný výsledek?
Při druhém pokusu o výpočet zkusme být důslednější. Nech jev A je: součet hodnot na obou kostkách je 7. Jev B nech je: na jedné z kostek padlo číslo menší než 3, tedy číslo 1 nebo 2. Nás zajímá P (A | B), což čteme: podmíněná pravděpodobnost jevu A, když nastal jev B. Podmíněná proto, že hledáme pravděpodobnost jevu A, když již dříve nastal jev B! Spočteme nejdříve dvojice, které vyhovují jevu B: (1,1), (1,2), (1,3), (1,4), (1,5), (1,6); (2,1), (2,2), (2,3), (2,4), (2,5), (2,6); (3,1), (3,2); (4,1), (4,2); (5,1), (5,2); (6,1), (6,2). Celkem 20 kombinací. Nás ale zajímají pouze kombinace, při nichž padl součet 7. Jevu A (součet musí být 7) vyhovují z vyjmenovaných kombinací pouze tyto kombinace: (1,6), (6,1), (5,2), (2,5), tedy celkem 4 kombinace. Podle klasické definice pravděpodobnosti výsledek bude 4/20 = 1/5. Zkusme tento konkrétní výpočet zobecnit. V čitateli zlomku 4/20 máme průnik jevů A a B, kdežto ve jmenovateli kombinace příznivé jevu B, a to je právě vzorec č. 1 z obrázku č. 1. Promyslete si, kde jsme při prvním výpočtu udělali (schválně) chybu. Máte pravdu, v prvním řešení jsme neuvažovali časovou posloupnost jevů B a A, obě kostky jsme hodili najednou.

Na obrázku č. 1 je dále uvedena věta o úplné pravděpodobnosti. Písmeno H se obvykle používá pro označení jevů tvořících úplný systém jevů, je to proto, že často těmto jevům říkáme hypotézy.
Teď si společně vyřešíme příklad 6.1. ze Sbírky na úplnou pravděpodobnost.
Mějme dvě partie výrobků po 12 a 10 kusech, přičemž v každé partii je jeden zmetek. Náhodně zvolený výrobek jsme přemístili z první partie do druhé, načež se náhodně vybral výrobek z druhé partie. Určete pravděpodobnost, že z druhé partie byl vytažen zmetek.
Před vlastním řešením si je nutné ujasnit časovou posloupnost jevů a jevy si řádné definovat, tak aby jejich význam pochopila i důchodkyně ze zapadlé vesnice na Šumavě. Jev A: z druhé partie výrobků bude vytažen zmetek. Hypotéza H1: nebyl přemístěn zmetek z první do druhé partie výrobků. Hypotéza H2: zmetek byl přemístěn z první do druhé partie výrobků. Vidíme, že H1 a H2 tvoří úplný systém jevů, jelikož buď nastala H1, nebo H2 a jiná možnost není. Teď již stačí aplikovat větu o úplné pravděpodobnosti. Pro větší názornost si vzorec podrobně rozepíšeme: P (A) = P(H1).P(A|H1) + P(H2).P(A|H2). Jaké jsou hodnoty zde uvedených pravděpodobností? P (H1), pravděpodobnost hypotézy pokud zmetek nebyl přemístěn, je 11/12. Proč? Protože v první partii je jenom jeden zmetek a výrobků je 12. P(H2) je pravděpodobnost, že zmetek bude přemístěn, což dává pravděpodobnost 1/12. Jaká bude P(A|H1), tedy pravděpodobnost jevu A, pokud předtím nebyl přemístěn zmetek z první do druhé partie výrobků? Je to 1/11. Proč? V druhé partii je teď 11 výrobků, protože jeden byl přemístěn z první partie, ovšem v druhé partii je na základě H1 stále jenom jeden zmetek. Jaká bude P(A|H2)? Máte pravdu 2/11, jelikož na základě H2 byl do druhé partie přemístěn zmetek, takže jsou tam 2 zmetky, což pravděpodobnost vytažení zmetku výrazně zvyšuje. Hodnoty dosadíme do vzorečku: P(A) = 11/12.1/11 + 1/12.2/11 = 13/132. Vidíme, že aplikaci věty o úplné pravděpodobnosti jsme společně hravě zvládli.
Na obrázku č. 1 je nakonec pod bodem č. 3 odvozen slavný Bayesův vzorec. Uvádí, jak z podmíněné pravděpodobnosti P(A|Hk) vypočíst opačně podmíněnou pravděpodobnost P(Hk|A). Při odvození jsme jenom šikovně přepsali vzorec uvedený pod č. 1.
Člověk se nejlépe učí na nepraktických příkladech. Nejdříve si uvedeme dva slíbené ukázkové příklady a poté ze Sbírky dva příklady na Bayesův vzorec. Nejprve zadání a řešení prvního ukázkového příkladu, viz obrázek č. 1a. Ten ještě typický bayseovský není.
Obchod odebírá stejný výrobek od dvou výrobců.
Od 1. výrobce odebírá 25 % celkového množství, přitom první jakosti je 90 % výrobků.
Od 2. výrobce odebírá 75 % celkového množství, přitom první jakosti je 70 % výrobků.
Určete pravděpodobnost náhodného jevu, že náhodně zakoupený výrobek je první jakosti. Rovněž vypočtěte pravděpodobost, že zakoupený výrobek první jakosti je od prvního výrobce a pravděpodobnost, že je od druhého výrobce.
Náhodný jev, zakoupení výrobku první jakosti si označíme písmenem A. Hypotézu, že je od prvního výrobce, si označíme H1, podobně H2 si označíme hypotézu, že je od druhého výrobce. Pravděpodobnost jevu A si spočteme podle věty o úplné pravděpodobnosti, viz obrázek č. 1a. Pravděpodobnost jevu A nám vyšla 0,75. Budiž. Všimněme si, že pravděpodobnost zakoupení výrobku první jakosti od prvního výrobce nám poklesla z 25 % na 22,5 %, podobně u druhého z 75 % na 52,5 %. Proč? Protože při výpočtu úplné pravděpodobnosti neuvažujeme všechy výrobky, ale pouze první jakosti. V dalším si podle Bayesova vzorce spočteme pravěpodobnosti P(H1|A) a P(H2|A). Vidíme, že zde nastal částečně opačný úkaz. P(H1|A) je 30 %, tedy vyšší než 25 %. Proč? První výrobce dodává 90 % výrobků první jakosti na rozdíl od druhého, který dodává jenom 70 % výrobků v první jakosti, takže pokud jsem si koupil výrobek první jakosti pravděpodobnost, že je od prvního výrobce se zvýší oproti původním 25 % na 30 %. P(H2|A) nám vyšlo 70 %, což je pokles oproti původním 75 %. Proč? Protože druhý výrobce dodává na rozdíl od prvního výrobce pouze 70 % výrobků v první jakosti. Na obrázku jsou sa konci uvedeny i kontrolní výpočty. Takhle nějak kvalitativně si je potřeba analyzovat každý výpočet. Nedoporučuji jenom spočíst výsledek, je vždy prospěšné pokusit se výsledek zdůvodnit i selskou úvahou.

Teď společně vyřešíme druhý ukázkový příklad. Je převzatý z výše uvedeného titulu autorů B. V. Gnedenka a A. Ja. Chinčina. a ten již typický bayseovský je. Tento příklad doporučuji zvládnout více než dobře, pokud jej pochopíte, pochopili jste celou bayesovskou teorii pravděpodobnosti. Při řešení sledujte obrázek č. 1b.
Jsme dělostřelci ne dělostreleckém cvičení. Cíl, který máme zasáhnout, leží v úseku ZK. Rafinovanost cvičné střelby je v tom, že i když cíl v průběhu palby zasáhneme, nepoznáme to. Pouze po skončení celé palby se dozvíme, zda jsme cíl zasáhli nebo nezasáhli. Navíc neznáme přesnou polohu cíle, známe jenom pravděpodobnosti zasažení cíle pokud střely zasáhnou úseky H1 až H5, to jsou výchozí hypotézy, tedy před vlastní střelbou. Jelikož největší pravděpodobnost zasažení cíle je v úseku H3, tak mířit a pálit budeme právě na úsek H3. Jenomže nikdo není dokonalý, ani my. Část střel nedopadne do H3. Přesto se po ukončení střelby dozvíme, že cíl jsme zničili. Řídící cvičení nám sdělí přesné počty dopadlých střel po úsecích, z čehož lehce odvodíme pravděpodobnosti zásahu cíle při praktické střelbě. Vidíme, že tyhle pravděpodobnosti se liší od původně zadaných pravděpodobností. Napadne nás na základě dosažených výsledku střelby původní pravděpodobnosti zasažení cíle v jednotlivých úsecích opravit. Jaké budou opravené pravděpodobnosti? Počítáme na 4 desetinná místa.
Při výpočtu si celou situaci názorně představíme. Počátečné pravděpodobnosti zasažení cíle jsou ze zadání jasné, takže se budeme snažit zasáhnout úsek H3. Představme si, že z děla jsme vypálili 100 střel (klidně jsem mohli zvolit jiné číslo, ale takhle se nám bude dobže počítat). Jak naše úspěšná střelba (bylo nám sděleno, že cíl jsme zasáhli) skončila, vidíme na obrázku. V úseku H1 skončili 2 střely, v úseku H2 16 střel atd. Když vypálené střely spočteme, zjistíme že v úseku ZK skončilo 98 střel, 2 střely dopadly mimo úsek ZK. V každém případě jsme z praktické střelby vytěžili novou zkušenost, ta je popsaná pravědpodobnostmi P(T|H1) až P(T|H5). A právě tuhle zkušenost využijeme k tomu, abychom původní pravděpodobnosti (hypotézy) opravili. To by mělo být cílem a smyslem aplikování bayesovské teorie. Zkušenost využít pro opravu původních pravděpodobností (hypotéz)! Je zřejmé, že tento proces zpřesňování odhadu může pokračovat. Praxí získáme nové poznatky a na jejich základě provedeme opravu momentálně platných pravděpodobností (hypotéz).
Ale opatrně. Musíme si dobře uvědomit, že pokud pravděpodobnosti (hypotézy) P(H1) až P(H5) nejsou známé nebo je odhadujeme jenom tak od oka, celý zde uvedený postup je k ničemu, protože vaříme z vody. A ještě další skutečnost, v případě, že nastane sledovaný jev (zde trefa cíle) musíme umět určit P(T|H1) až P(T|H5). V našem příkladu to problém nebyl, jednoduše jsme zjistili, kam dopadli námi vypálené náboje, ale kupříkladu v medicínské praxi to až tak jednoduché a jednoznačné nemusí být. Z toho plyne, že aplikování Bayesova přístupu musí předcházet důkladná kritická analýza problému, protože mechanické použití vzorečků je spolehlivou cestou k získání zcela zavádějících výsledků.
Výsledný výpočet s použitím Bayesova vzorce je zřejmý o obrázku. Pochopitelně námi navržené pravděpodobnosti musí dát sumárně číslo 1, jelikož cíl leží v úseku ZK. Vidíme, že tomu tak, po nezbytném zaokrouhlení, opravdu je.

A teď konečně dva slíbené příklady ze Sbírky na Bayesův vzorec.
Sbírka 7.1. Mějme deset stejných uren. V devíti z nich je po dvou černých a dvou bílých koulích, v jedné je pět bílých a jedna černá koule. Z náhodně zvolené urny byla vytažena bílá koule. Jaká je pravděpodobnost toho, že koule byla vytažena z urny, která obsahuje pět bílých koulí.
Řešení je na obrázku č. 2. Jedinou novinkou oproti příkladu se zmetky výrobků je, že nakonec použijeme Bayesův vzorec. Teď si dáme raději něco těžšího, půjdeme lovit divokého kance.
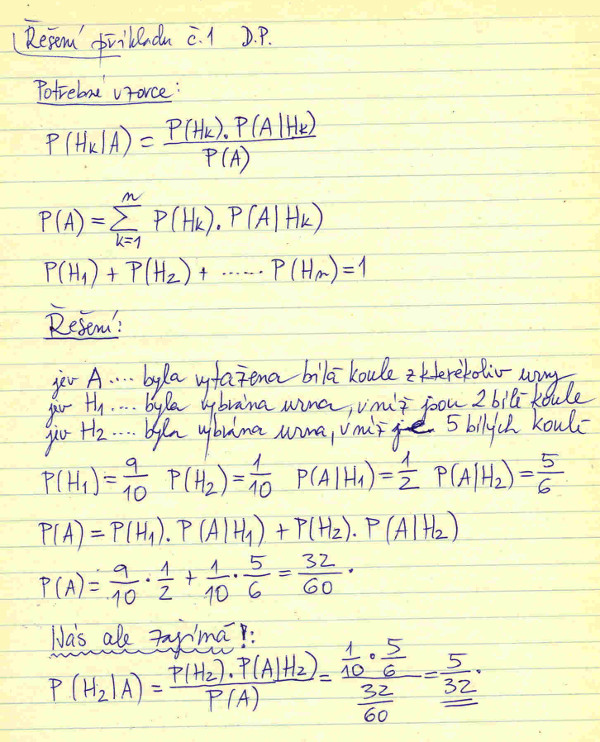
Sbírka 7.9. Teď vyrazíme na lov divokého kance, který byl jednou jedinou střelou zastřelen. Lovci jsou tři. Máme určit pravděpodobnost, že kance zastřelil první, druhý nebo třetí lovec, jsou-li pravděpodobnosti zásahu jednotlivými střelci: 0,2; 0,4; 0,6.
Řešení je na obrázku č. 3. Příklad je docela fikaný, nakonec proto jsem jej schválně vybral. Jako tradičně je důležité správně a jasně popsat výchozí situaci a příslušné jevy, což je největší problém v počtářské praxi, tedy nejen v ní, ale s tím si my jistě hravě zvládneme. Nejprve musíme spočíst pravděpodobnosti jednotlivých hypotéz P(Hk). Jak spočteme P(H1)? Použijeme větu o násobení pravděpodobnosti. Víme, že kance zasáhla jenom jedna jediná střela. V hypotéze H1 předpokládáme, že to byla střela vypálená prvním lovcem, další dva pálili vedle. Konkrétní výpočet těchto pravděpodobností je vidět na obrázku. Čárka nad pravděpodobností značí, že k-tý střelec se netrefil. To je sice hezké, ale teorie požaduje, aby součet pravděpodobností těchto hypotéz byl roven 1, tedy aby hypotézy H1, H2, H3 tvořily úplný systém jevů, tj. součet jejich pravděpodobností musí dát 1. Ale v našem výpočtu součet pravděpodobnosti těchto hypotéz nedává 1! Neuvažujeme nesprávně? Ne! V praxi se klidně mohlo stát, že se netrefil ani jeden střelec, vždyť pravděpodobnosti tref jsou po řadě pouze 0,2; 0,4; 0,6! Nakonec pravděpodobnost před střelbou, že divoký kanec bude zastřelen jednou jedinou ranou je pouze 0,464, tedy ani ne 50 %! Pokud vám přesto úplný systém jevů chybí, spočtěte si všechny možné pravděpodobnosti před střelbou, tj. že kanec nebyl trefen, byl trefen jednou ranou, dvěma a třemi. Suma vám musí vyjít 1, jelikož to jsou všechny možnosti před střelbou! My ale pracujeme s dodatečnou informací: víme, že kanec zastřelen byl jedinou ranou, takže jeden střelec se trefit musel, právě tahle dodatečná informace nás oprávňuje spočíst pravděpodobnosti jednotlivých hypotéz, tak jak jsme je spočetli a nakonec použít pro výpočty Bayesův vzorec! Pro jeho použití potřebujeme ještě znát P(A|Hk). Zkusme si tento formální zápis říct pěkně nahlas, např. pro prvního střelce: Jaká je pravděpodobnost zastřelení kance, pokud kance trefil první lovec? Přece 1, vždyť víme, že kanec byl zabit jenom jednou jedinou střela! Použití Bayesova vzorce je zřejmé z obrázku. P(Hk|A) jsou pravděpodobnosti, které jsme měli spočíst.

Na závěr nás čeká problém Montyho Halla, někdy se mluví o paradoxu. Proč, to za chvíli poznáme. Název paradoxu je podle jména amerického moderátora, který kdysi uváděl velice oblíbenou soutěžní show. Pokud si do google.com zadáte heslo monty hall, objeví se vám řada odkazů, kde je problém popsán a uvedeno několik řešení. O co vlastně jde?
Soutěžní cenou je auto, které moderátor umístil za jedny ze tří zavřených dveří. Za dalšími dvěma dveřmi není nic (v show pro efekt koza). V prvním kroku je úkolem soutěžícího zvolit si jedny dveře, ukázat na ně prstem, ale zatím je nesmí otevřít. V druhém kroku moderátor otevře jedny ze dvou zbývajících dveří, ale ty, za nimiž auto není, protože jinak by soutěž neměla smysl. V třetím kroku má soutěžící možnost buď setrvat na své původní volbě dveří, nebo volbu změnit na druhé neotevřené dveře, které mu doporučí moderátor. V úplném závěru se otevřou ty dveře, pro které se soutěžící nakonec rozhodl. Pokud se trefí, vyhrává auto. Soutěžící nemá žádné předchozí znalosti o tom, co je za dveřmi.
Naše první úvaha by mohla být následující. Na počátku hry je pravděpodobnost výhry auta podle klasického vzorce 1/3, protože máme troje stejných dveří a je stejná šance, že auto je za jedněmi z nich, jenomže háček je v tom, že i když soutěžící ukáže na správné dveře, tedy dveře, za nimiž auto je, dveře se zatím neotevřou a on vlastně neví, na čem je. Poté co moderátor jedny dveře otevře zůstanou neotevřeny dvoje dveří: na které ukazuje soutěžící a dveře, které neotevřel moderátor. Jako soutěžící mohu zvolit pouze jedny dveře ze dvou, takže pravděpodobnost je 1/2. Určitě je to lepší varianta, než se rozhodovat mezi třemi dveřmi. Otázkou ale je, zda šance soutěžícího na výhru auta je opravdu jenom 1/2? Co když je větší poté, co poslechne moderátora a nebude trvat na otevření dveří, na které ukázal na začátku hry? Je tomu opravdu tak?
Nechť naše výchozí situace je např. následující: soutěžící zvolí dveře číslo 1, které zatím zůstavají zavřené. Moderátor otevře dveře číslo 3, za nimiž auto není a nabídne soutěžícímu otevřít dveře číslo 2, za nimiž auto je, ale to pochopitelně soutěžící může jenom hádat, jistě to neví. Problém v této situaci zní: Zvýší se šance na výhru auta z 1/2 na nějaké větší číslo, pokud soutěžící moderátora poslechne a změní původní volbu z dveří č.1 na dveře číslo 2?
Podívejme se pozorně na časovou posloupnost jevů, jelikož bayesovská teorie pravděpodobnosti tuhle posloupnost zohledňuje, viz obrázek č. 4. Označení a popis jevů je je snad zřejmý. Jasné jsou i výchozí pravděpodobnosti. Náš problém zní: je P(A2|H3) větší než 1/2?

Abychom mohli použít Bayesův vzorec potřebujeme znát P(H3|A2) a P(H3). P(H3|A2) je 1. Proč? Pokud je auto za dveřmi č. 2 a soutěžící ukazuje na dveře č. 1, tak moderátor nemá jinou volbu, než otevřít dveře č. 3. K výpočtu P(H3) použijeme větu pro úplnou pravděpodobnost. Abychom ji mohli použít, potřebujeme znát P(H3|A1) a P(H3|A3). P(H3|A1) je 1/2. Proč? Pokud auto je za dveřmi č.1, moderátor může otevřít dveře č. 2 nebo č. 3, tedy má na výběr dvě rovnocenné možnosti. P(H3|A3) je 0. Proč? Pokud je auto za dveřmi č. 3, moderátor dveře č. 3 nemůže podle pravidel hry otevřít. Pravděpodobnost P(A2|H3) nám vyšla po dosazení do Bayesova vzorce 2/3, což je pravděpodobnost větší nejen oproti výchozí pravděpodobnosti 1/3, ale i oproti pravděpodobnosti 1/2 po otevření dveří moderátorem. Pokud soutěžící chce zvýšit dvoji šanci na výhru auta, měl by doporučení moderátora na otevření dveří č. 2 poslechnout.
Je otázkou, zda na výsledek 2/3 nelze dojít i prostou úvahou bez výše uvedeného, relativně složitého, výpočtu. Zkusme to. Představme si, že auto je za dveřmi č. 1, za dveřmi č. 2 a č. 3 je pokaždé kozel. Z pohledu soutěžícího jsou celkem tři možnosti. 1. možnost je, že vybere dveře č. 1, moderátor otevře dveře č. 2 nebo č. 3 a nabídne mu k otevření dveře č. 3 nebo č. 2. Soutěžící moderátora poslechne a ... prohrál. 2. možnost je, že soutěžící vybere dveře č. 2, moderátor otevře dveře č. 3 a nabídne soutěžícímu k otevření dveře č. 1. Ten poslechne a vyhraje. 3. možnost je, že soutěžící ukáže na dveře č. 3, moderátor otevře dveře č. 2 a nabídne k otevření dveře č. 1. Soutěžící poslechne a vyhrál. Vidíme, že pokud soutěžící pokaždé moderátora poslechne, tak jeho šance na výhru jsou 2/3.
Jenomže buďme realisti, i kdyby soutěžící nakonec auto vyhrál, v životě nemusí mít vyhráno. Už jenom z toho důvodu, že v euforické náladě při jízdě domů může havarovat a zabít se. Podobně jako se zabil Mario (hrál ho Yves Montand) ve filmu Mzda strachu z roku 1953. Vydělal podstoupením obrovského rizika veliké peníze a jel za svou milou, aby si s ní užil lásky i bohatství. Leč nedojel.
V Brně 1. července 2015.
Doplněk ze dne 26. července 2015. Napsal mi čtenář, že má knihu: Amir D. Aczel: Náhoda (Dokořán, Praha, 2008) a že v knize jsou cvičení a k ním výsledky. Rovněž je tam příklad na Bayesovu větu, jenomže výsledek jeho řešení není v souladu s výsledkem, který je v knize uveden. Svůj výsledek ani postup řešení mi nesdělil, jenom mě požádal, zda bych se nemohl pokusit příklad vyřešit. Knihu mi dcera půjčila v knihovně. Ani moje řešení není v souladu s autorem uvedeným řešením. Podle autora správné řešení je 105/439, tedy 0,239. Mně vyšlo 0,249. Tak nevím? Autorovi jsem své řešení poslal, jenomže nevím, zda adresu vyhledanou přes Google ještě používá. Níže je uvedeno zadání příkladu i mé řešení. Značení dodržuji jako u výše uvedených příkladů.
V domě se nachází pět bytů. V jednom žijí dva muži, v jednom žena a tři muži, v jednom dvě ženy a tři muži, v dalším šest žen a jeden muž a v posledním žije manželský pár. Jestliže zaklepeme na dveře a otevře žena, s jakou pravděpodobností stojíme u bytu, v němž žije manželský pár.
Při řešení jsem vyšel z předpokladu, že pokud zaklepeme na dveře manželského páru, pravděpodobnost toho, že dveře otevře žena je 1/2. Se stejnou pravděpodobností dveře může otevřít manžel.
