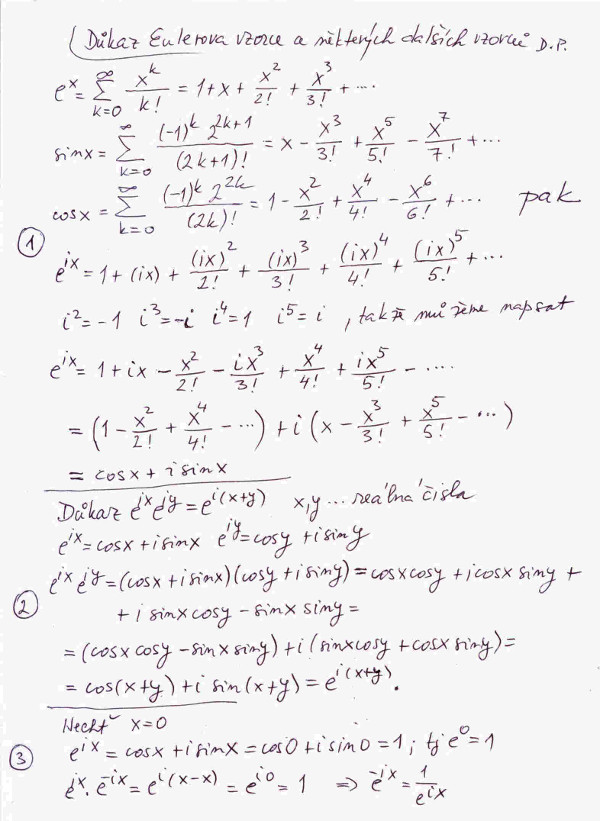Je rovnice cos z = 5 řešitelná?
Dušan Polanský
S velikou pravděpodobností si asi v duchu pomyslíte, že tahle rovnice vypadá nějak divně, vždyť i žák deváté třídy Základní školy (za nás Základní devítileté školy) ví, že funkce kosinus má obor funkčních hodnot od -1 do +1, tak jak může být na pravé straně číslo 5?! Přece není takový úhel, aby jeho kosinus byl 5! Pravda to sice je, ale má to háček, na Základní škole žáci pracují pouze s reálnými čísly. K těm se dopracují postupně, začínají s přirozenými čísly, pak postoupí k číslům racionálním (zlomky), pak poznají svět záporných čísel, čímž se jim otevřou dveře k číslům celým a až nakonec poznahí čísla reálná. Svět reálných čísel je opravdu velice bohatý a pestrý, a dokonce dodnes ne zcela prozkoumaný, takže jeden by si mohl pomyslet, že s reálnými čísly bychom mohli vystačit i pro řešení zmíněné rovnice. Bohužel nevystačíme už jenom proto, že trigonometrická funkce kosinus v reálném oboru je definovaná tak, že zmíněná rovnice jednoduše řešení nemá.
S naším povídáním souvisí i jeden dost zásadní matematický problém. Jistě si ze základky pamatujete, že řešení rovnice x2 = 4 nedělá zvláštní problém: řešením jsou čísla 2 a –2. Ovšem s řešením jenom kapánek pozměněné rovnice x2 = – 4 už problém máme, a to dokonce principiální. Jednoduše nemáme po ruce taková dvě reálná čísla, že jejich umocněním dostaneme – 4. Aby se řešení téhle jednoduché rovnice našlo, museli matematici obohatit (rozšířit) svět reálných čísel o další (komplexnější) čísla, které budou obsahovat reálná čísla coby svou podmnožinu. Takovými čísly jsou čísla komplexní. Jsou ještě čísla komplexnější, např. kvaterniony, ale ty k řešení rovnice cos z = 5 nebudeme potřebovat.
Rozšíření reálných čísel přitom vychází z docela jednoduché úvahy: musíme k odmocnině z absolutní hodnoty na pravé straně rovnice (v našem příkladu k odmocnině z čísla 4) přifařit něco takového, co velikost odmocniny nezmění, ale při umocnění na druhou to dá znaménko –. A tak přišla na svět imaginární jednotka i. Její zcela fundamentální a nekompromisně požadovaná vlastnost je, že i.i = –1. Pak již zbýval jenom malý krůček k zavedení komplexního čísla: a + ib, kde a, b jsou reálná čísla. Popravdě historicky to proběhlo kapánek složitější a trvalo to déle, ale to nás trápit nemusí. Znáte to, po válce je každý generál.
A div se mi světe, pokud z bude komplexní proměnná, rovnice cos z = 5 má v oboru komplexních čísel řešení, o čemž se za chvíli přesvědčíme. Jinak označení z jsme použili proto, že ve světě komplexních čísel se komplexní proměnná obvykle značí z. Na Základní škole jsme (reálnou) neznámou obvykle značili x, v případě dvou rovnic o dvou (reálných) neznámých x a y. V matematice sice platí, že si neznámou můžeme označit víceméně jako chceme, jenom musíme uvést, jaký je její definiční obor. Ovšem i v matematice většinou platí, že zvyk je železná košile, a proto i my se budeme v případě komplexní proměnné držet označení z.
Pokud jde o znalosti potřebné k pochopení hlavního textu, bohatě vystačíme se základními poznatky o komplexních číslech (de facto s definicí komplexního čísla), dále se znalostmi trigonometrie na úrovni Základní školy, dále předpokládáme, že víme, jak je definován logaritmus se základem e, a umíme vyřešit kvadratickou rovnici s kladným diskriminantem. V dodatku je, mimo jiné, uveden důkaz Eulerova vzorce. Důkaz předpokládá znalost pojmu nekonečná řada. Eulerův vzorec mnozí matematici považují se nejkrásnější vzorec celé matematiky, popravdě ani se tomu moc nedivím, vždyť propojuje v jedno svět komplexních a reálných čísel. Nakonec i my tento vzorec v dalším naplno využijeme. Pochopení důkazů uvedených v dodatku není nezbytné k pochopení hlavního textu. Vše potřebné k pochopení řešení rovnice cos z = 5 je uvedeno v hlavním textu.
Na obrázku č. 1 (číslo zjistíte, po najetí kurzoru myši na obrázek) je uvedena definice komplexního čísla a je uvedeno výsledné řešení rovnice z2 = a, kde a je libovolné reálné číslo, tedy i zmíněné rovnice z2 = – 4. Lze říct, že na tomto obrázku je jakési mini opáčko o komplexních číslech, přesněji jejich lehké připomenutí.

Na obrázku č. 2 při výpočtech využíváme naplno Eulerův vzorec a platnost vztahu pro komplexní proměnnou: ea+b = eaeb, kde e je Eulerovo číslo a a b jsou komplexní proměnné. Důkaz Eulerova vzorce je pro zvídavější čtenáře uveden v příloze. V příloze je rovněž uveden s určitým zjednodušením důkaz vztahu ea+b = eaeb. Zjednodušení spočívá v tom, že uvažujeme jenom imaginární část komplexních čísel, což ale stále komplexní čísla jsou. Důkaz i s reálnou částí komplexního čísla se dělá obvykle pomocí nekonečných řad, ale ten se mi zdál trochu složitý, tak jsem jej vypustil. Na tomto obrázku dále naleznete připomenutí definice logaritmu. Následně je za pomoci Eulerova vzorce dokázáno, že komplexní mocnina má jistou periodu. Výsledně je zde odvozen vztah pro přirozený logaritmus komplexní proměnné. Pro větší názornost jsou uvedeny dva jednoduché příklady na výpočet přirozeného logaritmu.

Konečně máme připraven nezbytný matematický aparát pro vyřešení rovnice cos z = 5. Výpočet je podán podrobně na obrázku č. 3. Věřím, že pozorný čtenář nebude mít s výpočtem potíže. Vidíme že úhel, pro který je kosinus z roven 5, nám vyšel ve velice rafinované podobě, je to imaginární číslo, což by nás ale nemělo překvapit, jelikož víme, že v oboru reálných čísel naše rovnice řešení nemá. A ve výsledném vzorečku jaksi nemůže chybět ani naše imaginární jednotka i, a také že tam je. Nakonec z, které vyhovují rovnici je nekonečně mnoho, to proto, že n ve výsledném vzorci je libovolné celé číslo.

Těsně před závěrem dodejme, že ačkoliv komplexní čísla působí na nás tak trochu virtuálně, tedy neskutečně, jejich uplatnění v matematice a jejich různých praktických aplikacích, např. ve fyzice, elektrotechnice, je značné a velice pestré. Snad vás tento lehce matematický napsaný text laika kapánek navnadil k tomu, abyste se o svět komplexní proměnné začali více zajímat. Pokud se tak stane, cíl textu byl splněn.
Pokud jde o matematiku jako takovou nemají to dnes středoškoláci jednoduché. Matematici se snaží prosadit zavedení povinné maturity z matematiky, prostě cítí příležitost, jak se zviditelnit a udělat důležitými, přitom jiní vědci nám zase tvrdí, že současné století už je a bude stoletím chemie a biologie. Jazykáři zase tvrdí, že znalost cizích jazyků nebyla nikdy tak důležitá, jako právě dnes, kdy je celý svět výrobně, dopravně a komunikačně úzce propojen. Holt středoškoláci to nemají dnes vůbec lehké, ještě štěstí že už jsem v důchodu. Pokud vás zajímá můj názor na pokus o zavedení matematiky coby povinného maturitního předmětu je k přečtení zde. A to je vše.
V Brně 14. února 2020.